数制转换
将十进制数N转换为r进制的数,其转换方法利用辗转相除法:以N=3467,r=8为例转换方法如下:
代码如下:(这里我们省略了对于栈实现的代码若需要查看栈的内部代码请看:栈和队列)
int main(){
SqStack s;
InitStack(&s);
int N,r;
cin >> N >>r;
while(N>0)
{
Push(&s,N%r);
N/=r;
}
cout << "N的r进制为:";
while(!StackEmpty(s))
{
int e;
Pop(&s,&e);
cout << e ;
}
cout <<endl;
return 0;
}运行结果如下:
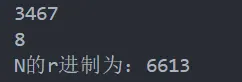
由于没有做高于10进制数的对于字母的映射,所以该程序最多只能支持转为比10更低的进制。
括弧匹配检验
假设表达式中允许包含两种括号:圆括号和方括号,其嵌套的顺序随意,如([]())或[([ ][ ])]等为正确的匹配,[( ])或([ ]( )或 ( ( ) ) )均为错误的匹配。
代码如下:
int main(){
SqStack s;
InitStack(&s);
char brackets[100];
cin >> brackets;
int i = 0;
while(brackets[i] == '[' || brackets[i] == '(' || brackets[i] == ']' || brackets[i] == ')')
{
if(brackets[i] == '[' || brackets[i] == '(' )
{
Push(&s,brackets[i]);
}
else
{
char tmp;
if(StackEmpty(s))
{
cout << "不匹配!" << endl;
break;
}
Pop(&s,&tmp);
if(brackets[i] == ']' && tmp == '(')
{
cout << "不匹配!" << endl;
break;
}
else if(brackets[i] == ')' && tmp == '[')
{
cout << "不匹配!" << endl;
break;
}
}
i++;
}
if(!StackEmpty(s))
{
cout << "不匹配!" << endl;
}
if(brackets[i] == '\0')
{
cout << "匹配成功!" << endl;
}
return 0;
}运行结果如下:
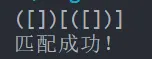
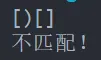
博主不一定保证一定正确。
三种表达式
虽说是三种表达式,但是本篇只讲解中缀表达式和后缀表达式。本blog展示的代码都只能计算单个数字的表达式。
后缀表达式
运算符在式中出现的顺序恰为表达式的运算顺序;每个运算符和在它之前出现且紧靠它的两个操作数构成一个最小表达式。
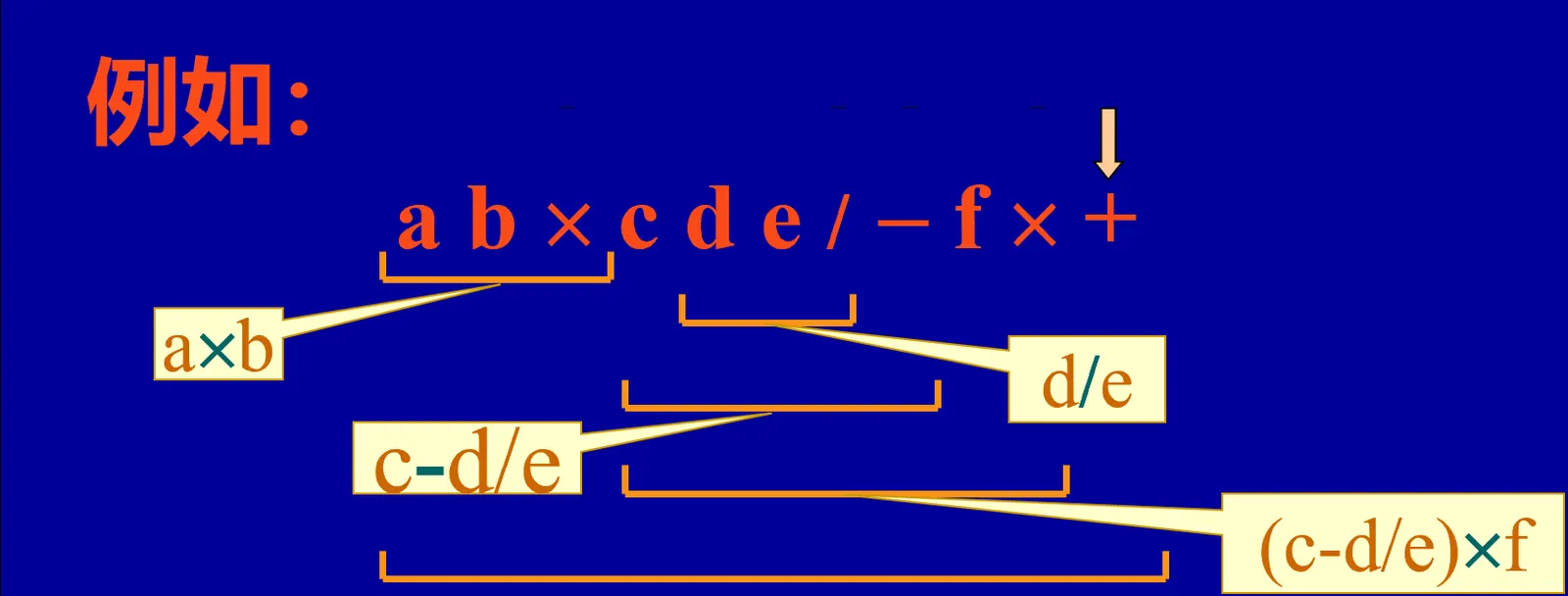
计算后缀表达式,代码如下:
int main(){
SqStack s;
InitStack(&s);
char str[100];
cin.getline(str, 100);
int i = 0;
while(str[i] != '\0')
{
if(str[i] == '+' || str[i] == '-' || str[i] == '*' || str[i] == '/')
{
int x,y,res;
Pop(&s,&y),Pop(&s,&x);
if(str[i] == '+')
res = x+y;
else if(str[i] == '-')
res = x-y;
else if(str[i] == '*')
res = x*y;
else if(str[i] == '/')
res = x/y;
Push(&s,res);
}
else if(str[i] >= '0' && str[i] <= '9')
{
Push(&s,str[i]-'0');
}
i++;
}
int e;
Pop(&s,&e);
cout << "计算结果为:"<< e <<endl;
return 0;
}中缀表达式转后缀表达式
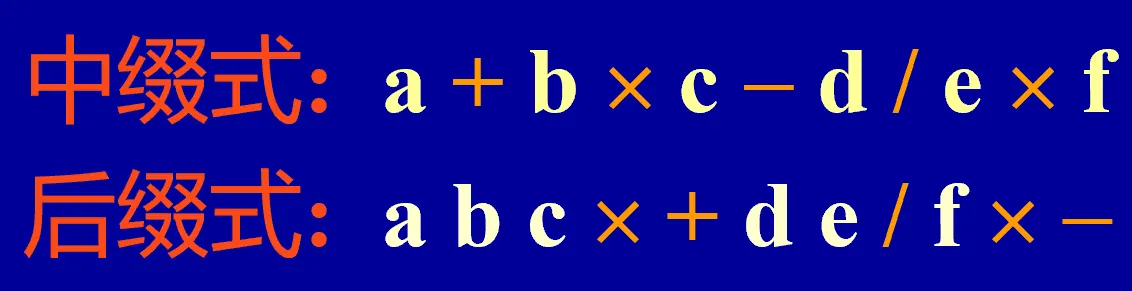
对于这种没有括号的中缀表达式,我们给出以下解法:
int main(){
SqStack s;
char str[100],e;
cin.getline(str,100);
InitStack(&s);
Push(&s,'#');
int i = 0;
while(str[i] != '\0')
{
char tmp = str[i];
if(tmp <= '9' && tmp >= '0')
{
cout << tmp;
}
else if(tmp == '+' || tmp == '-' || tmp == '*' || tmp == '/')
{
GetTop(s,&e);
if(tmp == '*' ||tmp == '/')
{
while(e != '#' && e!= '+' && e!='-')
{
Pop(&s,&e);
cout <<e;
GetTop(s,&e);
}
}
if(tmp == '+' ||tmp == '-')
{
while(e != '#')
{
Pop(&s,&e);
cout <<e;
GetTop(s,&e);
}
}
Push(&s,tmp);
}
i++;
}
GetTop(s,&e);
while(e != '#')
{
Pop(&s,&e);
cout <<e;
GetTop(s,&e);
}
return 0;
}我们遵守以下几点运算规则:
- 通过栈来暂存运算符
- 设表达式的结束符为#,所以提前预设栈底元素为‘#’
- 当前字符若是数字,直接打印出来
- 若当前为运算符,则需要输出栈中所存的所有优先级大于等于它的运算符
- 然后让当前元素进栈
- 读取到字符串末尾,将所有元素出栈
而增加了括号后,我们将括号视作一种隔绝作用,在一个”(“遇到对应的“)”相消之前,我们认为”(“就是栈低,对于括号之下的数据暂不输出。并且在读到“)“时,我们应该将量括号间的符号全部输出出去。
但是对于其他规则,都是一致的。完善后的代码如下:
int main(){
SqStack s;
char str[100],e;
cin.getline(str,100);
InitStack(&s);
Push(&s,'#');
int i = 0;
while(str[i] != '\0')
{
char tmp = str[i];
GetTop(s,&e);
if(tmp <= '9' && tmp >= '0')
{
cout << tmp;
}
else if(tmp == '+' || tmp == '-' || tmp == '*' || tmp == '/' || tmp == '(')
{
if(tmp == '*' ||tmp == '/')
{
while(e != '#' && e!= '+' && e!='-' && e != '(')
{
Pop(&s,&e);
cout <<e;
GetTop(s,&e);
}
}
if(tmp == '+' ||tmp == '-')
{
while(e != '#' && e != '(')
{
Pop(&s,&e);
cout <<e;
GetTop(s,&e);
}
}
Push(&s,tmp);
}
else if(tmp == ')')
{
while(1)
{
Pop(&s,&e);
if(e == '(')
break;
cout <<e;
}
}
else if(tmp == '#')
{
while(e != '#')
{
Pop(&s,&e);
if(e == '#')
break;
cout <<e;
}
}
i++;
}
return 0;
}我们只需要增加一处if用来处理读到’)‘时的反应,再将’(‘作为出栈时的一个触底条件即可。
中缀表达式求值
前面我们已经学会了中缀表达式转后缀表达式,那么对于中缀表达式求值,其实我们只需要替换一部分代码,就可以直接得到中缀表达式求值的代码
- 将所有打印数字的代码替代为将数字压入数字栈
- 将所有打印运算符号的代码改为从栈中出栈两个数据做原本打印符号的运算再将结果入栈
- 最后我们输出栈顶元素就是运算的结果
我们就得到以下代码:
int main(){
SqStack s,n;
InitStack(&s);
InitStack(&n);
char str[100],e;
cin.getline(str,100);
Push(&s,'#');
int i = 0;
while(str[i] != '\0')
{
char tmp = str[i];
GetTop(s,&e);
if(tmp <= '9' && tmp >= '0')
{
Push(&n,tmp-'0');
}
else if(tmp == '+' || tmp == '-' || tmp == '*' || tmp == '/' || tmp == '(')
{
if(tmp == '*' ||tmp == '/')
{
while(e != '#' && e!= '+' && e!='-' && e != '(')
{
Pop(&s,&e);
char n1,n2;
Pop(&n,&n1),Pop(&n,&n2);
if(e == '*')
{
n1 = n1 * n2;
}
else if(e == '/')
{
n1 = n2/n1;
}
Push(&n,n1);
GetTop(s,&e);
}
}
if(tmp == '+' ||tmp == '-')
{
while(e != '#' && e != '(')
{
Pop(&s,&e);
char n1,n2;
Pop(&n,&n1),Pop(&n,&n2);
if(e == '*')
{
n1 = n1 * n2;
}
else if(e == '/')
{
n1 = n2/n1;
}
else if(e == '+')
{
n1 = n1 + n2;
}
else if(e == '-')
{
n1 = n2 -n1;
}
Push(&n,n1);
GetTop(s,&e);
}
}
Push(&s,tmp);
}
else if(tmp == ')')
{
while(1)
{
Pop(&s,&e);
if(e == '(')
break;
char n1,n2;
Pop(&n,&n1),Pop(&n,&n2);
if(e == '*')
{
n1 = n1 * n2;
}
else if(e == '/')
{
n1 = n2/n1;
}
else if(e == '+')
{
n1 = n1 + n2;
}
else if(e == '-')
{
n1 = n2 -n1;
}
Push(&n,n1);
}
}
else if(tmp == '#')
{
while(e != '#')
{
Pop(&s,&e);
if(e == '#')
break;
char n1,n2;
Pop(&n,&n1),Pop(&n,&n2);
if(e == '*')
{
n1 = n1 * n2;
}
else if(e == '/')
{
n1 = n2/n1;
}
else if(e == '+')
{
n1 = n1 + n2;
}
else if(e == '-')
{
n1 = n2 -n1;
}
Push(&n,n1);
}
}
i++;
}
char v;
Pop(&n,&v);
cout << int(v) << endl;
return 0;
}