每日一言

Look around you, and all you will see are people the world would be better off without. — Light Yagami from Death Note

外存信息的存取

外部排序的基本方法——归并排序法

步骤

生成若干初始归并段(初始归并串/顺串)，即对文件进行预处理
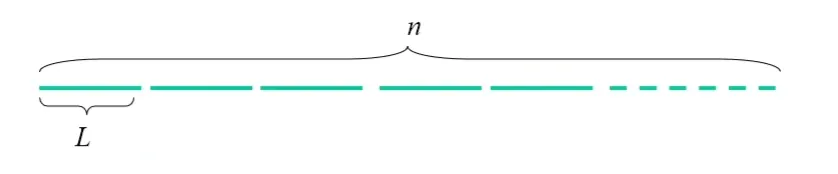
- 把含有n个记录的文件，按内存缓冲区大小分成若干长度为L的可一次完整装入内存的子文件/段；
- 将每个段，依次调入内存用有效的内排序方法排序后送回外存，形成若干个“初始归并段”；
对初始归并段进行多路合并(多路归并)

初始方法：对初始归并段进行多次2路归并排序，直至最后在外存上得到整个有序文件为止（原理同内排序的2路归并排序）

示例：

假设一次I/O的物理块大小为150，每次可对750 个记录进行内部排序，那么对含有150000个记录的磁盘文件进行4-路平衡归并排序时，共需进行多少次I/O？写出计算过程和结果。

1.初始归并段的生成：

每次内部排序可以处理750个记录。
总共有150000个记录。
因此，初始归并段的数量为：150000 / 750 = 200 段。

I/O次数的计算

每次I/O只能读取或写150个记录。
每段有750个记录，因此每段需要(750 / 150)*2 = 10次I/O来读写。

第一次归并：(200 / 4 = 50)

读200 段写200段，则读写10 * 200 = 2000次
第二次归并：(48/4+2/2 = 13)

读200 段写200段，读写10 * 200 = 2000次
第三次归并：(12/4 +1 = 4)

未进行全部的归并，按条数多的一段16*750 = 12000条未参加计算读写：10 * 200 - 160 = 1840 次
第四次归并：(4 /4 =1)

读200 段写200段，读写10 * 200 = 2000次

总读写次数：2000*4- 160 = 9840次

大多数情况下，我们可以通过公式： $\lceil \log_k m \rceil$ 直接计算k路归并要归并的次数，再乘以每次归并需要读写的次数算出大致I/O次数：

$\lceil\log_4 200 \rceil$ = 4

则I/0次数为：4 * 200 * (750/150) *2 = 10000次

多路(k路)平衡归并

设，记录总数为n，初始归并段的个数为m，进行k路归并合并，共进行 $s = \lceil \log_k m \rceil$ 趟归并。

胜者树

胜者树是一棵 完全二叉树 ，其每个内节点存储的是其两个子节点中的“胜者”（即较优值，如较小值或较大值）的索引，而叶子节点存储的是参赛者（归并段中的元素）的索引或值。

特点：

比较过程：
- 从叶子节点开始，依次将相邻两个参赛者进行比较，将“胜者”传递到父节点。
- 比赛从下到上，直到根节点，此时根节点存储的是整体的胜者（全局最优值）。
快速更新：
- 当一个叶子节点（归并段中的一个元素）发生变化时，只需重新比较该叶子节点所在路径的节点，大约需要 O(log k) 的时间。
应用场景：
- 用于多路归并中快速找到最小值（或最大值），并更新状态。
- 胜者树的时间复杂度通常为 O(n log k) ，其中 n 是数据总量，k 是参与归并的路数。

胜者树示例：

假设有 4 个归并段，当前数据如下：

归并段 1：[3, 7, 9]
归并段 2：[2, 8, 10]
归并段 3：[5, 6, 12]
归并段 4：[1, 4, 11]

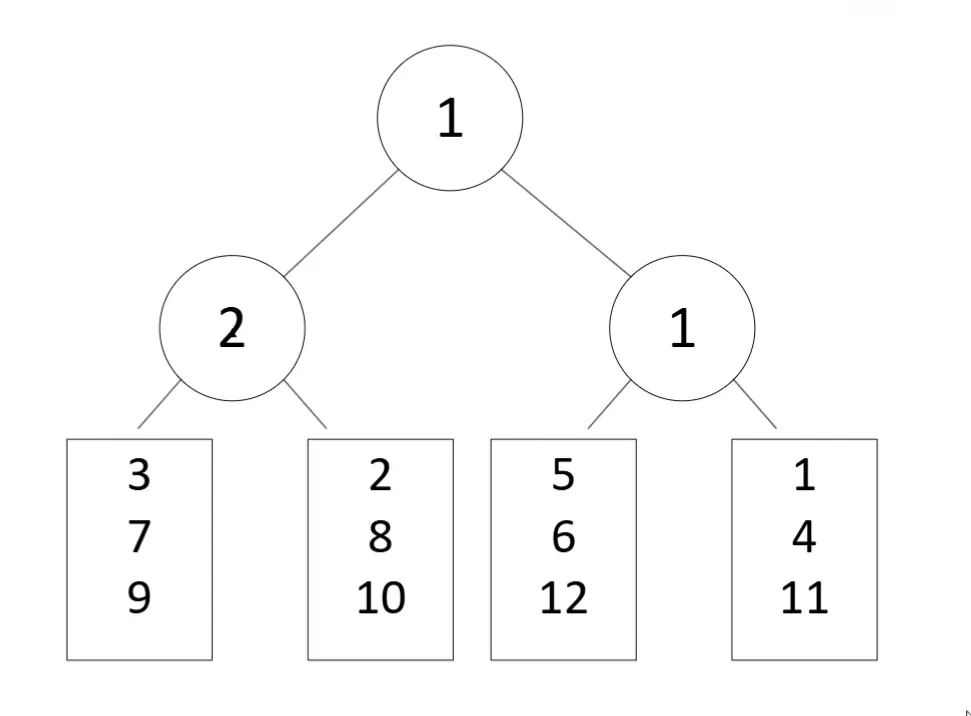
构建胜者树：

每个叶子节点表示 4 个段的当前最小值：[3, 2, 5, 1]
比较相邻叶子，产生胜者：
- 第一层比较：3 vs 2 -> 2，5 vs 1 -> 1
- 第二层比较：2 vs 1 -> 1（最终胜者）
最终，根节点为 1，即当前全局最小值。

更新过程：

如果叶子节点 1 被取走，下一个值为 4，更新路径上的父节点并重新比较。
更新只需 O(log k) 的时间。

1734333713368

败者树

败者树与胜者树类似，但其每个内节点存储的是比赛中的败者（即较差值，如较大值或较小值）的索引，而非胜者。最终的胜者存储在树的根节点之外。

特点：

比较过程：
- 与胜者树相同，从叶子节点开始比较，但每个父节点存储的是比赛中较差的一方（败者）。
- 根节点外部存储了全局的胜者。
快速更新：
- 更新时同样沿着路径重新比较，更新时间复杂度为 O(log k) 。
应用场景：
- 用于多路归并或多路选择问题，效果与胜者树相同，但实现中可以简化根节点的处理逻辑。

败者树示例：

同样的数据 [[3, 2, 5, 1]]：

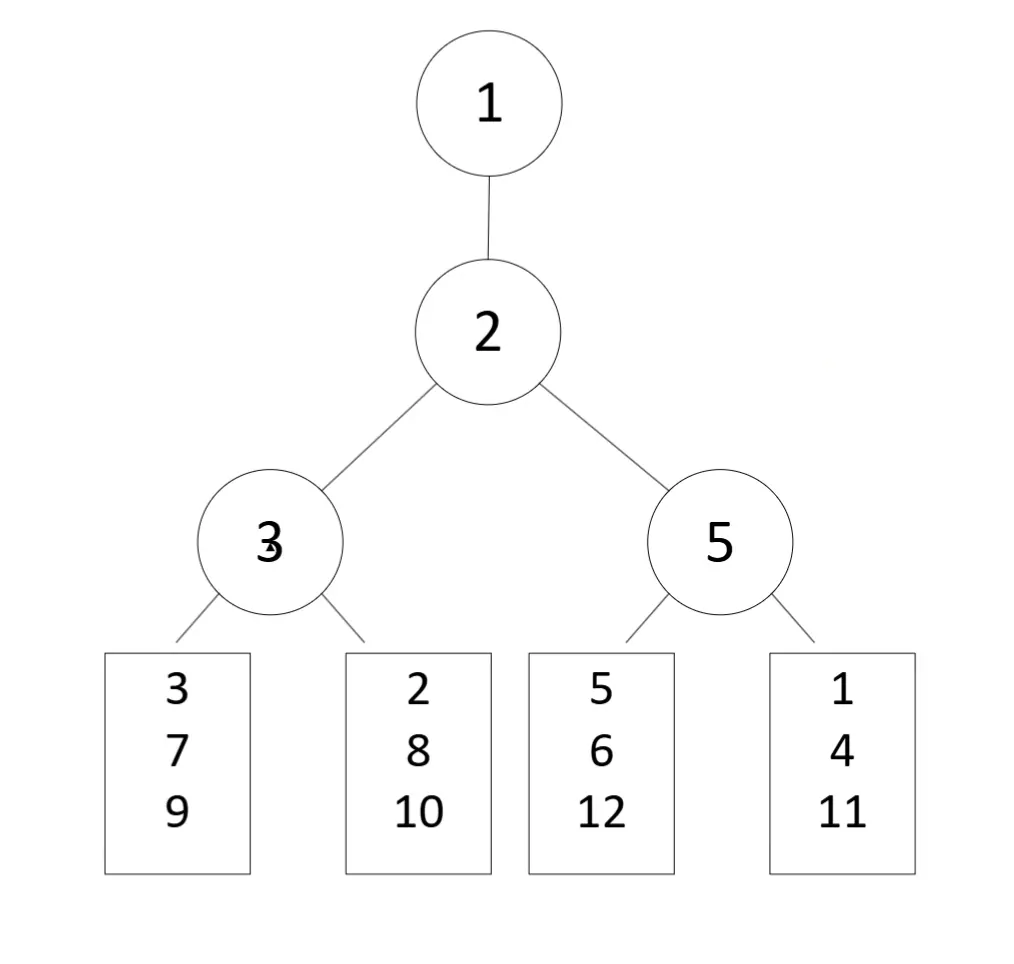
构建败者树：

每个叶子节点表示 4 个段的当前最小值：[3, 2, 5, 1]
比较相邻叶子，产生败者：
- 第一层比较：3 vs 2 -> 3（败者存父节点，2 继续比赛），5 vs 1 -> 5
- 第二层比较：2 vs 1 -> 2（败者存父节点，1 存为胜者）
根节点外存储全局胜者 1。

更新过程：

如果叶子节点 1 被取走，下一个值为 4，重新比较并更新路径。

1734333673404

但是在实际实现时，也可以选择不保存败者的实际数据，而是保存败者的归并段号，便于补充记录值。

胜者树 vs 败者树

特性	胜者树	败者树
内节点存储	胜者（较优值）	败者（较差值）
根节点	存储全局胜者	根节点外部存储全局胜者
构建复杂度	O(k log k)	O(k log k)
更新复杂度	O(log k)	O(log k)
实现复杂度	相对简单	稍复杂，根节点逻辑更清晰
适用场景	多路归并、快速找最优解	多路归并、快速找最优解

多路（k路）平衡归并

多路平衡归并是一种扩展的归并排序算法，它将数据划分为多个归并段（runs），在每一轮归并时， 同时处理k个归并段并将它们合并成一个有序段 。通过利用多路归并，可以减少归并轮数，从而提高外存排序的效率。

核心思想

初始归并段生成 ：将原始数据划分为若干个初始有序段（runs），每个段可以通过内存内排序（例如置换选择排序、快速排序等）生成。
多路归并 ：每次从k个归并段中选出最小（或最大）值，并将其输出到结果段中。重复此过程，直至所有段处理完毕。
递归归并 ：如果归并后的段数仍大于k，则需要进行多轮归并，直到所有数据归并为一个有序段。

关键步骤

1. 初始归并段的生成

数据分块 ：从外存中读取固定大小（等于内存容量）的数据块，使用内存排序算法将其排序成一个有序段（run）。
输出到外存 ：每处理一个块，将排序后的有序段存储到外存中，形成初始归并段。

2. 多路归并过程

多路归并的核心是 合并k个有序段 ，通常使用最小堆或优先队列优化归并效率。步骤如下：

初始化：从每个归并段中读取第一个记录，构建一个最小堆（按关键字排序）。
取堆顶元素（当前最小值）输出到结果段，并从对应段中读取下一条记录，更新堆。
重复以上过程，直到所有段的数据都输出完毕。

3. 递归归并

如果一次归并无法处理所有段，则归并k个段生成新的段，递归进行。
最终所有段被归并为一个整体有序段。

多路平衡归并的特点

减少归并轮数 ：如果是两路归并，每轮会将段数减少一半；而k路归并每轮可以将段数减少到1/k，显著减少轮数。
外存与内存交互 ：每次只读取固定大小的数据到内存，避免将所有数据加载到内存中。
时间复杂度 ：

总时间复杂度为 O(n logₖ m) ，其中：
- n 是数据总量；
- m 是初始归并段的数量；
- k 是归并的路数。

适用场景 ：

常用于外存排序、大规模数据处理（例如数据库的排序操作）。
特别适合内存有限、但可以利用外存的场景。

举例说明

假设有 16 个数需要排序，内存一次只能存放 4 个数，采用 4 路归并的过程如下：

1. 初始归并段的生成

将数据分为 4 段，分别排序成初始归并段：

原始数据：[20, 10, 15, 5, 30, 25, 35, 40, 50, 45, 60, 55, 70, 65, 75, 80]
初始段：[5, 10, 15, 20]，[25, 30, 35, 40]，[45, 50, 55, 60]，[65, 70, 75, 80]

2. 4 路归并

将 4 段归并为一个段：

从 4 个段中分别取第一个数，形成一个最小堆：
- 堆中初始值为 [5, 25, 45, 65]，堆顶为 5。
输出堆顶（5）到结果段，并从第一个段中读取下一个数（10），更新堆。
重复该过程，直至所有段合并为一个有序段。

结果：[5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80]

置换——选择排序

置换选择排序的基本步骤

初始化
- 将内存大小设为k，加载k个记录到内存。
- 选择k个记录中的最小关键字记录，记为 minimax，并将其输出到外存，形成初始归并段的一部分。
记录替换
- 当内存中空出一个位置时，从外存中补充一个新记录进入内存，保持内存中有k个记录。
- 在内存的k个记录中，寻找 大于 minimax的最小关键字 ：
  - 如果找到：将其输出到外存，更新 minimax为此记录的关键字。
  - 如果找不到（内存中的所有记录都小于 minimax）：生成一个完整的初始归并段。
新归并段生成
- 当一个归并段完成时，记录当前归并段，并重新开始：
  - 将当前内存中的所有记录清空并填充新的k个记录。
  - 重复上述步骤，继续生成归并段。
终止条件
- 当外存中的所有待处理记录都被读取并处理后，算法结束。

示例

假设有以下数据集合需要排序：[15, 21, 10, 8, 35, 19, 25, 5]，内存容量k=3。

过程：

初始内存加载 ：加载 [15, 21, 10]，找到最小值 10，输出到外存，更新 minimax = 10。
从外存补充新数据 8，内存为 [15, 21, 8]。
- 在内存中找到 大于 10的最小值 ：15，输出到外存，更新 minimax = 15。
补充新数据 35，内存为 [35, 21, 8]。
- 找到大于 15的最小值：21，输出到外存，更新 minimax = 21。
补充新数据 19，内存为 [35, 19, 8]。
- 找到大于 21的最小值：35，输出到外存，更新 minimax = 35。
补充新数据 25，内存为 [25, 19, 8]。
- 此时内存中所有值均小于 35，形成一个初始归并段 [10, 15, 21, 35]。
继续加载数据生成下一个归并段，直至所有记录处理完毕。

最终生成归并段：[10, 15, 21, 35] 和 [8, 19, 25, 5]。

采用败者树来实现置换-选择排序

败者树与置换-选择排序的关系

置换-选择排序的过程 ：

内存中维护一个大小为 k 的缓冲区存储记录。
每次从缓冲区中选出最小的记录输出到外存，然后用新的数据填充缓冲区。
当缓冲区中所有剩余记录的值都小于刚输出的记录时，当前归并段结束，开启新的一段。

败者树的作用 ：

快速找到缓冲区中的 最小值 （用于输出）。
高效更新缓冲区中的记录（用新值替代被选出的最小值）。
减少比较次数，将记录的维护复杂度从 O(k) 降低到 O(log k)。

置换-选择排序的实现步骤

1. 初始化

将内存大小设为 k，从输入数据中读入前 k 个记录构建初始缓冲区。
构造败者树，用于维护缓冲区中记录的最小值。

2. 输出最小值并更新

每次通过败者树找到当前缓冲区中的最小记录（根节点）。
将最小记录输出到外存，填充新数据到被替换的位置。
如果新数据的值小于当前输出记录，则将其标记为“不可参与本段”（设置为“哨兵值”），直到开启新段。

3. 新段生成

当缓冲区中的所有值都比输出的最小值小（即标记为“哨兵值”），当前归并段结束，记录段的边界。
继续处理剩余数据，重复以上过程，直到所有输入数据被处理完。

4. 输出初始归并段

最终生成多个初始归并段，每段可以直接用于外部排序的归并阶段。

最佳归并树

k路最佳归并树是为了解决k路归并排序中最小化比较次数的问题，它是最佳归并树的扩展版本，但区别在于一次可以归并k个序列，而不仅仅是两两归并。

构造思想

设初始归并段为m个，进行k-路归并

若 $(m-1) \mod (k-1) \neq 0$ : 则需附加 $(k-1)-(m-1) \mod (k-1)$ 个长度为0的虚段
按照哈夫曼树的构造原则（权值越小的结点离根结点越远）构造最佳归并树，权值为归并段长度。

k路最佳归并树的示例

示例：

有6个序列，长度分别为：10, 20, 30, 40, 50, 60，我们希望使用 3路归并 来最小化比较代价。

构造过程：

给定数据

初始序列长度为: 10, 20, 30, 40, 50, 60 (6个序列, $m = 6$ )

使用3路归并 ( $k = 3$ ):

第一步: 检查是否需要补充虚段

计算 $(m - 1) \mod (k - 1)$ :

$(6 - 1) \mod (3 - 1) = 5 \mod 2 = 1$

因为结果不为0, 需要补充:

$(k - 1) - (m - 1) \mod (k - 1) = 2 - 1 = 1$

补充一个长度为0的虚段。新的序列为: 10, 20, 30, 40, 50, 60, 0.

第二步: 按哈夫曼树规则进行归并

第一轮合并

选择最小的三个序列 0, 10, 20, 合并后的长度为:

$0 + 10 + 20 = 30$

剩余序列为: 30, 30, 40, 50, 60

第二轮合并

选择最小的三个序列 30, 30, 40, 合并后的长度为:

$30 + 30 + 40 = 100$

剩余序列为: 50, 60, 100

第三轮合并

选择最小的三个序列 50, 60, 100, 合并后的长度为:

$50 + 60 + 100 = 210$

剩余序列为: 210

k路最佳归并树的图示


               (210)

              /  |  \

           (100) 60  50

          / | \ 

      (30) 30  40

     / | \

   10 20 0

与其他树的区别

特性	最佳归并树	胜者树	败者树
用途	最小化归并代价	快速找到多路最优元素	快速找到多路最优元素
构造过程	基于哈夫曼树思想	二叉树逐层比较	二叉树逐层比较
代价最小化	最小化归并比较总次数	不关注总次数，仅找最优值	不关注总次数，仅找最优值
适用场景	多路归并排序、文件合并	归并排序、优先级队列	归并排序、优先级队列

外部排序_