栈、队列是一种特殊（操作受限）的线性表。区别：仅在于运算规则不同

栈

栈是一种数据结构，它遵循“后进先出”（LIFO, Last In First Out）的原则。

定义：只能在表的一端（栈顶）进行插入和删除运算的线性表

逻辑结构：与线性表相同，仍为一对一关系

存储结构：用顺序栈或链栈存储均可，但以顺序栈更常见

运算规则：只能在栈顶运算，且访问结点时依照后进先出（LIFO）或先进后出（FILO）的原则

基本操作：基本操作有入栈、出栈、读栈顶元素值、建栈、判断栈满、栈空等

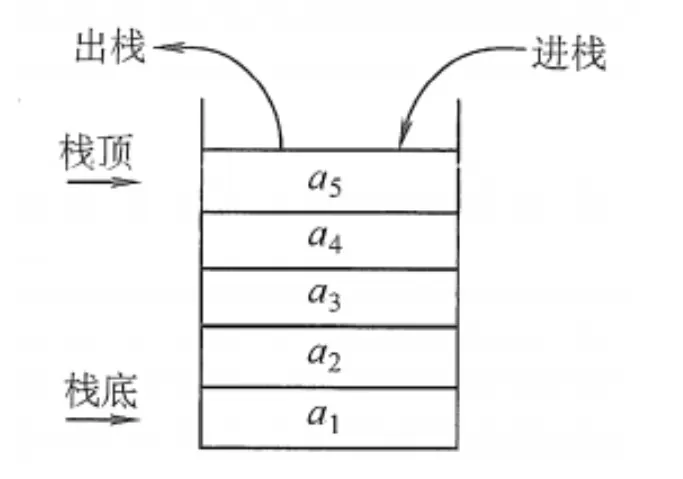
1729304664675

栈顶（Top）：线性表允许进行插入删除的那一端。栈底（Bottom）：固定的，不允许进行插入和删除的另一端。空栈：不含任何元素的空表。

顺序栈

采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针（top）指示当前栈顶元素的位置。

若存储栈的长度为StackSize，则栈顶位置top必须小于StackSize。当栈存在一个元素时，top等于0，因此通常把空栈的判断条件定位top等于-1。

顺序栈可以如此定义：

#define MAXSIZE 50  //定义栈中元素的最大个数
typedef int ElemType;   //ElemType的类型根据实际情况而定，这里假定为int
typedef struct{
    ElemType data[MAXSIZE];
    int top;    //用于栈顶指针
}SqStack;

顺序栈的基本用法

初始化

void InitStack(SqStack *S){
    S->top = -1;    //初始化栈顶指针
}

判断空栈

bool StackEmpty(SqStack S){
    if(S.top == -1){  
        return true;    //栈空
    }else{  
        return false;   //不空
    }
}

进栈

bool  Push(SqStack *S, ElemType e){
    //满栈
    if(S->top == MAXSIZE-1){
        return false;
    }
    S->top++;   //栈顶指针增加一
    S->data[S->top] = e;    //将新插入元素赋值给栈顶空间
    return true;
}

出栈

bool Pop(SqStack *S, ElemType *e){
    if(S->top == -1){
        return true;
    }
    *e = S->data[S->top];   //将要删除的栈顶元素赋值给e
    S->top--;   //栈顶指针减一
    return false;
}

获取栈顶元素

bool GetTop(SqStack S, ElemType *e){
    if(S->top == -1){   //栈空
        return false;
    }
    *e = S->data[S->top];   //记录栈顶元素
    return true;
}

链栈

采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。通常采用单链表实现，并规定所有操作都是在单链表的表头进行的。这里规定链栈没有头节点，Lhead指向栈顶元素，如下图所示。

1729304698420

链栈的代码定义如下：

/*栈的链式存储结构*/
/*构造节点*/
typedef struct StackNode{
    ElemType data;
    struct StackNode *next;
}StackNode, *LinkStackPrt;
/*构造链栈*/
typedef struct LinkStack{
    LinkStackPrt top;
    int count;
}LinkStack;

这里的 *LinkStackPrt 是对 struct StackNode的重命名，LinkStackPrt top; = struct StackNode * top

进栈

bool Push(LinkStack *S, ElemType e){
    LinkStackPrt p = (LinkStackPrt)malloc(sizeof(StackNode));
    p->data = e;
    p->next = S->top;    //把当前的栈顶元素赋值给新节点的直接后继
    S->top = p; //将新的结点S赋值给栈顶指针
    S->count++;
    return true;
}

出栈

bool Pop(LinkStack *S, ElemType *e){
    LinkStackPtr p;
    if(StackEmpty(*S)){
        return false;
    }
    *e = S->top->data;
    p = S->top; //将栈顶结点赋值给p
    S->top = S->top->next;  //使得栈顶指针下移一位，指向后一结点
    free(p);    //释放结点p
    S->count--;
    return OK;
}

栈模板c++

这里我写好了一个通过模板实现的栈，只有几个基础的功能，以后可以直接放在头文件中使用：“stack.h”

#ifndef STACK_H
#define STACK_H

#include <iostream>

template <typename T>
struct StackNode {
    T data;
    StackNode<T> *next;
};

template <typename T>
using LinkStackPtr = StackNode<T>*;

template <typename T>
class Stack {
private:
    LinkStackPtr<T> top;
    int count;
public:
    Stack() : top(nullptr), count(0) {} // 构造函数初始化
    ~Stack(); // 析构函数
    bool Push(T v);
    bool Pop(T* v);
    bool IsEmpty();
    bool GetTop(T* v);
};

template <typename T>
Stack<T>::~Stack() {
    T value;
    while (this->Pop(&value)) {
        // 释放所有节点
    }
}


template <typename T>
bool Stack<T>::Push(T v)
{
    StackNode<T>* tmp = new StackNode<T>;
    if (!tmp)
        return false;
    tmp->data = v;
    tmp->next = this->top;
    this->top = tmp;
    (this->count)++;
    return true;
}
template <typename T>
bool Stack<T>::Pop(T* v)
{
    if(this->IsEmpty())
        return false;
    LinkStackPtr<T> tmp = this->top;
    *v = tmp->data;
    this->top = this->top->next;
    delete tmp;
    (this->count)--;
    return true;
}

template <typename T>
bool Stack<T>::IsEmpty()
{
    return this->top == nullptr;
}

template <typename T>
bool Stack<T>::GetTop(T* v) 
{
    if(this->IsEmpty())
        return false;
    *v = this->top->data;
    return true;
}

#endif // STACK_H

递归

递归是栈的一种重要的应用

递归条件

递归表达式（递归体）
边界条件（递归出口）

队列

定义：只能在表的一端（队尾）进行插入，在另一端（队头）进行删除运算的线性表

逻辑结构：与线性表相同，仍为一对一关系

存储结构：用顺序队列或链队存储均可

运算规则：先进先出（FIFO）

实现方式：关键是编写入队和出队函数，具体实现依顺序队或链队的不同而不同

顺序队列

队列的顺序实现是指分配一块连续的存储单元存放队列中的元素，并附设两个指针：队头指针 front指向队头元素，队尾指针 rear 指向队尾元素的下一个位置。

顺序队列的代码定义

#define MAXSIZE 50	//定义队列中元素的最大个数
typedef struct{
	ElemType data[MAXSIZE];	//存放队列元素
	int front,rear;
}SqQueue;

初始状态（队空条件）：Q->front == Q->rear == 0。进队操作：队不满时，先送值到队尾元素，再将队尾指针加1。出队操作：队不空时，先取队头元素值，再将队头指针加1。

根据以上的规则我们不难发现，不论是front还是rear都会不断地怎加，最后一一定会跑出我们规定的范围，为了解决这一问题，我们通过循环队列来是实现：

循环队列

解决假溢出的方法就是后面满了，就再从头开始，也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。

当队首指针 Q->front = MAXSIZE-1后，再前进一个位置就自动到0，这可以利用除法取余运算（%）来实现。

初始时 ：Q->front = Q->rear=0
队首指针进1 ：Q->front = (Q->front + 1) % MAXSIZE
队尾指针进1 ：Q->rear = (Q->rear + 1) % MAXSIZE
队列长度 ：(Q->rear - Q->front + MAXSIZE) % MAXSIZE

无论出队还是入队，front和rear都向前+1。

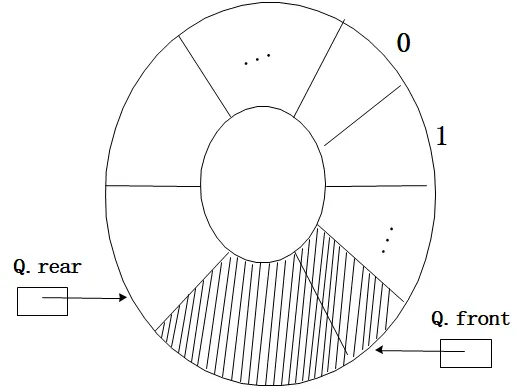
1729301790512

此处我们为了避免判空和判满的条件一样，牺牲一个位置不存放信息
- 队列判空的条件为：Q->front == Q->rear
- 队满的判断条件为：(Q->rear+1)%Maxsize == Q->front
- 队列中的元素个数：(Q->rear - Q->front + MAxsize)%Maxsize
类型中增设表示元素个数的数据成员。这样，队空的条件为 Q->size == O ；队满的条件为 Q->size == Maxsize 。这两种情况都有 Q->front == Q->rear
类型中增设tag 数据成员，以区分是队满还是队空。tag 等于0时，若因删除导致 Q->front == Q->rear ，则为队空；tag 等于 1 时，若因插入导致 Q ->front == Q->rear ，则为队满。

循环队列的代码实现

定义

typedef int ElemType;   //ElemType的类型根据实际情况而定，这里假定为int
#define MAXSIZE 50  //定义元素的最大个数
/*循环队列的顺序存储结构*/
typedef struct{
    ElemType data[MAXSIZE];
    int front;  //头指针
    int rear;   //尾指针,若队列不空，指向队列尾元素的下一个位置
}SqQueue;

初始化

bool InitQueue(SqQueue *Q){
    Q->front = 0;
    Q->rear = 0;
    return true;
}

判空

/*判队空*/
bool isEmpty(SqQueue Q){
    if(Q.rear == Q.front){
        return true;
    }else{
        return false;
    }
}

求队列长度

int QueueLength(SqQueue Q){
    return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}

入队

bool EnQueue(SqQueue *Q, ElemType e){
    if((Q->rear + 1) % MAXSIZE == Q->front){
        return false;   //队满
    }
    Q->data[Q->rear] = e;   //将元素e赋值给队尾
    Q->rear = (Q->rear + 1) % MAXSIZE;  //rear指针向后移一位置，若到最后则转到数组头部
    return true;
}

出队

bool DeQueue(SqQueue *Q, ElemType *e){
    if(isEmpty(Q)){
        return false;   //队列空的判断
    }
    *e = Q->data[Q->front]; //将队头元素赋值给e
    Q->front = (Q->front + 1) % MAXSIZE;    //front指针向后移一位置，若到最后则转到数组头部
    return true;
}

链队列

队列的链式存储结构表示为链队列，它实际上是一个同时带有队头指针和队尾指针的单链表，只不过它只能尾进头出而已 。

在这里插入图片描述

空队列时，front和real都指向头结点。

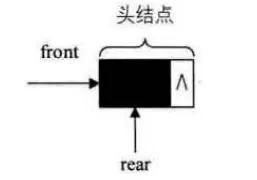
1729303485984

代码定义

/*链式队列结点*/
typedef struct {
	ElemType data;
	struct LinkNode *next;
}LinkNode;
/*链式队列*/
typedef struct{
	LinkNode *front, *rear;	//队列的队头和队尾指针
}LinkQueue;

初始化

void InitQueue(LinkQueue *Q){
	Q->front = Q->rear = (LinkNode)malloc(sizeof(LinkNode));	//建立头结点
	Q->front->next = NULL;	//初始为空
}

入队

bool EnQueue(LinkQueue *Q, ElemType e){
	LinkNode s = (LinkNode)malloc(sizeof(LinkNode));
	s->data = e;
	s->next = NULL;
	Q->rear->next = s;	//把拥有元素e新结点s赋值给原队尾结点的后继
	Q->rear = s;	//把当前的s设置为新的队尾结点
	return true;
}

出队

bool DeQueue(LinkQueue *Q, Elemtype *e){
	LinkNode p;
	if(Q->front == Q->rear){
		return ERROR;
	}
	p = Q->front->next;	//将欲删除的队头结点暂存给p
	*e = p->data;	//将欲删除的队头结点的值赋值给e
	Q->front->next = p->next;	//将原队头结点的后继赋值给头结点后继
	//若删除的队头是队尾，则删除后将rear指向头结点
	if(Q->rear == p){
		Q->rear = Q->front;
	}
	free(p);
	return OK;
}

栈和队列_

栈

顺序栈