c++

注意所有的数据结构都在std命名空间下使用。注意在代码开头加入：

using namespace std;

为节省时间可以：

typedef long long ll;

如果long long 也无法满足你，请依次尝试：

• unsigned long long
• __int128
• unsigned __int128

CCF真的很狗，如果你不确定会不会超过long long，请直接使用 unsigned __int128

数据类型转换：有符号数与size_t做比较，一定要先将size_t转为有符号数，否则最终结果为无符号数，一定>=0。

i - (int)word.length() >= 0

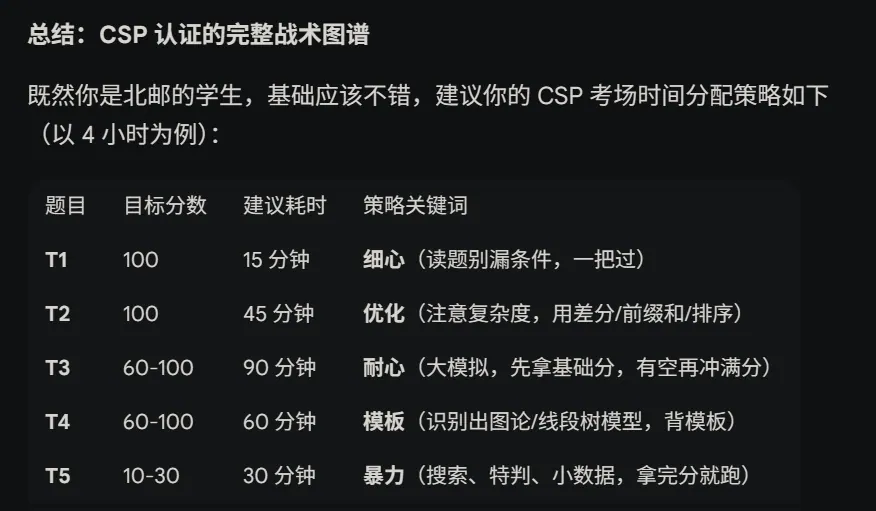
IO简要熟悉

IO优化

C++默认输入输出(cin/cout)为了兼容C语言的输入输出，做了一些额外的工作，导致它们比C语言慢很多。

基础IO优化就是关掉这些额外工作，导致让 cin和 cout跑的飞快，甚至比 scanf还快。

ios::sync_with_stdio(false);
cin.tie(nullptr);

1. ios::sync_with_stdio(false):
   • 取消C++标准流与C标准流的同步
   • 副作用：不能再使用 sanf、printf、getchar等c语言风格的代码
2. cin.tie(nullptr)：
   • 解除 cin和 cout的绑定
   • 作用：执行 cin之前，不会再检查输出缓冲区中的是否有东西。

尽量别使用 endl：

• cout << endl; 等价于 cout << "\n" << flush;
• 不仅会换行，还会强制刷新缓冲区。
• 优化方法：在输出大量数据(比如输出N个换行)时，请使用 "\n"代替 endl

cout << ans << endl; //慢，频繁刷新硬盘/屏幕
cout << and << "\n"; //快，先攒在内存里，攒够了一起发

在acwing中某一题中，开启io优化前后效果如下：

上方的提交无IO优化

下方的提交开启了IO优化

时间缩短了 1/3。

格式化输出

如果你关闭了同步流，对于程序的输出，建议只使用 cout或 printf()中的一种。

1. 保留N位小数

   printf("%.2lf\n",x);	//输出3.14，保留两位小数

2. 补0

   printf("%03d\n", t); 	//输出005，凑齐三位

字符串与整行读取(T3 大模拟)

cin >> s遇到空格就会停止。如果题目说”输入一行包含空格的指令”，必须用 getline.

string s;
getline(cin, s); // 读取整行，包括空格

注意事项

如果你先读取了一个数字，紧接着要读取一行字符串，必须手动处理前一行遗留的回车符。

int n;
cin >> n;
cin.ignore(); // ✅ 忽略掉缓冲区里的一个字符（即换行符）
// 或者用 getline(cin, s) 读到一个废弃变量里也可以
string s;
getline(cin, s); // 现在读到的才是真正的下一行

stringstream 空格切割机

使用 getline()读取一行的数据后，我们往往还需要解析其中的内容。

#include <sstream>

stringstream ss(line); // 初始化流

string word;
while(ss >> word){
    //ss会自动跳过空格，将单词提取出来
}

字符串$\leftrightarrow$数字转换

字符串转数字：#include <string>

• stoi()：string To int
• stoll()：string To long long
• stof()：string To float
• stod()：string To double

数字转字符串：

int x = 123;
string s = to_string(x); // 结果 "123"

格式化读取

在处理固定格式的字符串时，C语言的 sscanf()比正则表达式还好用。

场景：题目输入日期格式 2025-11-21 或 IP 地址 192.168.1.1。

#include <cstdio> // 必须包含

char date[] = "2025-11-21";
int year, month, day;

// %d 读整数，- 是分隔符
sscanf(date, "%d-%d-%d", &year, &month, &day); 

// 此时 year=2025, month=11, day=21
// 这比用 find 和 substr 切割字符串快10倍

实际使用时，先使用 cin或 getline等方法读取字符串，再使用 sscanf()解析数据

容器(vector)

C++中的 vector等于Java中的 ArrayList。

头文件：#include <vector>

创建空int类型示例：

vector<int> myVector;

快速初始化：

vector<int> myVector(5) // 创建一个包含 5 个整数的 vector，每个值都为默认值（0）
vector<int> myVector(5, 10); // 创建一个包含 5 个整数的 vector，每个值都为 10
vector<int> vec2 = {1, 2, 3, 4}; // 初始化一个包含元素的 vector

常用方法

获取大小

size_t size = myVector.size();

获取最后一个元素

int last = myVcter.back();

插入

1. 末尾插入：

   myVector.push_back(7); //将7添加到末尾

2. 中间插入：

   myVector.insert(myVector.begin(), 5); //将5添加到下标为0位置
   myVector.insert(myVector.begin()+2,10);//将10添加到下标为2的位置

访问

随机访问：

int x = myVector[0];	//直接访问，越界直接崩溃
int y = myVector.at(1); //方法访问，稍慢，但越界时会抛出异常

遍历访问：

//下标访问
vector<int> v = {1, 2, 3, 4, 5};
for (size_t i = 0; i < myVector.size(); ++i) {
    cout << v[i] << " ";
}

//增强for循环,不能修改元素
for (int x : myVector) {
    cout << x << " ";
}

//使用引用，可以修改元素
for (int &x : myVector) {
    x *= 2;  // 每个元素翻倍
}

//迭代器
for (auto it = myVector.begin(); it != myVector.end(); ++it) {
    cout << *it << " ";
}

删除元素

1. 删除末尾元素：

   myVector.pop_back();

2. 删除指定下标元素：

   myVector.erase(myVector.begin()+2); 	//删除下标为2的元素

3. 删除连续多个元素：

   myVector.(myVector.begin()+1, myVector.begin()+4); //删除下标[1,4)的元素

4. 清空所有元素：

   myvector.clear();

排序Sort

头文件：#include <algorithm>

默认升序排序：

sort(myVector.begin(), myVector.end());

自定义排序规则：

//定义cmp函数
bool cmp(int a , int b){
    return a > b;	//降序排列
}

sort(myVector.begin(), myVector.end(), cmp);
//一种简写:
sort(myVector.begin(), myVector.end(), greater<int>()); //使用默认比较器

a > b 为为降序排列，a < b为升序排列。

• greater<>：降序
• less<>：升序

记忆技巧：

当我们参数申明顺序为 bool cmp(int a , int b)时，在返回比较结果前，我们依然将a写在前，b写在后如 a b。

我们将a、b当作排序后列表中的相邻元素，顺序同样为a在前，b在后。

如果为升序即为前面的元素a小，后面的元素b大，则 a < b

如果降序则前面的元素a大，后面的元素b小，则 a > b

引用

C++中的引用与Java中的引用概念相似，是一种为已有变量起别名的机制。

为什么在这里突然讲解引用呢？因为在给sort函数传递自定义 cmp函数时，我们一定要注意什么时候我们必须传递引用。这会极大的影响程序的运行时间。我们结合一道leetcode中的题目为例：

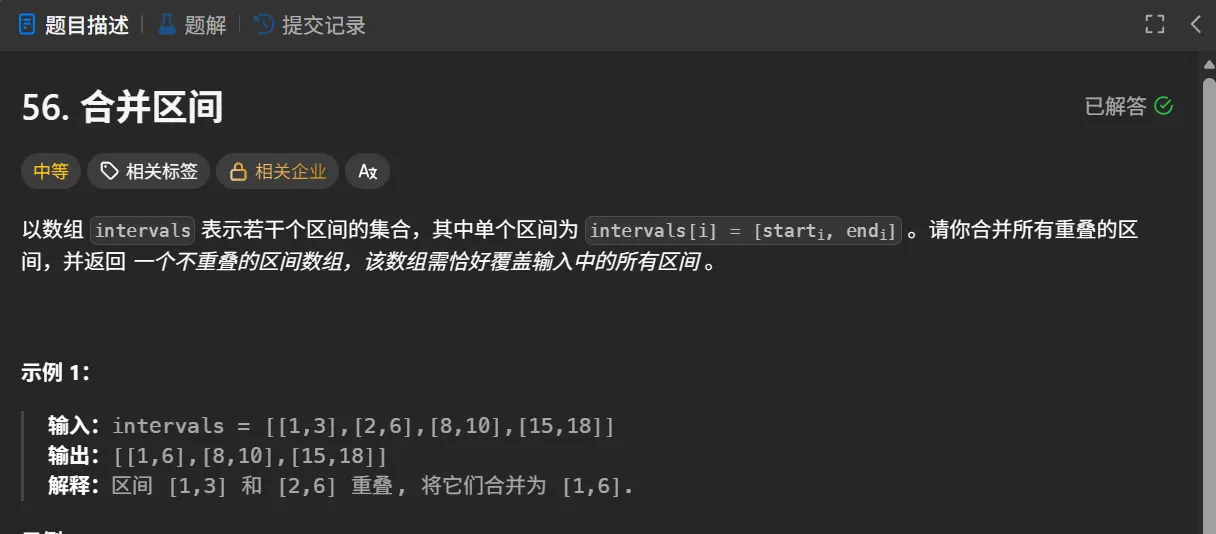
这道题的常见思路如下：

using namespace std;

bool cmp(vector<int> a, vector<int> b){
    return a[0] < b[0];
}

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp);
        vector<vector<int>> res;
        int i = 0;
        while(i < intervals.size()){
            int j = 1;
            while(i+j < intervals.size() && intervals[i][1] >= intervals[i+j][0]){
                intervals[i][1] = max(intervals[i][1], intervals[i+j][1]);
                j++;
            }
            res.push_back(intervals[i]);
            i = i+j;
        }
        return res;
    }
};

由于我们比较的是 vector<int>类型，所以我传入 cmp方法，定义按照数组的首元素降序排序。

此时它的运行时间如下：

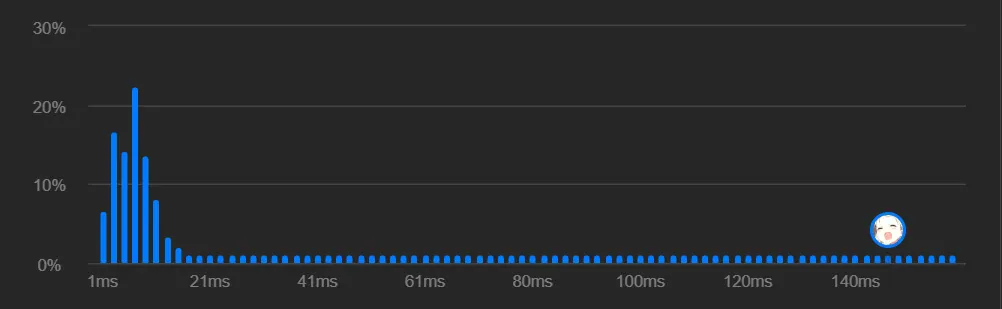
为什么这么慢呢？就是因为 cmp方法中我没有传 vector<>的引用，而是直接传了形参。此时c++在传递参数时会将原本的 vector<int>完整的拷贝一遍，这不仅浪费大量的空间，还浪费大量的时间。

我们仅需将cmp做小小改动如下：

bool cmp(vector<int> &a, vector<int> &b){
    return a[0] < b[0];
}

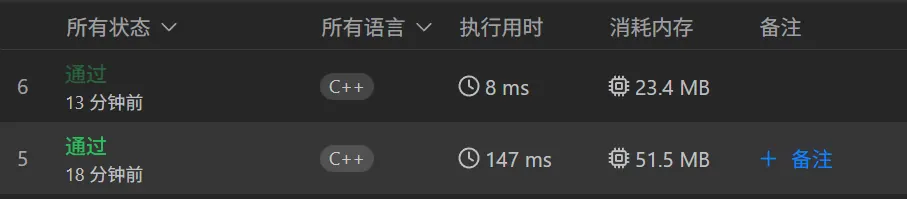
不管是时间还是空间都可以得到大幅优化。

Map

在c++中，常用的map有4种，分别是 std::map、std::multimap、std::unordered_map、std::unordered_multimap。

容器类型	底层结构	是否有序	键是否唯一	查找时间复杂度	头文件
std::map	红黑树	有序	唯一	O(log n)	<map>
std::multimap	红黑树	有序	可重复	O(log n)	<map>
std::unordered_map	哈希表	无序	唯一	O(log n)	<unordered_map>
std::unordered_multimap	哈希表	无序	可重复	O(log n)	<unordered_map>

通用属性：

• map.size()
• map.empty()
• map.begin()

创建map

四种哈希表的默认构造都一样，只需声明键和值的数据类型即可：

std::map<int, std::string> m;

有序Map

基于红黑树实现的 map和 multimap可以指定比较器：

std::map<int, std::string, std::greater<int>> m; // 降序
std::multimap<int, std::string, std::less<int>> mm; // 升序，与默认相同

自定义比较器：

struct MyCompare{
    bool operator()(int a , int b) const {
        return a > b;   
    }
};  //等效 greater<int>

哈希Map

基于哈希表实现的 ordered_map和 ordered_multimap，可以指定哈希函数和相等比较器：

struct MyHash{
    size_t operator()(int& key) const{    //参数为自定义结构体时一定要传引用
        return hash<int>()(key);	//注意有两对括号
    }
};

struct MyEqual{
    bool operator()(int& a, int &b) const{
        return a == b;
    }
};

unordered_map<int, std::string, MyHash, MyEqual> um;

与java中相同，如果map中存储的为自定义类型，一定要同时重写 MaHash和 MyEqual方法。

插入元素

四种map的插入元素均可使用：

m.insert({key, value});

针对 map和 unorder_map唯一键的map，可以使用操作符 []。

m[key] = value;	//如果不存在为插入，如果存在为修改
m.at(key) = value; //支持使用at

查找元素

1. find(key)
   • 返回指向第一个匹配元素的迭代器
   • 如果没找到返回end()
2. count(key)
   • 返回匹配该键的元素的数量
   • 唯一键map返回0/1
   • 重复键返回值可能大于1
3. equal_range(key)
   • 返回一对迭代器，表示所有匹配该键的范围。

修改元素

唯一键map

• 支持操作符 []：

m[key] = value;	//如果不存在为插入，如果存在为修改
m.at(key) = value; //支持使用at

• 使用迭代器：

auto it = m.find(key);
if(it !- m.end()) {
    it->second = newValue;
}

重复键map

只能通过迭代器修改：

auto range = mm.equal_range(key);
for(auto it = range.first; it != range.second; ++it) {
    if(/*条件*/) {
	it->second = newValue;
    }
}

• mm.equal_range()：返回一对迭代器，表示所有匹配该键的范围。
  • range.first指向匹配的第一个元素位置
  • range.second指向最后一个匹配元素的下一个位置

如果在重复键map中使用 .find()，会返回第一个匹配的元素。

删除元素

1. 按键删除：

m.erase(key);

• 唯一键map：删除该键唯一定义元素。
• 重复键map：删除该键对应的所有元素。

2. 按迭代器删除：

auto it = m.find(key);

if(it != m.end())){
    m.erase(it);
}

3. 清空容器

m.clear();

Pair

头文件：#include <utility>

用来存储两个数据成员，可以是不同类型的两个值。

创建pair

pair<int, string> p1(1, "one");       // 构造函数
auto p2 = make_pair(2, "two");   // make_pair 辅助函数
pair<int, string> p3 = {3, "three"};  // 列表初始化

访问元素

• first：第一个值
• second：第二个值

cout << p1.first;   // 1
cout << p1.second;  // "one"

修改元素

p1.first = 10;
p1.second = "ten";

比较操作

pair支持比较运算符(==，<，>等)

比较规则：先比较 first，如果相等再比较 second

pair<int, int> a(1, 2), b(1, 3);
cout << (a < b);  // true，因为 2 < 3

Set

set的实现与Map类似，常用的有四种：set、multiset、unordered_set、unordered_multiset。

容器类型	底层结构	是否有序	键是否唯一	查找时间	时间复杂度	头文件
set	红黑树	✅ 有序	✅ 唯一	O(log n)	插入/删除/查找 O(log n)	<set>
multiset	红黑树	✅ 有序	❌ 可重复	O(log n)	插入/删除/查找 O(log n)	<set>
unordered_set	哈希表	❌ 无序	✅ 唯一	平均 O(1)，最坏 O(n)	插入/删除/查找 平均 O(1)	<unordered_set>
unordered_multiset	哈希表	❌ 无序	❌ 可重复	平均 O(1)，最坏 O(n)	插入/删除/查找 平均 O(1)	<unordered_set>

通用属性：

• size()
• empty()

创建Set

set的创建与map相似，只不过只需要传入一个数据类型即可：

set<int> s;

有序set可以传入比较器：

struct MyCompare{
    bool operator()(int a , int b) const {
        return a > b;   
    }
};  //等效 greater<int>

set<int, greater<int>> s;	//降序排列
multiset<int, MyCompare> ms;	//使用自定义排序器

哈希表set可以传入哈希函数和相等比较函数。

struct MyHash{		//针对key
    size_t operator()(int& key) const{    //参数为自定义结构体时一定要传引用
        return hash<int>()(key);	//注意有两对括号
    }
};

struct MyEqual{		//针对value
    bool operator()(int& a, int &b) const{
        return a == b;
    }
};

unordered_set<int, MyHash, MyEqual> um;

插入元素

四种set都使用 insert()方法进行插入，只是唯一元素set和重复元素set的insert()方法返回值略有不同。

唯一元素set：

• 返回：pair<iterator, bool>
  • iterator：指向元素的位置
  • bool：表示是否插入成功

set、map等排序元素，迭代器不能加减运算，但可以自增。

set<int> s;
auto [it, ok] = s.insert(10); // ok=true
auto [it2, ok2] = s.insert(10); // ok2=false

可重复元素set：

• 返回：iterator：指向新插入的元素。

std::multiset<int> ms;
auto it = ms.insert(10); // 插入成功
auto it2 = ms.insert(10); // 也成功，允许重复

批量插入：insert(first, last);

接收两个迭代器first和last表示插入的范围 [first, last)，这两个迭代器可以来自任何符合标准的容器（如 std::vector、std::list 等）,此时它没有返回值。

该方法批量插入其他容器的值。

set<int> s;
vector<int> v = {1, 2, 3};
s.insert(v.begin(), v.end());

查找元素

所有的set都支持以下四种查找方法：

• find(key)：返回迭代器。
• count(key)：返回匹配元素个数。
  • set中只能是0/1
  • multiset中可能大于1
• equal_range(key)：返回一对迭代器，表示所有匹配元素的范围。

set<int> s = {1, 2, 3};
auto it = s.find(2); // 指向元素 2
if (it != s.end()) { /* 找到 */ }

multiset<int> ms = {1, 2, 2, 3};
size_t cnt = ms.count(2); // cnt = 2
auto range = ms.equal_range(2); // 范围包含两个 2

删除元素

所有的set都支持使用erase()方法来删除元素：

• erase(iterator pos)：删除迭代器指向的元素。
• erase(key)：删除值为 key 的元素
  • set：删除一个元素
  • multiset：删除所有相等元素
  • 返回成功删除元素的个数
• erase(iterator first, iterator last)：批量删除。
  • 对于无序set可能意义不大。
  • 对于有序set可以删除一个大小区间内的所有值
• clear()：删除所有元素。

std::set<int> s = {1, 2, 3};
s.erase(2); // 删除元素 2，返回 1
s.erase(s.begin()); // 删除第一个元素
s.clear(); // 清空集合

std::multiset<int> ms = {1, 2, 2, 3};
size_t n = ms.erase(2); // 删除所有 2，返回 2

批量删除与批量插入不同，批量删除时的首尾迭代器都只能来自 set自己。

set<int> s = {1, 2, 3, 4, 5};
s.erase(s.begin(), s.find(4));  // 删除 1, 2, 3

set运算

set运算的函数在头文件 #include <algorithm>中，不仅可以对 set类型使用，对于 vector<>等页可以使用。

set运算对于unordered_set不可用。

取交集

取交集使用函数：set_intersection()

int main(){
    vector<int> v = {1,2};
    set<int> s = {2, 3, 4};
    vector<int>res;
    set_intersection(s.begin(),s.end(), v.begin(), v.end(), back_inserter(res));
    for(int n : res)
        cout << n;
}

取并集

取并集使用函数：set_union()

int main(){
    vector<int> v = {1,2};
    set<int> s = {3, 4};
    vector<int>res;
    set_union(s.begin(),s.end(), v.begin(), v.end(), back_inserter(res));
    for(int n : res)
        cout << n;
}

Deque

Stack

Stack 是容器适配器，底层基于 deque

容器适配器：不是新的容器，而是对已有容器的封装，提供更简化、更特定的接口。

头文件：#include <stack>

栈的使用非常简单，只有几种常见的简单操作：

1. 创建栈：

stack<int> s;   // 定义一个存储 int 类型的栈
stack<string> st; // 定义一个存储 string 类型的栈

2. 常用操作
   • s.push(x)：将元素压入栈顶
   • s.pop()：弹出栈顶元素（不返回值）
   • s.top()：访问栈顶元素
   • s.empty()：判断栈是否为空
   • s.size()：返回栈中元素数量

Queue

Queue也是适配性容器。底层是 deque

头文件：#include <queue>

1. 创建队列：

queue<int> q;   // 定义一个存储 int 的队列
queue<string> qs; // 定义一个存储 string 的队列

2. 常用操作
   • q.push(x)：在队尾插入元素
   • q.pop()：删除队头元素（不返回值）
   • q.front()：访问队头元素
   • q.back()：访问队尾元素
   • q.empty()：判断队列是否为空
   • q.size()：返回队列中元素数量

Deque

双端队列。

头文件：#include <deque>

操作	功能说明
push_back()	在尾部插入元素
push_front()	在头部插入元素
pop_back()	删除尾部元素
pop_front()	删除头部元素
at(pos)	返回指定位置元素（带范围检查）
operator[]	返回指定位置元素（不检查范围）
front()	获取第一个元素
back()	获取最后一个元素
begin()/end()	获取迭代器（正向遍历）
size()	返回元素个数
empty()	判断容器是否为空
clear()	清空所有元素
insert()	在指定位置插入元素
erase()	删除指定位置或区间元素

String

截取、查找、拼接

截取子串 substr()

语法：

• s.substr(pos, len)：指定开始位置与截取的长度
• s.substr(pos)：未指定长度，将截取从 pos开始的所有字符

string s = "2025-11-22";
string year = s.substr(0, 4);  // "2025" (从下标0开始，取4个)
string month = s.substr(5, 2); // "11"
string tail = s.substr(5);     // "11-22" (从5开始一直到结束)

查找位置 find()

查找某个字符或字串第一次出现的位置。

• 语法：
  • find(target)：查找第一次出现的位置。
  • find(target, pos)：从pos下标开始找。
• 返回值：返回下标(size_t类型)
• 判空：如果找不到，返回 string::npos(这是一个常数)

string s = "[email protected]";
size_t pos = s.find('@');

if (pos != string::npos) {
    cout << "找到 @ 在下标: " << pos << endl;
} else {
    cout << "非法邮箱" << endl;
}

拼接 +和 +=

将多个字符串连接起来。

注意：尽量用 +=，效率略高于 s = s +

string s = "Hello";
s += " World"; // s 变为 "Hello World"
s += '!';      // 也可以追加单个字符

修改操作：删、插、换

删除 erase

• 语法：s.erase(pos, len)
• 作用：从 pos开始删除 len个字符

string s = "Hello World";
s.erase(5, 1); // 删除下标5开始的1个字符（即空格）
// s 变为 "HelloWorld"

插入 insert

• 语法：s.insert(pos, str)
• 用途：在 pos下标之前插入字符串

string s = "HeWorld";
s.insert(2, "llo "); 
// s 变为 "Hello World"

替换 replace

• 语法：s.replace(pos, len, new_str)
• 用途：将从 pos开始的 len个字符替换为 new_str

string s = "I love Java";
s.replace(7, 4, "C++"); // 把 "Java" (4个字符) 换成 "C++"
// s 变为 "I love C++"

类型转换

• 数字转字符串：to_string(val)

  int a = 123;
  string s = to_string(a);

• 字符串转数字：

  • stoi(s)：int
  • stoll(s)：转 long long (CSP建议用这个，防止溢出)
  • stod(s)：转 double

常用算法

快速幂算法

将计算$a^b$的时间复杂度从O(b)降低到O(logb)

核心思想：二进制拆分

我们计算$3^{11}$。普通算术是：$3 \times 3 \times 3 \dots$ 乘 11 次。

快速幂的思想是利用二进制：

1. 把指数11写成二进制：(1011)。
2. 这意味着：$11 = 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 8 + 2 + 1$。
3. 所以：

$$3^{11} = 3^{(8 + 2 + 1)} = 3^8 \times 3^2 \times 3^1$$

我们只需要知道$3^1, 3^2, 3^4, 3^8 \dots$这些权重为2的幂次的值，然后把二进制位为1的那些项乘起来即可。

代码实现

通常题目会要求对结果取模：

#include <iostream>

using namespace std;

typedef long long ll;

// 计算 (a ^ b) % m
ll qpow(ll a, ll b, ll m) {
    ll res = 1;      // 存储结果
    a %= m;          // 预处理：如果底数本身就比 m 大，先取模
  
    while (b > 0) {
        // 1. 判断 b 的最后一位是否为 1 (等价于 b % 2 == 1)
        if (b & 1) {
            res = (res * a) % m; // 如果是 1，就把当前的权重乘到结果里
        }
  
        // 2. 底数自乘 (翻倍权重: a^1 -> a^2 -> a^4 -> a^8 ...)
        a = (a * a) % m;
  
        // 3. 指数右移一位 (除以 2: 11 -> 5 -> 2 -> 1)
        b >>= 1;
    }
    return res;
}

int main() {
    // 计算 2 的 100 次方 对 10^9 + 7 取模
    ll base = 2;
    ll exponent = 100;
    ll mod = 1e9 + 7;
  
    cout << qpow(base, exponent, mod) << endl;
    return 0;
}

倍增法

倍增法的核心思想与快速幂相似：不要一步一步走，而是按2的幂次跳着走。

任何整数k都可以被分解为2的幂次之和(二进制表示)。例如：如果要走13步，二进制为(1101)8 + 4 + 1，我们只预先需要计算：

• 走$2^0 = 1$步到了哪。
• 走$2^1 = 2$步到了哪。
• 走$2^2 = 4$步到了哪。
• …
• 走$2^{30}$步到了哪。

然后组合这些跳板即瞬间可到达目的地。把O(k)的线性操作降维成O(log k)的操作。

预处理：造表

假设 dp[u][i]的物理意义是：从状态u出发，经过$2^i$步，到达的状态。

我们要从小到达填满这个 dp表。

• dp[u[0]：走$2^0=1$步。这是题目直接告诉你的（比如 a -> b）。
• dp[u][1]：走 $2^1=2$ 步。等于先走 1 步，再走 1 步。
• dp[u][i]：走 $2^i$ 步。等于先走 $2^{i-1}$ 步（一半），再从那里走 $2^{i-1}$ 步（另一半）。

状态转移的核心公式：

$$dp[u][i] = dp[\; dp[u][i-1] \;][i-1]$$

查询：拼凑

给你一个任意大的整数K，我们把它拆成2进制，比如k = 13：(1101)

• 第 0 位是 1 $\rightarrow$ 跳 $2^0$ 步，更新位置。
• 第 1 位是 0 $\rightarrow$ 不跳。
• 第 2 位是 1 $\rightarrow$ 跳 $2^2$ 步，更新位置。
• 第 3 位是 1 $\rightarrow$ 跳 $2^3$ 步，更新位置。

模板代码：

// ------------------ 模板配置 ------------------
const int MAX_N = 256;  // 状态数量（本题是字符，所以是256）
const int MAX_LOG = 32; // 2^32 足够覆盖 int 范围

// dp[u][i] 表示：状态 u 经过 2^i 步后的状态
int dp[MAX_N][MAX_LOG]; 

// ------------------ 第一步：预处理 ------------------
void init_doubling(int n) { // n 是状态总数
    // 注意：i (层级) 必须在外层循环！
    // 因为算 2^i 步必须先知道所有人的 2^(i-1) 步
    for (int i = 1; i < MAX_LOG; i++) {
        for (int u = 0; u < n; u++) {
            // 核心公式：跳 2^i = 跳 2^(i-1) + 再跳 2^(i-1)
            dp[u][i] = dp[dp[u][i-1]][i-1];
        }
    }
}

// ------------------ 第二步：查询 ------------------
int query(int start_node, int k) {
    int current = start_node;
    // 遍历 k 的每一个二进制位
    for (int i = 0; i < MAX_LOG; i++) {
        // 如果 k 的第 i 位是 1 (即 (k >> i) & 1)
        if ((k >> i) & 1) {
            current = dp[current][i]; // 跳 2^i 步
        }
    }
    return current;
}

字符串编码

对于字符串的比较，等操作是比较耗费时间的，此时我们可以通过将字符串编码来将不太长的字符串编码为数字类型。

以 unsigned long long 类型为例，最长可以编13位不区分大小写的单词。

我们就以编码26位的小写字符串为例：

ll cNum = 0;
ll level = 1;
for (char c : word)
{
    cNum += (c-'a'+1)*level;
    level *= 27;
}

这里有一个易错点，至少对于我来说是，最开始我实现的代码为：

ll cNum = 0;
ll level = 1;
for (char c : word)
{
    cNum += (c-'a')*level;
    level *= 26;
}

我将字母a-z，分别映射为数字0-25。一个字母对应一个数字，这很合理。

但是此时的问题是：当输入字符串AA和A时，由于我将字符A映射为0，所以这两个字符串编码是相等的，都是0。

所以将字母编码时，我们必须从1开始编码。

附一张使用编码前后效率如图：80ms->40ms

动态规划求字符串只出现一次的数量

思考这样一个问题：

在长度为9的字符串中，至少出现一次”ccf”的字符串有多少情况？

思路：补集法+动态规划

包含至少一个CCF的情况很复杂，因为涉及到”ccf”可能出现1次，2次，以及重叠的情况。更简单的方法是：

$$\text{包含 ccf 的数量} = \text{总字符串数量} - \text{不包含任何 ccf 的数量}$$

动态规划

我们要构造一个长度为9的字符串，确保过程中永远不会出现”ccf”。我们可以根据字符串目前的后缀匹配”ccf”的进度来定义状态。

• 状态0：后缀不匹配”ccf”的任何前缀。
• 状态1：后缀匹配”c”
• 状态2：后缀匹配”cc”
• 状态3：后缀匹配”ccf”，这是我们需要避免的。

状态逻辑转移(每增加一个字符)：

1. 从状态 0 (空) 出发：
   • 加 ‘c’ $\rightarrow$ 状态 1。
   • 加其他 25 个字母 $\rightarrow$ 保持状态 0。
2. 从状态 1 (结尾 “c”) 出发：
   • 加 ‘c’ $\rightarrow$ 状态 2 (变成 “…cc”)。
   • 加其他 25 个字母 $\rightarrow$ 状态 0 (例如 “…ca”, “…cf” 都不匹配 “c” 开头)。
3. 从状态 2 (结尾 “cc”) 出发：
   • 加 ‘c’ $\rightarrow$ 保持状态 2 (变成 “…ccc”，后缀依然是 “cc”)。
   • 加 ‘f’ $\rightarrow$ 形成 “ccf”（禁忌！不能走这一步）。
   • 加其他 24 个字母 (除去 ‘c’ 和 ‘f’) $\rightarrow$ 状态 0。

递推公式：

设 $dp[i][k]$ 为长度为 $i$ 且处于状态 $k$ 的合法字符串数量。

• $dp[i][0] = dp[i-1][0] \times 25 + dp[i-1][1] \times 25 + dp[i-1][2] \times 24$
• $dp[i][1] = dp[i-1][0] \times 1 + dp[i-1][1] \times 0 + dp[i-1][2] \times 0$
• $dp[i][2] = dp[i-1][0] \times 0 + dp[i-1][1] \times 1 + dp[i-1][2] \times 1$

CCF做题有感

第一题：学会照着题目编程

CCF的第一道题一般都是非常简单的，不考察任何的算法以及优化，我们只需要照着题目的要求编程即可。题目怎么说我们就怎么写代码。

哪怕你想到了优化方法，也不要轻易尝试，这又会增加你花费在第一题上的时间。

第二题

找到背后的模型

第二题通常考察简单的算法模型，感觉基本范围都没有超过leetcode 热题100中的范围，只是有时我们可能看不出背后的算法模型。感觉像的就可以尽量关联一下。

38次第二题，是一个BFS(广度优先搜索)：

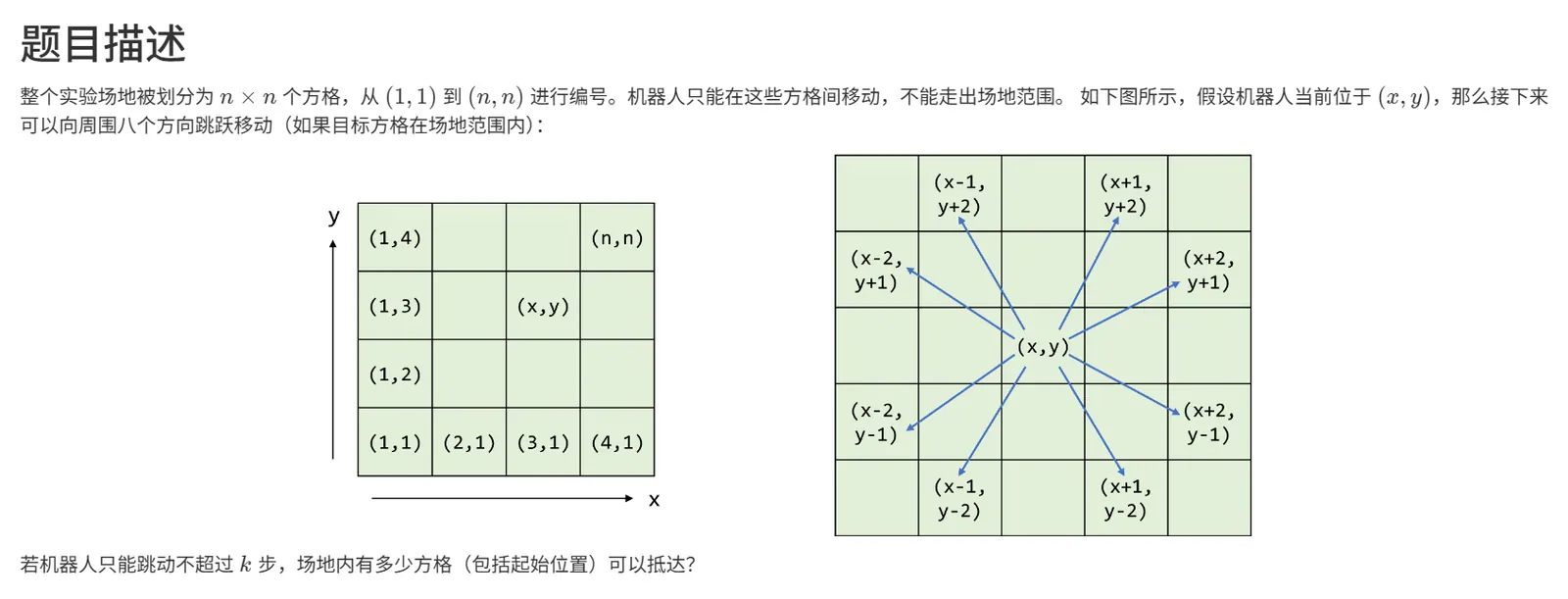
区分BFS与DFS的适用范围：

BFS(广度优先搜索)：

• 覆盖范围、最短路径、层序遍历

DFS(深度优先搜索)：

• 所有解、连通性、回溯

不过针对具体问题还是需要具体分析，建议当你考虑使用者两个算法其中一个时，不妨也仔细思考一下另一种方法。

37次第二题，是一个(不限数量)背包问题：

36次第二题，是一个前缀和与后缀和问题：

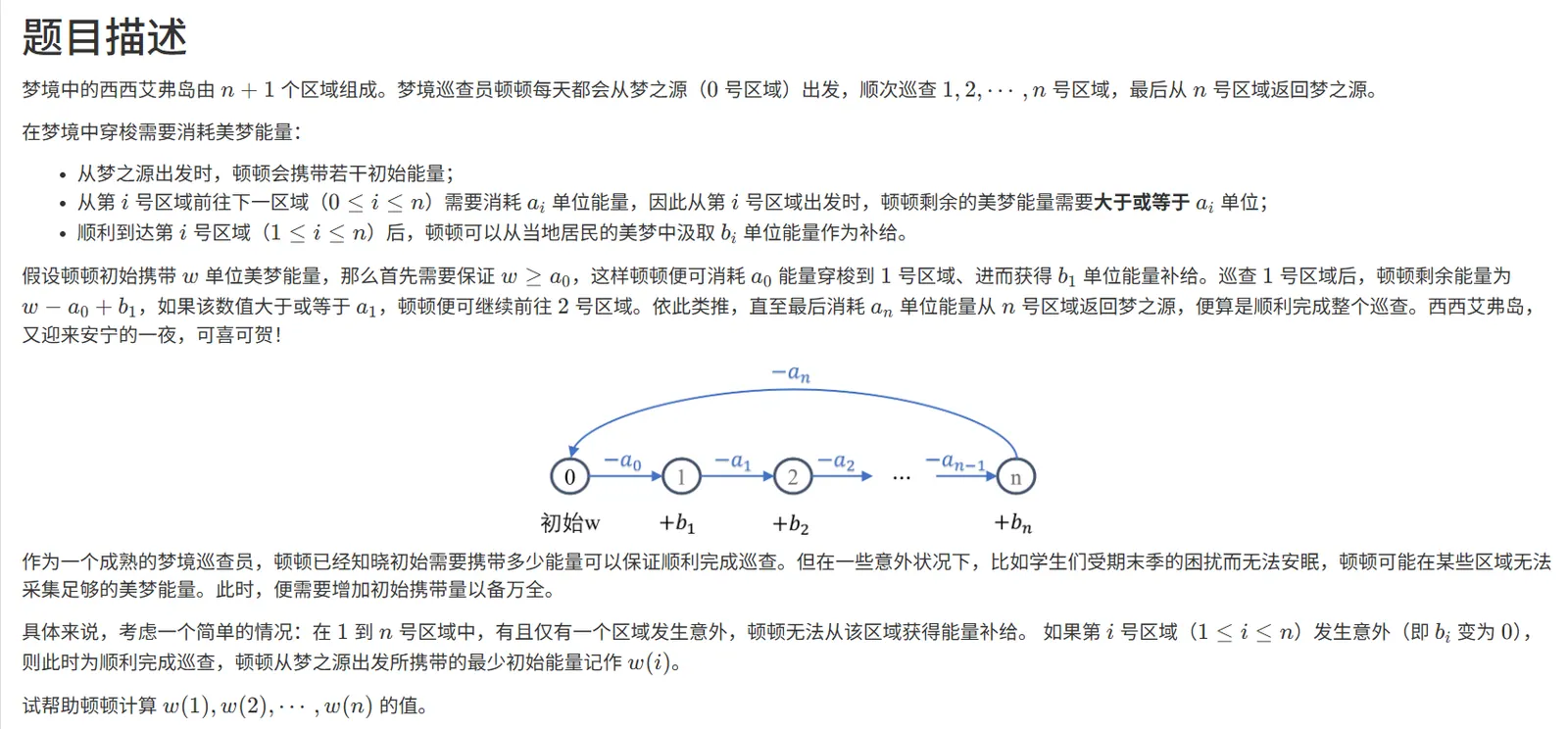
如果基础不太好这一题比较难一眼看出方法，要前提是要找到关系，携带的最少能量为：min{min(前缀中的最小值), min(后缀的最小值)- d_i }

找到CCF中的提示

CCF当前两道题的题目有相似内容时，第一题有可能会是第二题的提示，这种情况在33和34次CCF认证中均有出现。

34次CCF

34次CCF中的两题的关联很明显，分别是矩阵重塑(其一)和矩阵重塑(其二)。首先看看第一道题：

这里第一题的提示非常明显，直接提到针对矩阵重塑，我们可以将矩阵元素线性化，即使用一维数组来存储二维矩阵，最后通过n、m的值来计算二维下标。

第二题中，针对矩阵的重塑，我们即可采取第一题中的思路，使用一维数组来存储矩阵。当进行重塑操作时，我们只需要更新矩阵的n、m即可。不用实际修改数组的顺序。

33次CCF

33次的两题分别是词频统计与相似度计算。

第一题中明确提出一个思想：将英文单词转化为整数编号。

并且这里题目中明确表示每个单词最多包含10个字母，则我们可以使用将单词编码为字符串的思想，避免对进行string比较操作，而是直接使用整形，可以加快程序的速度。

会看子任务

在第30次的CCF认证中，第2题考察矩阵的运算：(感觉这题考试范围好超纲)

如果我们按照题目的给出的逻辑进行运算：

1. 先计算$A = Q \times K^T$ ,得到一个$n \times n$的矩阵。这一步复杂度是$O(n^2d)$。
2. 再计算$R = A \times V$, 得到一个$n \times d$的矩阵。这一步的复杂度也是$O(n^2d)$。
3. 最后乘上权重W。

总时间复杂度为$O(n^2d)$。如果n = 10000，d = 20，运算量约为$2 \times {10}^9$

但是我们观察子任务中的内容，n 的范围是远大于d的，也就是说不会出现d很大的矩阵，那么我们就可以通过矩阵的运算性质来改变运算顺序。

优化方案：

利用矩阵乘法的结合律 $(A \times B) \times C = A \times (B \times C)$。

我们可以先计算 $M = K^T \times V$。

1. $K^T$ 是 $d \times n$ 矩阵，$V$ 是 $n \times d$ 矩阵。计算 $M = K^T \times V$ 得到一个 $d \times d$ 的矩阵。这一步复杂度是 $O(d^2 n)$。
2. 然后计算 $Q \times M$。$Q$ 是 $n \times d$，$M$ 是 $d \times d$。这一步复杂度是 $O(n d^2)$。

总时间复杂度降低为$O(nd^2)$。速度提升非常明显。

CCF考矩阵运算，你是人啊？