每日一言

I meditate diligently every morning. The subject is Life and Love. I quit after three seconds. — Vash the Stampede from Trigun

哈希表

专业术语

1. 哈希表：一个有限的连续的地址空间，用以容纳按哈希地址存储的记录。
2. 哈希函数：记录的存储位置与它的关键字之间存在的一种对应关系。
3. 冲突：对于 $key_i$ != $key_j$ 且 i != j ，但是有 H($key_i$) == H($key_j$) 的现象，$key_i$ 占用了$key_j$ 的位置
4. 同义词： $key_i$ != $key_j$， H($key_i$) == H($key_j$)，则称为对此哈希函数的一组同义词
5. 哈希地址：根据设定的哈希函数H(key) 和处理冲突的方法确定的记录的存储位置
6. 装填因子：表中填入的记录数n和哈希表表长m之比

设计哈希表的过程：

1. 确定哈希表的地址空间范围
2. 选择合适的哈希函数
3. 设定处理冲突的方法

哈希函数的基本构造方法

直接定址法

H(key) = a * key +b

适用范围：地址集合的大小 == 关键字集合的大小

数字分析法

取关键字的若干数位作为哈希地址。

适用范围：能预先估计出全体关键字的每一位上各种数字出现的频度

平方取中法

取关键字平方后的中间几位作为哈希地址

适用范围：关键字中的每一位都有某些数字重复出现频度很高的现象。

折叠法

将关键字分割成位数相同的几部分（最后一部分的位数可以不相同），然后取这几个部分的叠加和（舍去进位）作为哈希地址。

适用范围：关键字的数字位数特别多

除留余数法

H(key) == key mod p (p<=m)

• m: 哈希表的表长
• p：最好为素数，更有利于“散列”

伪随机数法

H(key) == random(key)

选取一个用关键字作为种子的伪随机数发生器生成散列地址

适用范围：关键字长度不等时的情况。

关键字处理的常用方法

开放定址法

$$H_i = (H(\text{key}) + d_i) \mod m, \quad i=1,2,\ldots,k \quad (k \leq m-1)$$

m：哈希表的表长；$d_i$ ：增量序列

解决冲突过程：

1. 遇到冲突时，从$d_1$ 开始，依次探测H(key) + $d_i$ 的位置
2. 直到探测到一个空位置为止(循环探测)
3. 将该值放入到探测位置

两种探测方法：

1. 线性探测：$d_i = 1, 2, \ldots, m-1$
2. 二次探测：$d_i = 1^2, -1^2, 2^2, -2^2, \ldots, \pm k^2$

二次聚集

二次聚集（Secondary Clustering）是指哈希表中冲突处理方式导致的元素分布问题。它通常出现在 开放地址法 （如线性探测）中，当两个元素发生冲突时，接下来的探测序列完全相同，这可能导致多个冲突的元素聚集在相邻位置。

同时开放定址法还有一个缺点：无法直接删除一个元素。

这是因为删除元素会在数组内产生一个空桶 None ，而当查询元素时，线性探测到该空桶就会返回，因此在该空桶之下的元素都无法再被访问到，程序可能误判这些元素不存在

注意，上面我们说的是无法直接删除一个元素，这里我们介绍一种懒惰删除法。

通过一个tag标签对于元素进行标记，将元素标记为：“正常值”“删除值”两种状态

1. 查询时：正常值和删除值两种状态都表示该位置非空。
2. 插入时：遇到正常值则继续探测下一个位置，遇到删除值则可以覆盖原来的删除值。

typedef struct ElemType{
    int key;
    char tag;  //0 == NULL
               //1 == normal
               //2 == deleted
}

再哈希法

$H_i = RH_i(key) \quad i=1,2,\ldots,k \quad (k \leq m-1)$

$RH_i$ 为不同的散列函数

准备一组哈希函数，在冲突发生时，依次使用这一组函数中的下一个来再次计算哈希值，直到冲突不发生为止。

链地址法

在每个哈希地址处建立一个单链表，存储所有具有同义词的记录。

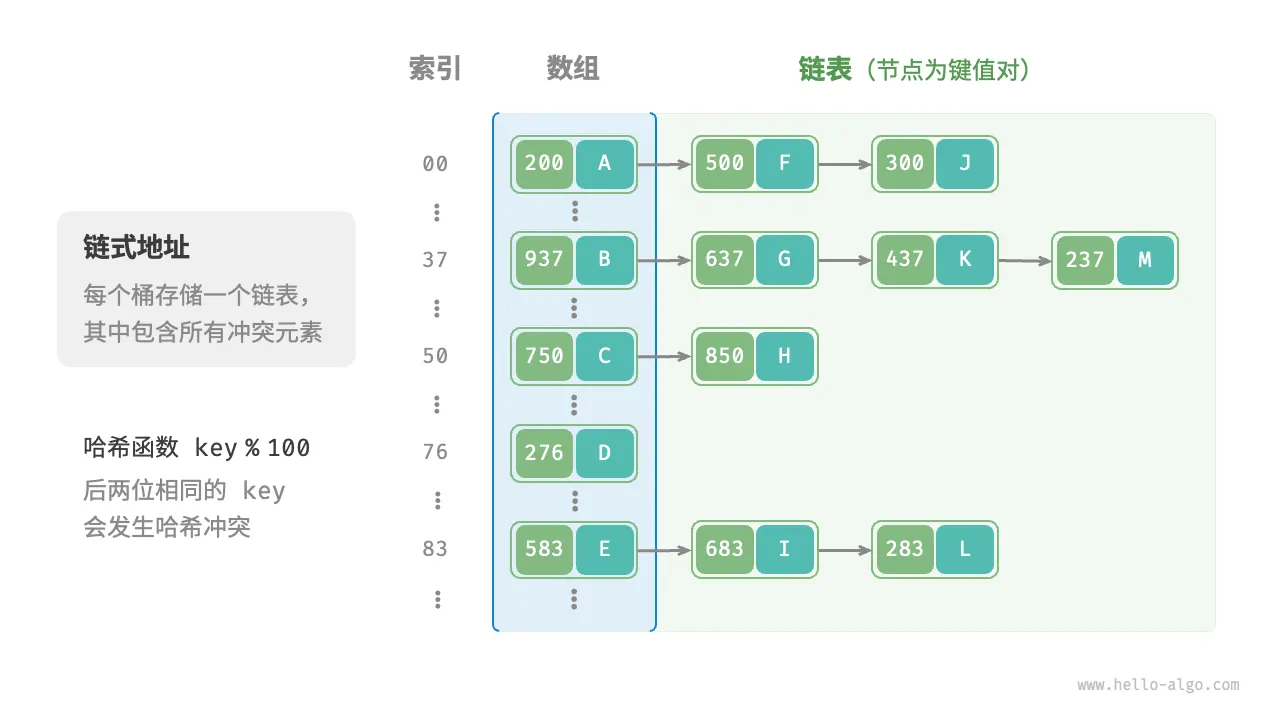
建立公共溢出区法

将所有后续出现造成冲突的元素全都按出现顺序先后放入公共溢出区中。

如上图所示，此时，168与38 出现冲突，我们将后出现的168放入公共溢出区：

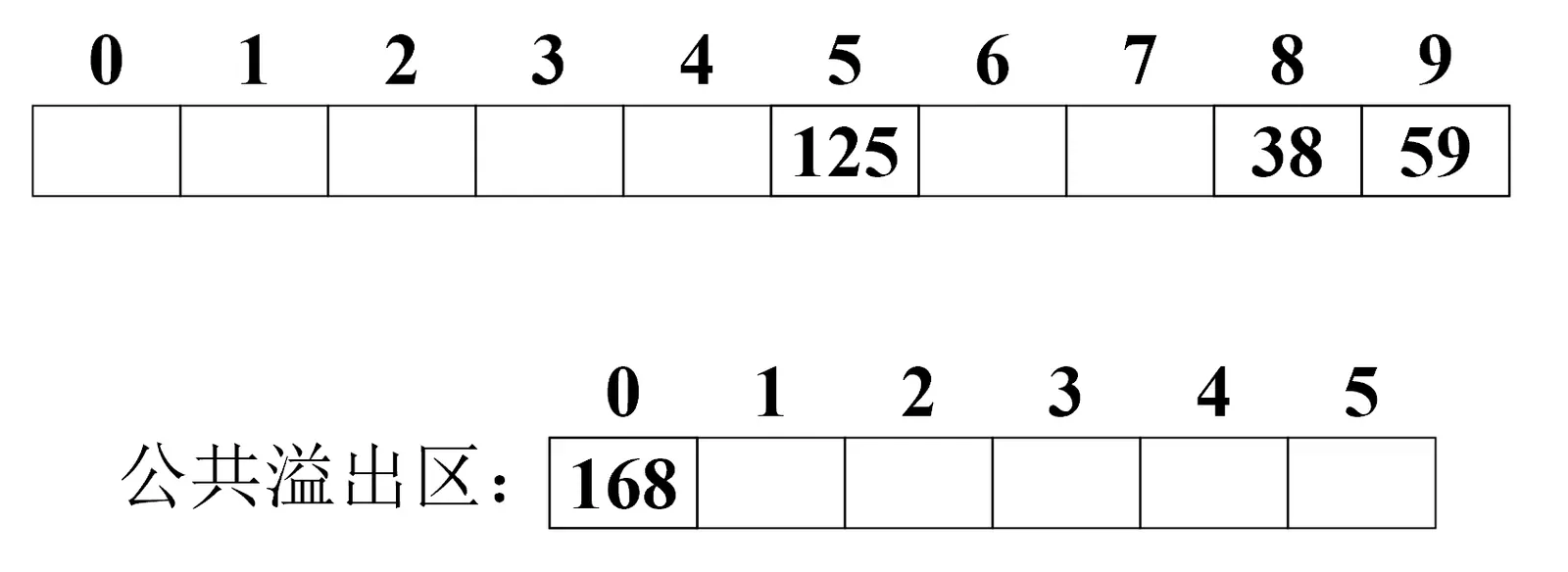
如果再次出现冲突：

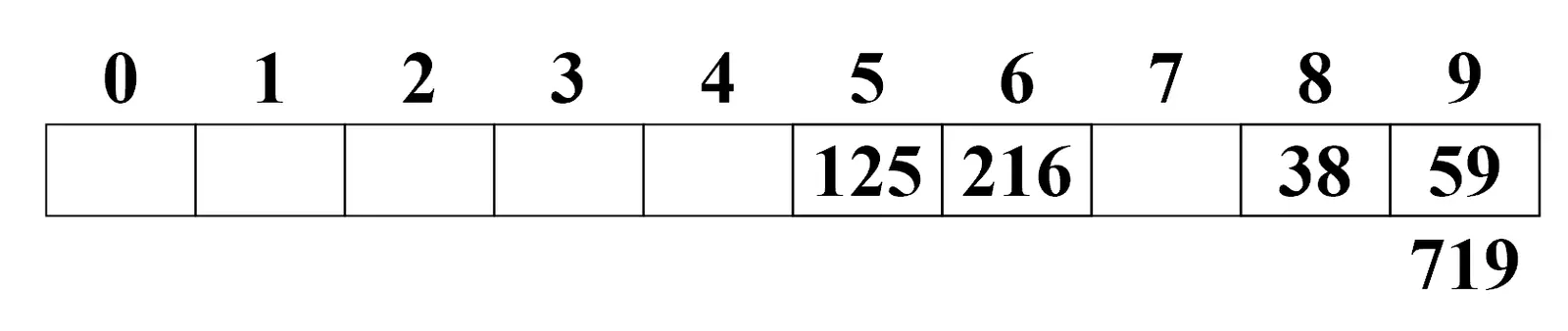
我们再次将719放入公共溢出区：

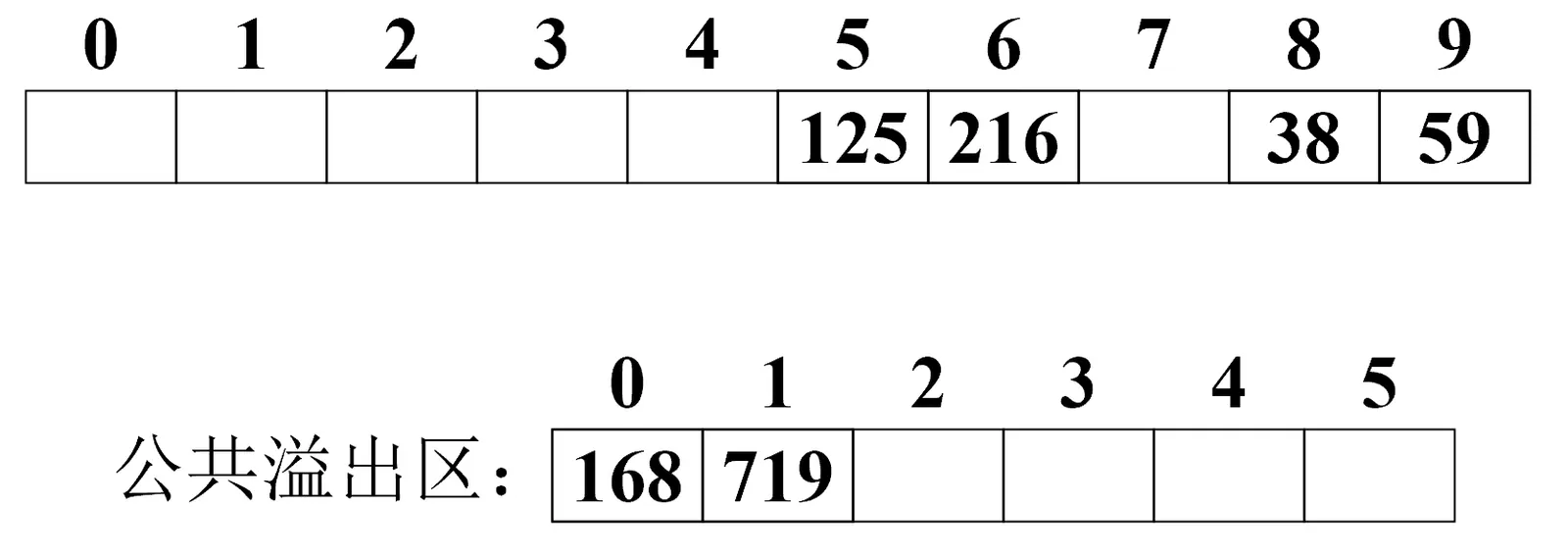
哈希表的建立、查找及其ASL分析

装填因子：

$$\alpha = \frac{表中填入的记录数}{哈希表的长度}$$

在一般情况下，$\alpha$ ↓，冲突的可能性 ↓，ASL ↓，但空间的浪费 ↑。

开放定址哈希表的存储结构

typedef struct {
    //按hashsize[sizeindex]值申请存储空间
    ElemType  *elem; 
    int  count;     // 当前数据元素个数
    int  sizeindex; // hashsize[sizeindex]为当前容量
    float  a;       //填装因子上限
} HashTable;

链地址法

存储结构：

typedef struct HashNode
{
    int key;
    struct HashNode *next;
}HashNode;

typedef struct HashTable
{
    HashNode ** elem;//二级指针，存储链表结点地址
    int count;
    int sizeindex;
    float a;
}HashTable;

初始化：

bool InitHashTable(HashTable H,int sizeindex)
{
    H.elem = new HashNode*[sizeindex]{nullptr};
    H.count = 0;
    H.a = 0;
    H.sizeindex = sizeindex;
    return true;
}

插入：

bool Insert_Hash(HashTable H,int key)
{
    int inx = Hash(key);
    HashNode* new_key = new HashNode{key,nullptr};
    if(H.elem[inx] == nullptr)
        H.elem[inx] = new_key;
    else
    {
        HashNode *p = H.elem[inx],*ap = p;
        while(p != nullptr && p->key!= key)
        {
            ap = p;
            p = p->next;
        }
        if(p == nullptr)
        {
            ap->next = new_key;//不存在，新插入
            return true;
        }
        else
        {
            return true;//已经存在
        }
    }
    return true;
}

删除：

bool dalete_Hash(HashTable H,int key)
{
    int inx = Hash(key);
    if(H.elem[inx] == nullptr)
        return true;//原本不存在
    else
    {
        HashNode *p = H.elem[inx],*ap = p;
        while(p != nullptr && p->key!= key)
        {
            ap = p;
            p = p->next;
        }
        if(p == nullptr)//原本不存在
        {
            return true;
        }
        else//原本存在，删除掉
        {
            ap->next = ap->next->next;
            delete p;
            return true;
        }
    }
    return true;  
}