动手学习深度学习————多层感知机

在过去几年里，深度学习给世界带来惊喜，推动了计算机视觉、自然语言处理、自动语音识别、强化学习和统计建模等领域的快速发展。

感知机

给定输入x，权重w，和偏移b，感知机输出：

$$
o = \sigma \left( \langle \mathbf{w}, \mathbf{x} \rangle + b \right)
$$

$$
\sigma(x) = \begin{cases} 1 & \text{if } x > 0 \ -1 & \text{otherwise} \end{cases}
$$

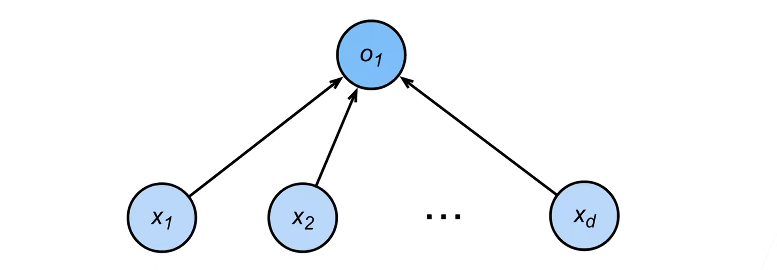
这是一个二分类的问题：输出1/-1

• 回归问题：输出一个实数；而二分类问题输出一个类别
• Softmax回归：多分类问题，输出概率

感知机的训练算法

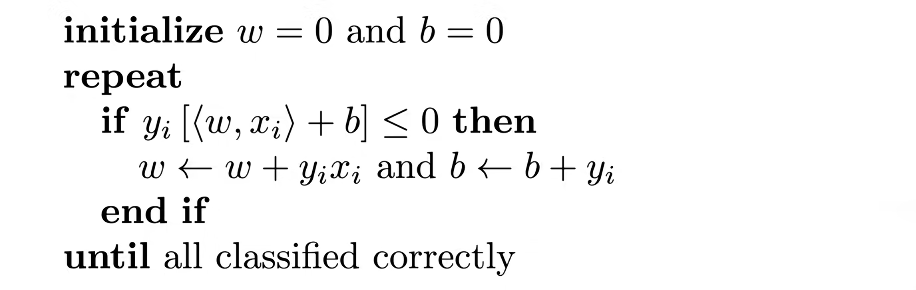
初始化：将权重向量$w$和偏置$b$都初始化为0。

循环：算法会不断循环遍历训练数据，直到所有的样本都被正确的分类。

判断错误分类：

$$
y_i [\langle w, x_i \rangle + b] \leq 0
$$

• 这里的$y_i$是真实的标签(为+1或-1)
• $\langle w, x_i \rangle + b$ 是模型对样本$x_i$的预测输出值
• 含义：如果$y_i$和预测值的符号相反(乘积为负)，或者预测值为0，说明分类错误。

更新规则：

$$
w \leftarrow w + y_i x_i
$$

$$
b \leftarrow b + y_i
$$

• 含义：当发现一个错误样本时，利用该样本的信息来调整权重。
• 如果是正样本($y=1$)被误判为负，就加上$x$(让$w$向$x$的方向靠近)
• 如果是负样本($y=-1$)被误判为正，就减去$x$(让$w$远离$x$)

更新规则的数学逻辑：

感知机的预测完全取决于内积 $\langle w, x \rangle$ 的正负（为了简化，我们先忽略偏置 $b$）。

• 当 $y=1$（正样本）被误判：此时目前的 $\langle w, x \rangle \le 0$。我们希望这个值 变大 （最好变成正数）。如果我们更新 $w_{new} = w + x$，那么新的内积为：

  $$
  \langle w+x, x \rangle = \langle w, x \rangle + \langle x, x \rangle = \langle w, x \rangle + |x|^2
  $$

  因为 $|x|^2$ 永远是正数，所以更新后的内积 一定会增加 。这让该样本在下次预测时更趋向于被判定为正。

• 当 $y=-1$（负样本）被误判：此时目前的 $\langle w, x \rangle \ge 0$。我们希望这个值变小（最好变成负数）。如果我们更新 $w_{new} = w - x$，新的内积为：

  $$
  \langle w-x, x \rangle = \langle w, x \rangle - |x|^2
  $$

  内积一定会减小，从而让该样本更趋向于被判定为负。

优化视角解释

以上的感知机训练算法，等价于使用批量大小为1的梯度下降，并使用如下的损失函数：

$$
\ell(y, \mathbf{x}, \mathbf{w}) = \max(0, -y\langle \mathbf{w}, \mathbf{x} \rangle)
$$

理解这个公式：

• 如果分类正确：$y\langle \mathbf{w}, \mathbf{x} \rangle > 0$，那么 $-y\langle \mathbf{w}, \mathbf{x} \rangle < 0$，经过 $\max(0, \dots)$ 后损失为 0 。此时梯度为 0，参数 不更新 。
• 如果分类错误： $y\langle \mathbf{w}, \mathbf{x} \rangle < 0$**，那么 **$-y\langle \mathbf{w}, \mathbf{x} \rangle > 0$，损失为正。

更新规则：当分类错误时，损失函数对 $w$ 求导（梯度）是 $-yx$。

代入 SGD 更新公式（假设学习率为 1）：

$$
w_{new} = w_{old} - \text{learning_rate} \times \text{gradient}
$$

$$
w_{new} = w_{old} - 1 \times (-yx) = w_{old} + yx
$$

感知机收敛定理

• 数据半径 $r$ ：假设所有的输入数据 $x$ 都分布在一个半径为 $r$ 的圆（或高维球体）内。即数据的大小（范数）是有界的。
• 余量 $\rho$ (Margin) ：这代表了正负两类样本之间“最宽”的那条缝隙。

感知机的步数上限：

$$
\text{最大步数} \le \frac{r^2 + 1}{\rho^2}
$$

感知机的问题

感知机不能拟合XOR函数，它只能产生线性分割面。导致了第一次AI的寒冬。

XOR问题：无法使用一条直线，将两种颜色的球完全分开。

多层感知机

上面我们提到单层感知机模型无法解决非线性问题，而引入隐藏层可以解决这一问题。

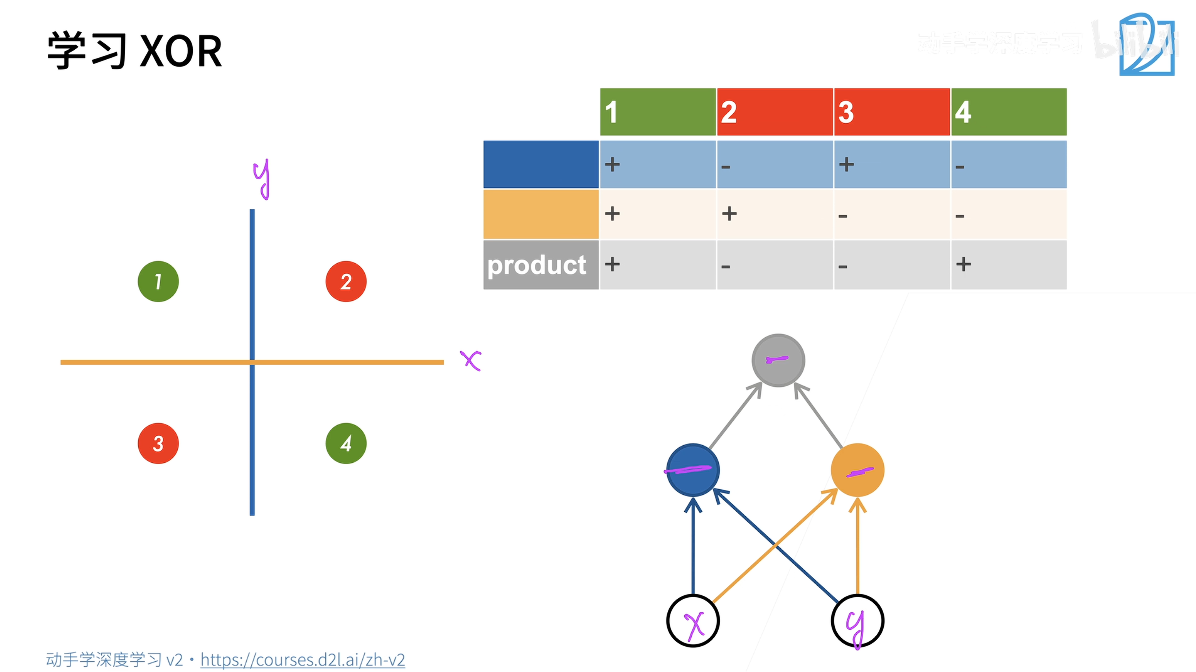
在这个问题中，隐藏层相当于两条辅助线，这就好比我们在做特征工程，我们将原始复杂的分类任务拆解成了两个简单的子任务：

• 蓝色特征：
  • 网络学会的第一条规则是区分左右(即x轴的符号)
  • 左边为 + ，右边为 - ，这对应图中的蓝色竖线
• 黄色特征：
  • 网络学会的第二条规则是区分上下(即y轴的符号)
  • 上边为 + ， 下边为 - ，这对应了图中的黄色横线。

现在，我们有了两个新的特征（蓝色和黄色）。神经网络的输出层（Output Layer）所做的工作，就是将这两个特征进行 非线性组合 （在这里可以理解为乘法或异或逻辑）：

$$
公式逻辑：Product = Blue × Yellow
$$

对应到神经网络架构，这就是一个最简单的多层感知机(MLP)：

1. 输入层(x, y)：也就是原始数据的坐标。
2. 隐藏层：这里有两个神经元：
   • 一个负责学习蓝色规则
   • 一个负责学习黄色规则
3. 输出层：接收隐藏层信号，完整最终的逻辑判断

单隐藏层

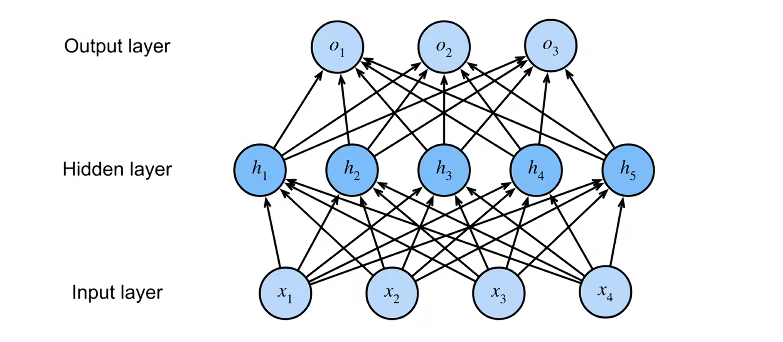
• 隐藏层的大小是一个超参数。

输入输出的大小都是由数据和类别决定的。

单分类

核心组件

单分类指输出为一个标量的情况。

输入层：

• $\mathbf{x} \in \mathbb{R}^n$：代表输入是一个n维向量。

隐藏层：

• $\mathbf{W}_1 \in \mathbb{R}^{m \times n}$：这是第一层的权重矩阵。它将n维输入映射到m维空间。
• $\mathbf{b}_1 \in \mathbb{R}^m$：偏置项，对应隐藏层的m个神经元。

输出层：

• $\mathbf{w}_2 \in \mathbb{R}^m, b_2 \in \mathbb{R}$：单输出的情况，$\mathbf{w}_2$是一个一维向量。

数学表达式

1. 隐藏层计算：

$$
\mathbf{h} = \sigma(\mathbf{W}_1\mathbf{x} + \mathbf{b}_1)
$$

• 这里先进行线性变换$\mathbf{W}_1\mathbf{x} + \mathbf{b}_1$
• $\sigma$(激活函数)：按元素做运算的函数。后续细讲。

2. 输出层计算：

$$
o = \mathbf{w}_2^T \mathbf{h} + b_2
$$

• 这是将隐藏层提取到的特征h进行加权求和，得到最终的预测值。

激活函数 Activation function

激活函数通过计算加权和并加上偏置来确定神经元是否应该被激活，它们将输入信号转换为输出的可微运算。大多数激活函数都是非线性的。 由于激活函数是深度学习的基础。

为什么需要激活函数

简单来说，如果没有激活函数，再深的网络也只是一层。

假设我们有一个两层的神经网络，但没有激活函数。

• 第一层输出：$\mathbf{h} = \mathbf{W}_1 \mathbf{x} + \mathbf{b}_1$
• 第二层输出：$\mathbf{o} = \mathbf{W}_2 \mathbf{h} + \mathbf{b}_2$

我们将第一层代入第二层：

$$
\mathbf{o} = \mathbf{W}_2 (\mathbf{W}_1 \mathbf{x} + \mathbf{b}_1) + \mathbf{b}_2
$$

$$
\mathbf{o} = (\mathbf{W}_2 \mathbf{W}_1) \mathbf{x} + (\mathbf{W}_2 \mathbf{b}_1 + \mathbf{b}_2)
$$

如果我们令 $\mathbf{W}_{new} = \mathbf{W}_2 \mathbf{W}_1$ 且 $\mathbf{b}_{new} = \mathbf{W}_2 \mathbf{b}_1 + \mathbf{b}_2$，那么公式就变成了：

$$
\mathbf{o} = \mathbf{W}{new} \mathbf{x} + \mathbf{b}{new}
$$

结论： 无论你堆叠多少层，只要是线性的，它们最终都可以合并成一个单一的线性层。这意味着你的“深度”网络在表达能力上和最简单的感知机没有任何区别，无法处理复杂的任务。

激活函数的作用：它像一个”开关”或”过滤器”，决定了神经元的哪些信息应该传递到下一层。它引入了非线性，让网络能够拟合出复杂的边界。

• 万能近似定理：只要神经网络拥有至少一个包含足够多神经元的隐藏层，并配合非线性激活函数，它就可以以任意精度拟合闭区间内的连续函数。

常见的激活函数

ReLU函数

修正线性单元(Rectified linear unit, ReLU)，这是最受欢迎的激活函数。

$$
\text{ReLU}(x) = \max(x, 0)
$$

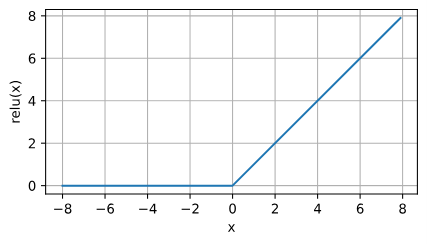
ReLU导数的图像：

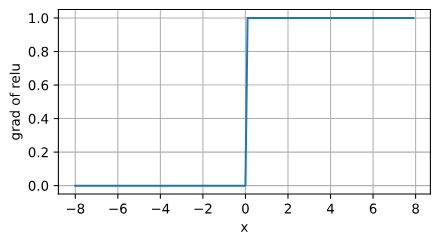
注意：当输入值精确等于0时，ReLU函数不可导。在此时，我们默认使用左侧的导数。我们可以忽略这种情况，因为输入可能永远都不会是0。 这里引用一句古老的谚语，“如果微妙的边界条件很重要，我们很可能是在研究数学而非工程”， 这个观点正好适用于这里。

优点：

• 实现简单。
• 无需计算指数，计算速度快。
• 求导表现好

sigmoid函数

sigmoid函数将输入变换为区间(0, 1)上的输出。

$$
\text{sigmoid}(x) = \frac{1}{1 + \exp(-x)}.
$$

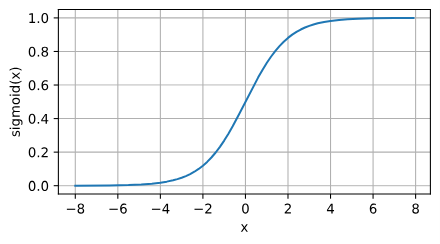
sigmoid函数的导数：

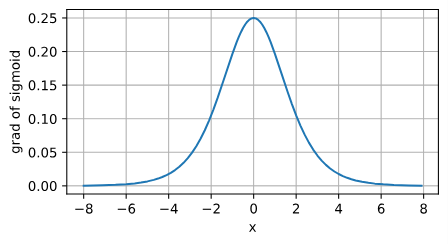
针对梯度下降的学习时，sigmoid是一个自然的选择，因为他是一个平滑的、可微的阈值单元近似。然而，sigmoid在隐藏层中已经较少使用， 它在大部分时候被更简单、更容易训练的ReLU所取代。

tanh函数

与sigmoid函数类似， tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。 tanh函数的公式如下：

$$
\tanh(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}.
$$

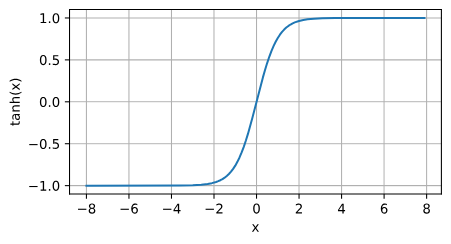
tanh函数的导数：

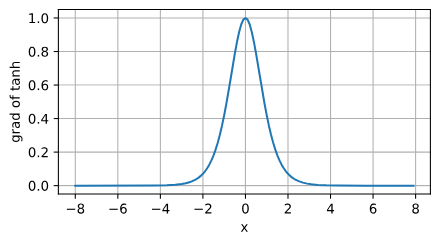
tanh函数和sigmoid函数计算都比较复杂，在深度学习中算力是宝贵的资源，所以一般情况下都选择使用ReLU函数。

多类分类

$$
y_1, y_2, \dots, y_k = \text{softmax}(o_1, o_2, \dots, o_k)
$$

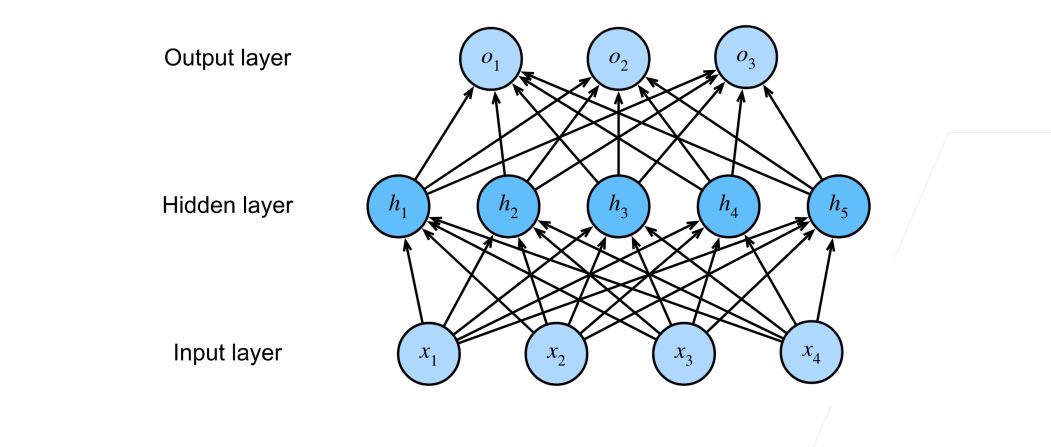
输入层：$\mathbf{x} \in \mathbb{R}^n$

隐藏层：$ \mathbf{W}_1 \in \mathbb{R}^{m \times n}, \mathbf{b}_1 \in \mathbb{R}^m$

输出层：$ \mathbf{W}_2 \in \mathbb{R}^{m \times k}, \mathbf{b}_2 \in \mathbb{R}^k$

这里$\mathbf{W}_2$不再是一个向量，而是一个矩阵$\mathbb{R}^{m \times k}$。它把m维的隐藏特征映射到k个类别的评分上。

计算公式：

• 隐藏层激活：

$$
\mathbf{h} = \sigma(\mathbf{W}_1 \mathbf{x} + \mathbf{b}_1)
$$

• 输出层线性变换：

$$
\mathbf{o} = \mathbf{W}_2^T \mathbf{h} + \mathbf{b}_2
$$

• 最终输出：

$$
\mathbf{y} = \text{softmax}(\mathbf{o})
$$

多类分类与softmax回归没有本质区别，只是增加了隐藏层。

多隐藏层

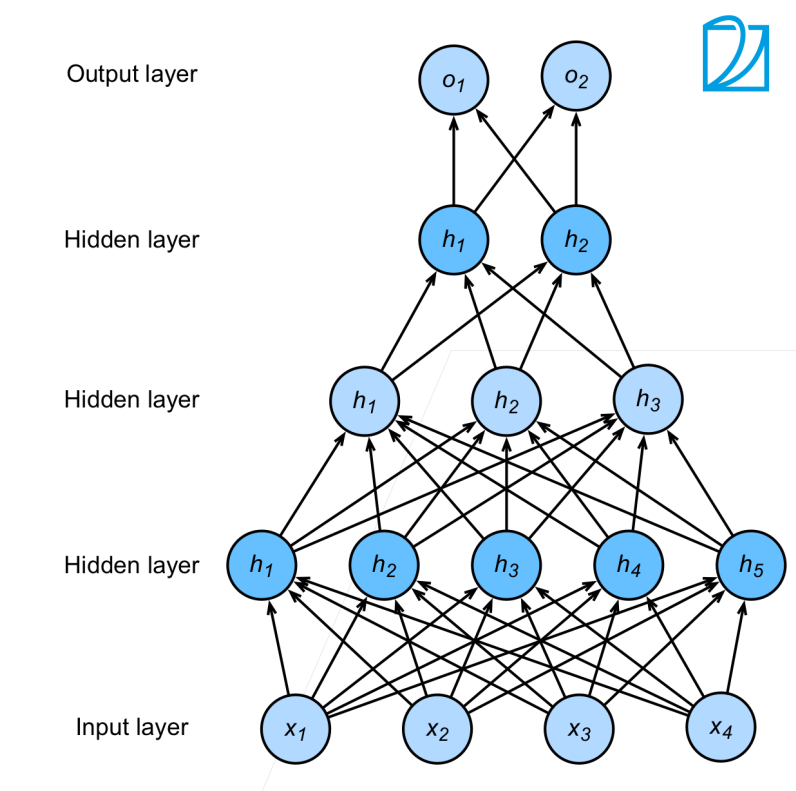
计算公式：

$$
\begin{aligned}
\mathbf{h}_1 &= \sigma(\mathbf{W}_1 \mathbf{x} + \mathbf{b}_1) \
\mathbf{h}_2 &= \sigma(\mathbf{W}_2 \mathbf{h}_1 + \mathbf{b}_2) \
\mathbf{h}_3 &= \sigma(\mathbf{W}_3 \mathbf{h}_2 + \mathbf{b}_3) \
\mathbf{o} &= \mathbf{W}_4 \mathbf{h}_3 + \mathbf{b}_4
\end{aligned}
$$

针对多层感知机，我们需要设计其中的超参数：

• 隐藏层数
• 每层隐藏层的大小