动手学习深度学习——线性神经网络
不到10年时间,人工智能革命已从研究实验室席卷至广阔的工业界,并触及我们日常生活的方方面面。
线性回归
线性模型
一个实际的线性模型如下:(经典买房)
模型假设:
- 假设1:影响房价的关键因素是卧室个数、卫生间个数和居住面积,分别记为:$x_1$、$x_2$、$x_3$。
- 假设2:成交价是关键因素的加权和:
$$
y = w_1x_1 + w_2x_2 + w_3x_3 + b
$$
更广泛的定义:
- 给定n维输入:$\mathbf{x} = [x_1, x_2, \dots, x_n]^T$
- 线性模型有一个n维权重和一个标量偏差:
$$
\mathbf{w} = [w_1, w_2, \dots, w_n]^T, \quad b
$$ - 输出是输入的加权和:
$$
y = w_1x_1 + w_2x_2 + \dots + w_nx_n + b
$$ - 向量版本(简化表达):$y = \langle \mathbf{w}, \mathbf{x} \rangle + b$
$\langle \mathbf{w}, \mathbf{x} \rangle$ 表示向量 $\mathbf{w}$ 和 $\mathbf{x}$ 的 内积 ,在欧几里得空间中它等同于点积 $\mathbf{w}^T\mathbf{x}$。
线性模型可以看做是单层神经网络:
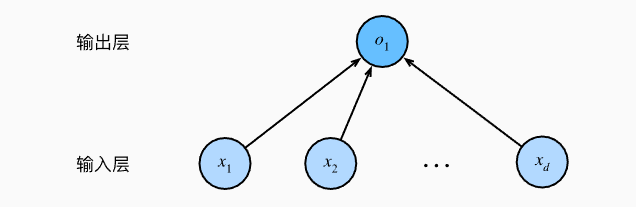
- 输入的维度为:d
- 输出的维度为:1
- 每个箭头表示一个权重w。
衡量预估质量
比较真实值和预估值,例如房屋售价和估价。
假设y是真实值,$\hat{y}$ 是估计值。
一个常见的损失为:(平方损失)
$$
\ell(y, \hat{y}) = \frac{1}{2}(y - \hat{y})^2
$$
训练数据
收集一些数据点来决定参数值(权重和偏差),例如过去6个月卖的房子。这些数据就称为训练数据。
训练数据通常越多越好。
假设我们有n个样本记为:
$$
\mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_n]^T \quad \mathbf{y} = [y_1, y_2, \dots, y_n]^T
$$
参数学习
根据求所有估计值的损失平均值,我们得到损失函数:

计算目标:找到一个w,b的对应值,最小化损失函数:
$$
\mathbf{w}^, \mathbf{b}^ = \underset{\mathbf{w}, b}{\arg\min} \ell(\mathbf{X}, \mathbf{y}, \mathbf{w}, b)
$$
$\mathbf{w}^, \mathbf{b}^$ :星号通常表示 最优值 ,即让损失函数达到最小的参数组合。
基础优化方法
梯度下降
步骤:
挑选一个随机初始值$w_0$
重复迭代参数t = 1, 2, 3
$$
\mathbf{w}t = \mathbf{w}{t-1} - \eta \frac{\partial \ell}{\partial \mathbf{w}_{t-1}}
$$- 沿梯度方向将增加损失函数值
- 学习率$\eta$:步长的超参数
超参数:需要人为设置的参数。
小批量随机梯度下降
我们很少直接使用梯度下降法,因为在整个训练集上计算梯度代价很大。一个深度神经网络模型可能需要数分钟至数小时才能计算一次梯度。
我们可以随机采样b个样本$i_1, i_2, …, i_b$来近似损失:
$$
\frac{1}{b} \sum_{i \in I_b} \ell(\mathbf{x}_i, y_i, \mathbf{w})
$$
b是批量大小,也是一个重要的超参数,
批量大小的设置准则:
- 不能太小:每次计算量太小,不适合并行来最大利用计算资源。
- 不能太大:内存消耗增加,浪费计算。
小批量随机梯度下降是深度学习框架默认的求解算法
线性回归的从零实现
导入包:
1 | |
生成数据集
为了简单起见,我们将根据带有噪声的线性模型构造一个人造数据集。人造数据集的一个好处是我们知道真实的参数w和b。
我们使用线性模型参数$\mathbf{w} = [2, -3.4]^T, \quad b = 4.2$和噪声项$\epsilon$生成数据集以及标签:
$$
\mathbf{y} = \mathbf{X}\mathbf{w} + b + \epsilon
$$
生成数据集函数:
1 | |
torch.matmul():是一个高度优化的、全能型的乘法函数。
- 处理一维向量 :如果两个输入都是一维的,它计算的是 点积 。
- 处理二维矩阵 :行为与
torch.mm一致。- 处理高维张量(广播机制) :如果输入维度大于 2(例如 Batch 数据 $[B, N, M]$),它会执行 批处理矩阵乘法 。它会保持前面的 Batch 维度不变,只对最后两个维度进行矩阵乘法。
生成数据:


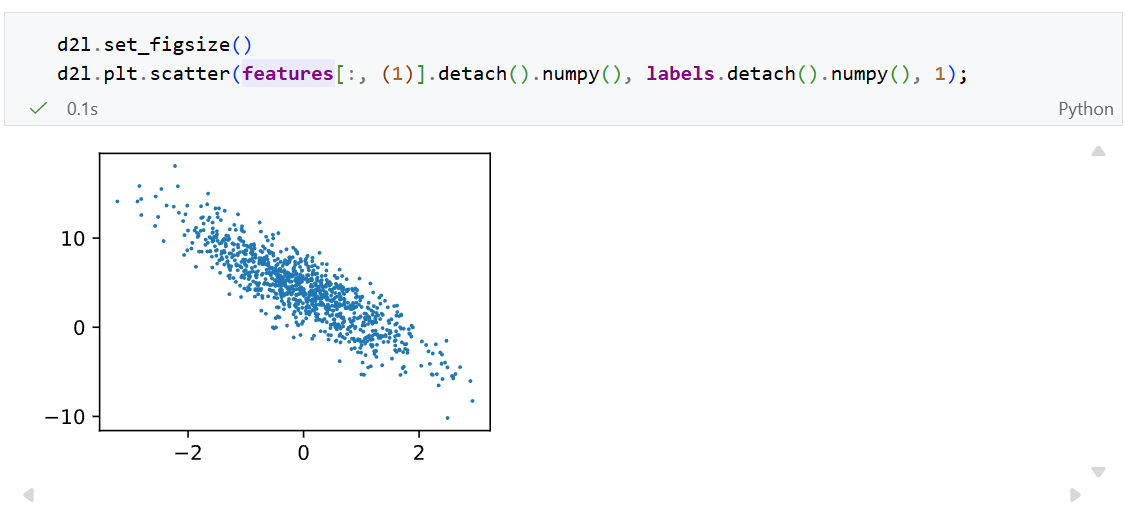
其中第二个特征 features[: , 1] 和 labels的散点图,可以直观观察到两者之间的线性关系:
读取数据集
训练模型时需要对数据集进行遍历,每次抽取一小批样本,并使用它们来更新我们的模型。由于这个过程是训练机器学习算法的基础,所以有必要定义一个函数, 该函数能打乱数据集中的样本并以小批量方式获取数据。
我们定义一个 data_iter函数,该函数接受批量大小、特征矩阵和标签向量作为输入,生成大小为batch_size的小批量。每个小批量包含一组特征和标签:
1 | |
当我们运行迭代时,我们会连续地获得不同的小批量,直至遍历完整个数据集。 上面实现的迭代对教学来说很好,但它的执行效率很低,可能会在实际问题上陷入麻烦。 例如,它要求我们将所有数据加载到内存中,并执行大量的随机内存访问。 在深度学习框架中实现的内置迭代器效率要高得多, 它可以处理存储在文件中的数据和数据流提供的数据。
初始化模型参数
我们将w随机初始化为满足(0, 0.01)正态分布的向量
将b初始化为0标量。

定义模型
作用:将模型的输入和参数同模型的输出关联起来。
线性模型定义:
1 | |
定义损失函数
损失函数我们使用均方损失:
1 | |
我们将真实值
y的形状转为和预测y_hat相同的形状。
定义优化算法
优化算法我们选择使用小批量随机梯度下降法。
下面的函数实现小批量随机梯度下降更新。该函数接受模型参数集合、学习速率和批量大小作为输入。
1 | |
为什么要除以batch_size?
在《动手学深度学习》的实现中,损失函数(Loss)是直接求和(
l.sum())而不是取平均。这意味着:
- 如果
batch_size是 10,param.grad就是 10 个样本梯度的总和。- 如果
batch_size是 100,param.grad就是 100 个样本梯度的总和。
为了保证无论batch_size选多大,我们每一步更新的“力度”是基本稳定的,我们需要除以batch_size来获得 平均梯度 。
训练
在每次迭代中,
- 我们取一小批量训练样本,并通过我们的模型来获得一组预测。
- 计算损失
- 反向传播,存储每个参数的梯度
- 调用优化算法sgd来更新模型参数
1 | |
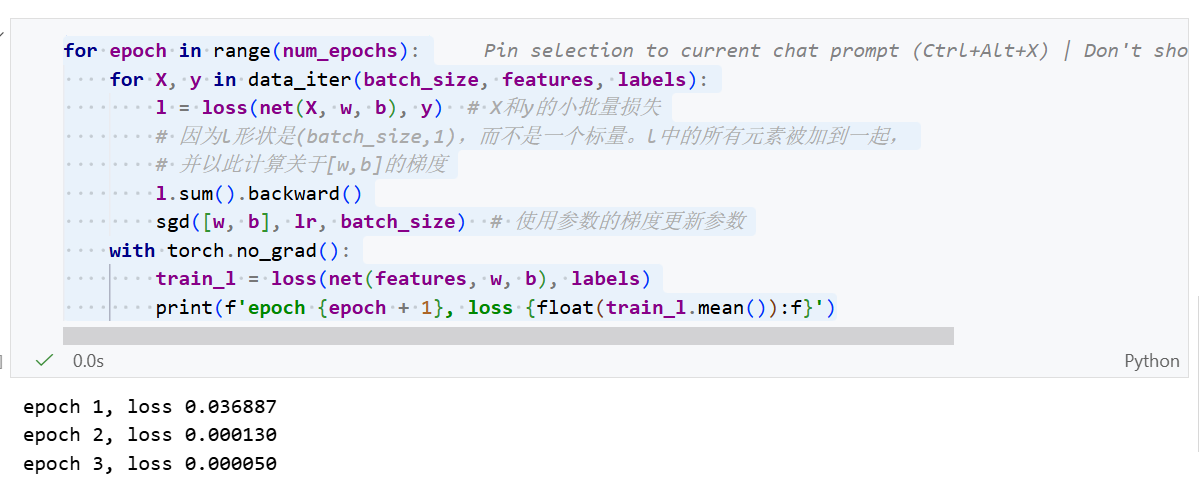
训练效果:
线性回归的简介实现
使用深度学习框架来简洁地实现线性回归模型。
生成数据集
生成数据集没有什么不同,与之前从0实现完全一致,不过我们额外导入了一些包:
1 | |
我们可以使用框架中现有的API来读取数据。
1 | |
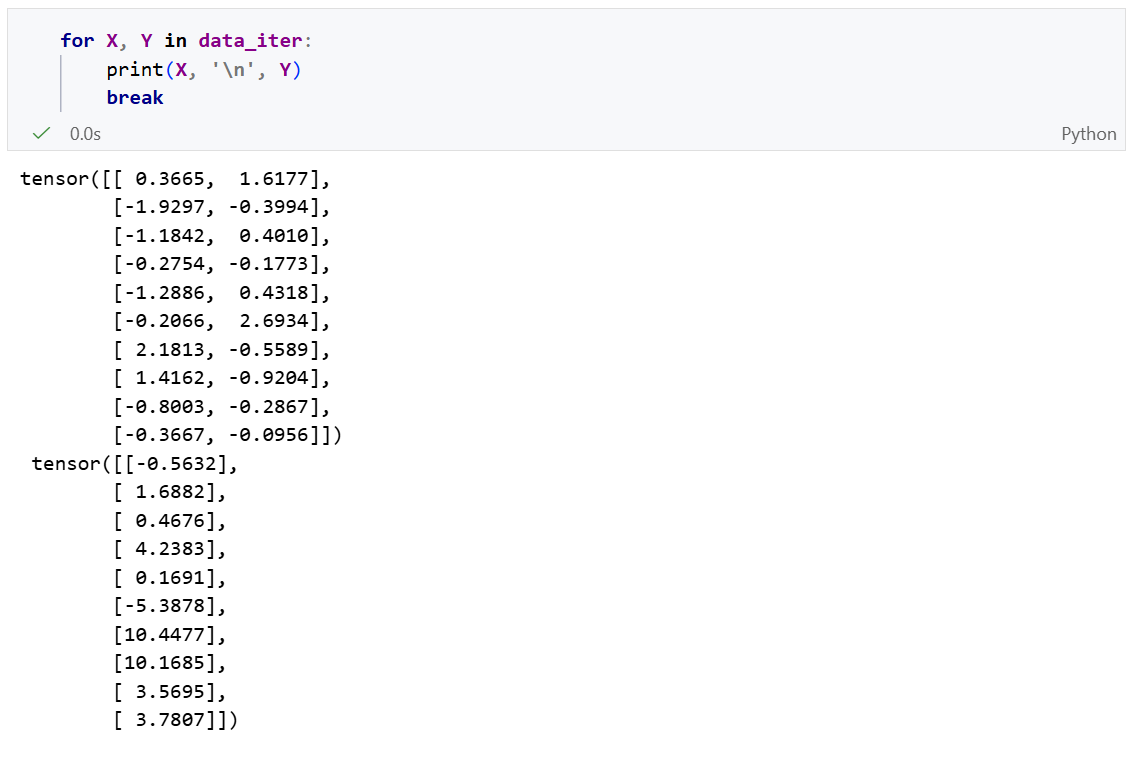
我们可以尝试通过迭代器获取数据第一项:等价于 next(iter(data_iter))
定义模型
对于标准的深度学习模型,我们可以使用框架的预定义好的层。这使我们只需要关注使用哪些层来构造模型,而不必关注层的实现细节。
1 | |
Sequential类将多个层串联到一起。当给定输入数据时,Sequential实例将数据传入第一层,然后将第一层的输出作为第二层的输入,以此类推。
在上面的例子中,我们的模型只包含一个层,因此实际上不需要Sequential。但是由于以后的模型都是多层的,这里使用Sequential会让我们熟悉标准流水线。
初始化模型参数
在使用net之前,我们需要初始化模型参数。在这里为线性模型中的权重和偏置。
1 | |
定义损失函数
计算均方误差使用MSELoss类,也被称为平方$L_2$范数。默认情况下,它返回所有样本损失的平均值。
1 | |
定义优化算法
小批量随机梯度下降算法是一种优化神经网络的标准工具, PyTorch在 optim模块中实现了该算法的许多变种。
当我们实例化SGD实例时,我们需要指定优化的参数以及优化算法所需要的超参数字典。
1 | |
训练
在每个迭代周期里,我们将完整遍历一次数据集(train_data), 不停地从中获取一个小批量的输入和相应的标签。 对于每一个小批量,我们会进行以下步骤:
- 通过net(X)生成预测并计算损失l(前向传播)
- 通过反向传播来计算梯度
- 通过调用优化器来更新模型参数
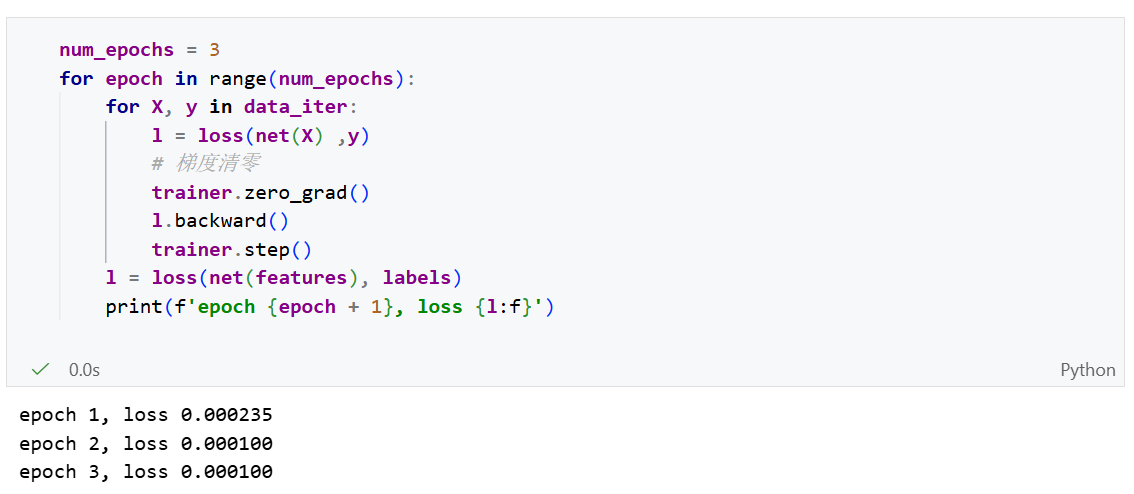
softmax回归
softmax回归虽然名字叫做回归,但其实是一个分类问题。
回归:
- 单连续数值输出
- 自然区间R
- 跟真实值的区别作为损失
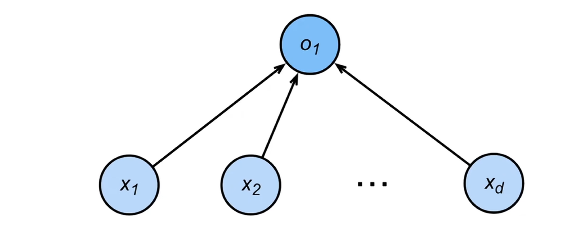
分类:
- 通常多个输出
- 输出i是预测为第i类的置信度
- 网络架构:
$$
\begin{align*}
o_1 &= x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1, \
o_2 &= x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_2, \
o_3 &= x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_3.
\end{align*}
$$
从回归到多类分类
多分类问题我们需要对类别进行编码。常见的编码方式有一位有效编码:
$$
\mathbf{y} = [y_1, y_2, \dots, y_n]^\top
$$
$$
y_i =
\begin{cases}
1 & \text{if } i = y \
0 & \text{otherwise}
\end{cases}
$$
如果真实的类别为第i个,则$y_i = 1$,其他类别均为0
使用均方损失训练
最大值最为预测:$\hat{y} = \mathop{\mathrm{argmax}}\limits_{i} o_i$
训练目标:需要更置信的识别正确类
$$
o_y - o_i \geq \Delta(y, i)
$$
softmax
神经网络直接计算出来的输出可以是任意实数(有正有负,有大有小),很难直接解释为概率。
为了解决,引入Softmax函数:
$$
\hat{\mathbf{y}} = \mathrm{softmax}(\mathbf{o})
$$
$$
\hat{y}_i = \frac{\exp(o_i)}{\sum_k \exp(o_k)}
$$
作用:
- 非负:通过指数函数 $\exp(o_i)$,将所有输出变成正数。
- 和为1:通过除以所有项的总和 $\sum_k \exp(o_k)$,对数据进行归一化,使得所有类别的预测概率加起来等于 1。
其中概率$y$和$\hat{y}$的区别作为损失。
交叉熵
交叉熵是信息论中的概念:用于衡量两个概率分布的相似度:
公式:
$$
H(\mathbf{p}, \mathbf{q}) = \sum_i - p_i \log(q_i)
$$
- $\mathbf{p}$ (真实分布): 代表事实。例如这张图是猫,$\mathbf{p}$ 就是 $[1, 0, 0]$(猫的概率是1)。
- $\mathbf{q}$ (预测分布): 代表模型的猜测。例如模型觉得是猫的概率是 0.7,$\mathbf{q}$ 就是 $[0.7, 0.2, 0.1]$。
直观理解: 如果预测 ($\mathbf{q}$) 越接近真实 ($\mathbf{p}$),这个交叉熵的值就越小;反之越大。
损失函数
我们通过计算信息熵作为损失函数:
$$
l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{i} y_i \log \hat{y}_i = - \log \hat{y}_y
$$
假设正确答案是第 $i$ 类,那么只有 $y_y = 1$,其他的 $y_i$ 全是 0。
训练模型时,我们只需要关注 模型对“正确类别”预测了多大的概率 。如果正确类别的预测概率越高(接近1),$-\log$ 值就越小(损失越小)。
梯度
其梯度就是真实概率和预测概率的区别:
$$
\frac{\partial l}{\partial o_i} = \text{softmax}(\mathbf{o})_i - y_i = \hat{y}_i - y_i
$$
常见损失函数
L2 Loss
$$
l(y, y’) = \frac{1}{2}(y - y’)^2
$$
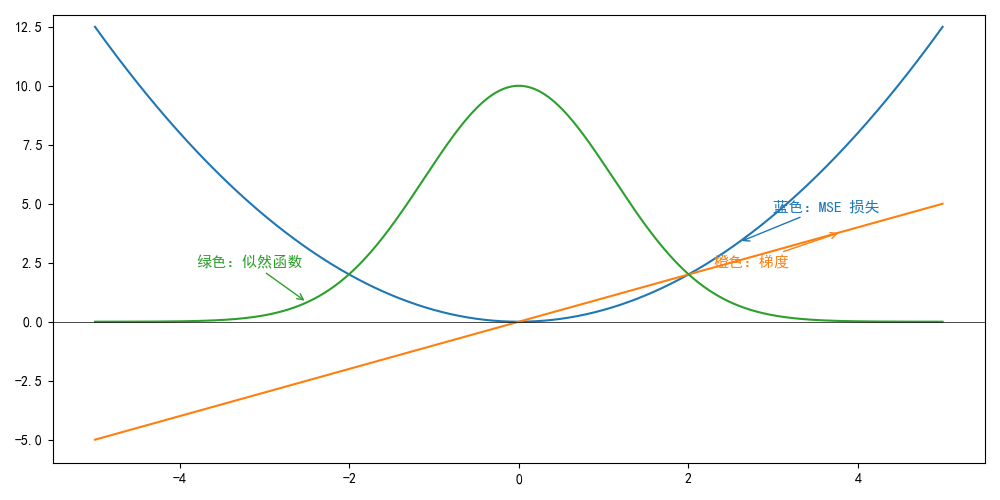
最小化 MSE(平方),你在预测“平均值”(Mean)。此处不再证明推导。俺数学也不好T_T
均方损失MSE的数学解释
基础假设:世界是有“噪声”的。现实中的数据从来不是完美的直线。真实数据$y$等于理想的预测值$\mathbf{w}^\top \mathbf{x} + b$加上一个”噪声”$\epsilon$
$$
y = \mathbf{w}^\top \mathbf{x} + b + \epsilon
$$
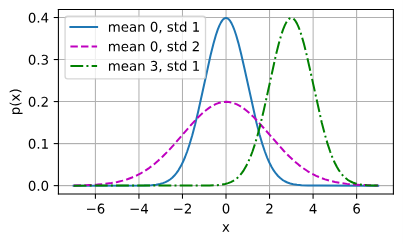
均方损失MSE中,我们假设这个噪声是服从正态分布(高斯分布)的。正太分布概率密度函数如下:
$$
p(z) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{1}{2\sigma^2}(z - \mu)^2 \right).
$$
- $z$ :随机变量的具体取值。
- $\mu$ :这个分布的 均值 (也就是钟形曲线最高点对应的中心位置)。
- $(z - \mu)$ :表示“当前值”距离“中心”有多远。
概率密度函数用于描述连续性随机变量的分布情况。
对于离散变量(比如掷骰子),我们可以说“掷出 6 的概率是 1/6”;但对于连续变量(比如一个人的精确身高),由于取值有无限种可能, 取到某一个精确数值(如刚好 175.0000…cm)的概率在数学上是 0 。
概率密度本身不是概率,但它在某个区间上的积分才是概率。如果你想知道随机变量 $X$ 落在区间 $[a, b]$ 内的概率,只需要对 PDF 求积分。
函数图像一般如下:
现在回到线性回归的公式:
$$
y = \mathbf{w}^\top \mathbf{x} + b + \epsilon
$$
其中噪声 $\epsilon \sim \mathcal{N}(0, \sigma^2)$。
- $\mathbf{w}^\top \mathbf{x} + b$ 是一个 确定值 (一旦 $\mathbf{x}$ 给定,预测出的直线上的点就是固定的)。
- $\epsilon$ 是一个 随机波动 (它是以 0 为中心的)。
如果你把一个“固定值”加上一个“以 0 为中心的随机波动”,得到的结果 $y$ 会是什么分布?
答案是:$y$ 也会服从正态分布,只是中心变了。
- $y$ 的均值(中心 $\mu$) = $\mathbf{w}^\top \mathbf{x} + b$ (也就是预测值)。
- $y$ 的方差(宽窄 $\sigma^2$) = 噪声的方差 $\sigma^2$。
所以,我们可以得出结论:
$$
y \sim \mathcal{N}(\mathbf{w}^\top \mathbf{x} + b, ,, \sigma^2)
$$
因此我们可以写出通过给定的$x$观测到特定的$y$似然 (likelihood):
$$
P(y \mid \mathbf{x}) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{1}{2\sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2 \right).
$$
接下来,在线性归回预测中,我们通常要找到模型参数($w$ 和 $b$),让这堆点出现在这条线周围的“可能性”最大。在数学上,我们将这一过程称为极大似然估计。
极大似然估计:既然我们已经看到了这一组数据($x$ 和 $y$),那么我们要找的那个模型参数($w$ 和 $b$),应该是让这组数据出现的概率最大的那个。
逻辑:寻找一个参数,使得实验结果出现的可能性(似然度)达到最大。
似然函数$L(\theta)$:
$$
L(\theta) = P(x_1, x_2, …, x_n | \theta) = \prod_{i=1}^{n} P(x_i | \theta)
$$
于是我们需要找到$w$ 和 $b$的最优值是使整个数据集的似然函数最大的值:
$$
P(\mathbf{y} \mid \mathbf{X}) = \prod_{i=1}^{n} p(y^{(i)} \mid \mathbf{x}^{(i)}).
$$
为了计算这个“最大概率”,推导过程做了一系列数学变形:
- 连乘变连加: 因为所有样本的概率是要乘起来的,乘法很难算,所以科学家取了对数(log),把乘法变成了加法。
- 最大变最小: 我们原本想让概率(似然) 最大化 。但是数学上通常习惯求 最小值 (比如损失函数)。所以,给公式加了个负号,把“求最大”变成了“求最小负对数似然”。
为了计算这个“最大概率”,推导过程做了一系列数学变形:
- 连乘变连加: 因为所有样本的概率是要乘起来的,乘法很难算,所以科学家取了对数(log),把乘法变成了加法。
- 最大变最小: 我们原本想让概率(似然) 最大化 。但是数学上通常习惯求 最小值 (比如损失函数)。所以,给公式加了个负号,把“求最大”变成了“求最小负对数似然”。
因此可以得到数学公式:
$$
-\log P(\mathbf{y} \mid \mathbf{X}) = \sum_{i=1}^{n} \frac{1}{2} \log(2\pi\sigma^2) + \frac{1}{2\sigma^2} \left( y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b \right)^2.
$$
现在我们只需要假设$\sigma$是某个固定常数就可以忽略第一项, 因为第一项不依赖于和。 现在第二项除了常数外,其余部分和前面介绍的均方误差是一样的。 幸运的是,上面式子的解并不依赖于。 因此,在高斯噪声的假设下,最小化均方误差等价于对线性模型的极大似然估计。
L1 Loss
$$
l(y, y’) = |y - y’|
$$
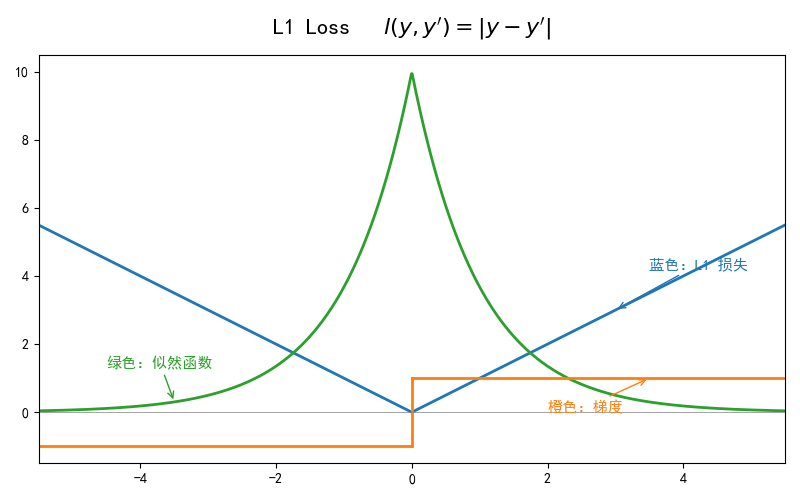
L1 Loss:最小化 MAE(绝对值),你在预测“中位数”(Median)。
Huber’s Robust Loss
$$
l(y, y’) = \begin{cases} |y - y’| - \frac{1}{2} & \text{if } |y - y’| > 1 \ \frac{1}{2}(y - y’)^2 & \text{otherwise} \end{cases}
$$
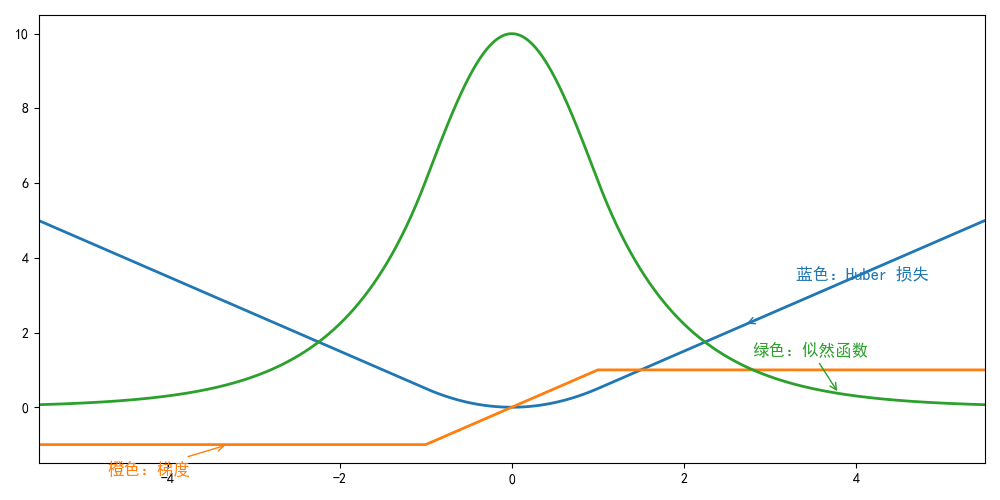
图像分类数据集
这里介绍Fashion-MNIST数据集,作为我们后续softmax回归而使用的数据集。
Fashion-MNIST 数据集 :
- 包含 10 类服装图像(如恤、裤子、裙子等)。
- 每张图像是 $28 \times 28$ 像素的灰度图。
- 训练集共有 60,000 个样本,测试集共有 10,000 个样本。
读取数据集
1 | |
transforms.ToTensor():不仅改变数据类型,还进行了归一化处理。$$
\text{Pixel}{\text{new}} = \frac{\text{Pixel}{\text{old}}}{255}
$$归一化:它的目的是将不同量纲(单位)或取值范围的数据,转换到同一个特定的区间内(通常是 $[0, 1]$ 或 $[-1, 1]$)。
- 加速模型收敛
- 防止大数吃小数,特征权重的平衡
- 避免数值计算问题
我们来看一下Tensor的形状:

数据集由灰度图像组成,其通道数为1。
图像的通道:图像中某一类信息的独立数据层。你可以把一张图像想象成由多个透明的“图层”叠加而成,每个图层记录一种特定的信息,例如红色、绿色、蓝色、透明度等。
灰度图(1通道):
- 只有一个通道,记录亮度。
- 每个像素一个值:0(黑) ~ 255(白)
RGB图像(3通道):
- R 红
- G 绿
- B 蓝
读取小批量
我们使用内置的 data.DataLoader()读取数据。
1 | |
遍历一遍数据的时间:
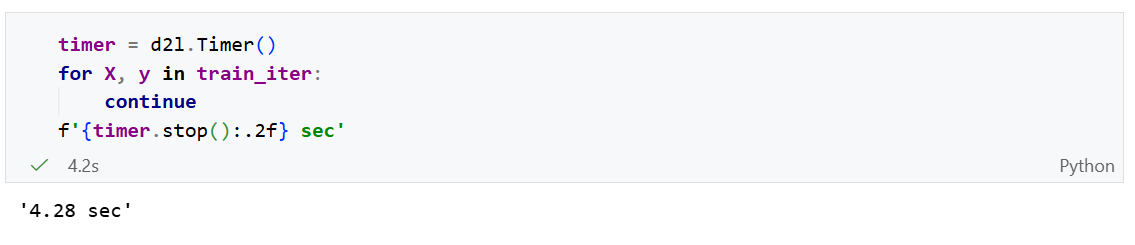
遍历一遍数据的时间为4.28秒。
有时,读取训练数据会成为训练瓶颈。一般要求数据读取速度大于训练速度。
我们可以汇总上述代码,写出一个完整的数据导入函数:
1 | |
softmax回归的从零开始实现
首先导入包以及数据集:
1 | |
初始化参数模型
和之前线性回归的例子一样,这里的每个样本都将用固定长度的向量表示。原始数据集中的每个样本都是28 * 28 的图像。 本节将展平每个图像,把它们看作长度为784(28的平方)的向量。
在softmax回归中:
- 输出与类别一样多,即有10个类别
- 输入维度为784
因此,权重将构成一个$784 \times 10$的矩阵,偏置将构成一个$1 \times 10$的行向量。与线性回归一样,我们将使用正态分布初始化我们的权重W,偏置b初始化为0。
1 | |
定义softmax操作
softmax表达式:
$$
\operatorname{softmax}(\mathbf{X}){i j}=\frac{\exp \left(\mathbf{X}{i j}\right)}{\sum_{k} \exp \left(\mathbf{X}_{i k}\right)}.
$$
步骤:
- 对每个项求幂
- 对每一行求和(小批量中每一行是一个样本),得到每个样本的规范化常数。
- 将每一行除以其规范化常数,确保结果的和为1。
1 | |
定义模型
定义softmax操作后,我们可以实现softmax回归模型。下面的代码定义了输入如何通过网络映射到输出。
1 | |
将数据传递到模型之前,我们使用reshape函数将每张原始图像展平为向量。
定义损失函数
回归问题的损失函数使用:交叉熵损失函数。
$$
l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{i} y_i \log \hat{y}_i = - \log \hat{y}_y
$$
假设我们有一个数据样本y_hat,其中包含2个样本在3个类别的预测概率,以及它们对应的标签y。
1 | |
有了y,我们知道在第一个样本中,第一类是正确的预测;而在第二个样本中,第三类是正确的预测。
接下来我们要获取每个样本中对于正确预测的概率,我们可以使用for,循环,
1 | |
高级索引
然而for循环往往是低效的,我们可以使用高级索引,直接得到:
1 | |
这种写法别称为整数数组索引,它是高级索引中的一种。
- 核心逻辑:提供每一维度的索引列表,来精确”挑出”张量中的特定元素。
确定行索引号:使用第一个列表[0,1]
确定列索引号:使用的是第二个列表y,即 [0.2]
一一对应配对:
- 第一对坐标:
(行索引[0], 列索引[0])$\rightarrow$(0, 0) - 第二对坐标:
(行索引[1], 列索引[1])$\rightarrow$(1, 2)
最后,它会从 y_hat 中取出这些坐标的值,并组成一个新的张量:[y_hat[0, 0], y_hat[1, 2]]
现在,我们只需一行代码集合实现交叉熵损失函数:
1 | |
分类精度
给定预测分布y_hat,当我们必须输出硬预测时,我们通常选择预测概率最高的类。
如Gmail必须将电子邮件分类为
- “Primary(主要邮件)”
- “Social(社交邮件)”
- “Updates(更新邮件)”
- “Forums(论坛邮件)”。
Gmail做分类时可能在内部估计概率,但最终它必须在类中选择一个。当预测与标签分类y一致时,即是正确的。
分类精度即正确预测数量与总预测数量之比。虽然直接优化精度可能很困难(因为精度的计算不可导),但是精度通常是我们最关心的性能衡量标准,我们在训练分类器时几乎总会关注它。
1 | |
然后我们计算得到分类精度:
1 | |
同样,对于任意数据迭代器 data_iter可访问的数据集, 我们可以评估在任意模型 net的精度。
1 | |
其中Accumulator为一个自定义累加器,用于对多个变量进行累加。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Accumulator: #@save
"""在n个变量上累加"""
def __init__(self, n):
# 初始化一个包含 n 个浮点数的列表,全部设为 0.0
# 每个位置对应一个你想要追踪的指标(如:损失、正确数、总样本数)
self.data = [0.0] * n
def add(self, *args):
# 接收任意数量的参数,并将它们分别加到对应的 self.data 插槽中
# 例如:metric.add(a, b) 会执行 self.data[0] += a, self.data[1] += b
self.data = [a + float(b) for a, b in zip(self.data, args)]
def reset(self):
# 重置所有累加器为 0.0
self.data = [0.0] * len(self.data)
def __getitem__(self, idx):
# 允许通过索引访问累加的数据,例如 metric[0]
return self.data[idx]
训练
首先我们定义一个训练函数来代表一个迭代周期:
1 | |
其中updater函数与线性回归中的实现一致:
2
3lr = 0.1
def updater(batch_size):
return d2l.sgd([W, b], lr, batch_size)
然后我们可以实现一个训练函数:
1 | |
Animator:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Animator: #@save
"""在动画中绘制数据"""
def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
ylim=None, xscale='linear', yscale='linear',
fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
figsize=(3.5, 2.5)):
# 增量地绘制多条线
if legend is None:
legend = []
d2l.use_svg_display()
self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
if nrows * ncols == 1:
self.axes = [self.axes, ]
# 使用lambda函数捕获参数
self.config_axes = lambda: d2l.set_axes(
self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
self.X, self.Y, self.fmts = None, None, fmts
def add(self, x, y):
# 向图表中添加多个数据点
if not hasattr(y, "__len__"):
y = [y]
n = len(y)
if not hasattr(x, "__len__"):
x = [x] * n
if not self.X:
self.X = [[] for _ in range(n)]
if not self.Y:
self.Y = [[] for _ in range(n)]
for i, (a, b) in enumerate(zip(x, y)):
if a is not None and b is not None:
self.X[i].append(a)
self.Y[i].append(b)
self.axes[0].cla()
for x, y, fmt in zip(self.X, self.Y, self.fmts):
self.axes[0].plot(x, y, fmt)
self.config_axes()
display.display(self.fig)
display.clear_output(wait=True)
现在我们可以进行10轮的训练:
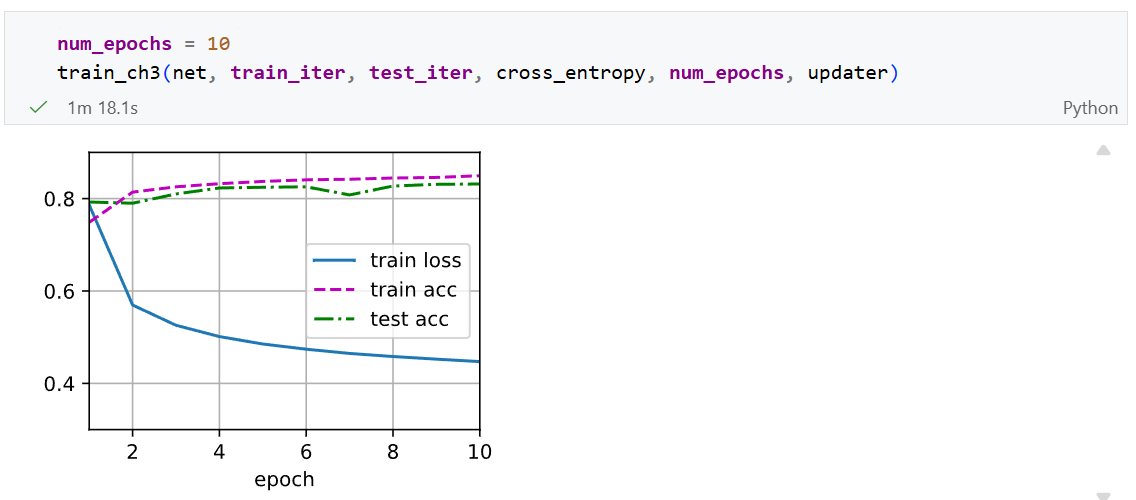
预测
现在训练已经完成,我们的模型已经准备好对图像进行分类预测。 给定一系列图像,我们将比较它们的实际标签(文本输出的第一行)和模型预测(文本输出的第二行)。

softmax的简洁实现
通过深度学习框架的高级API也能更方便地实现softmax回归模型。
首先导入包与数据:
1 | |
初始化模型参数
softmax回归的输出是一个全连接层。因此,为了实现我们的模型,我们只需在Sequential中添加一个带有10给输出的的全连接层。
全连接层:前一层的所有神经元,都与当前层的所有神经元相连。
数学上的表达:
对于全连接层,每一个输出 $y_j$ 都是所有输入 $x_i$ 的线性组合。如果有 $d$ 个输入和 $q$ 个输出,其计算公式为:
$$
y_j = \sum_{i=1}^{d} x_i w_{ij} + b_j
$$
1 | |
softmax的实现
直接计算softmax函数:
$$
\hat{y}_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)}
$$
上溢风险
如果输入的某个$o_k$很大,$\exp(o_k)$会爆炸,变成 inf无穷大,导致无法计算。这种情况下我们无法得到一个明确定义的交叉熵值。
解决技巧:减去最大值
为了防止exp爆炸,在计算指数前,先让所有的$o_k$减去它们中的最大值$\max(o_k)$:
$$
\hat{y}_j = \frac{\exp(o_j - \max(o_k))}{\sum_k \exp(o_k - \max(o_k))}
$$
这样最大的指数就变成了 $\exp(0) = 1$,所有的值都缩放到 $(0, 1]$ 之间,彻底解决了上溢问题。
下溢风险
在减去和规范化步骤之后,可能有些$o_j - max(o_k)$具有较大的负值。由于精度受限$exp(o_j - max(o_k))$将有接近0的值,即下溢。这些值可能会四舍五入为0。使得$\hat{y}_j = 0$,并使$\log(0)$ = -inf
。反向传播几步后,我们可能会发现自己面对一屏幕可怕的 nan结果。
解决技巧:Log-Sum-Exp技巧
尽管我们要计算指数函数,但我们最终在计算交叉熵损失时会取它们的对数。通过将softmax和交叉熵结合在一起,可以避免反向传播过程中可能会困扰我们的数值稳定性问题。
$$
\begin{aligned}
\log \left(\hat{y}{j}\right) & =\log \left(\frac{\exp \left(o{j}-\max \left(o_{k}\right)\right)}{\sum_{k} \exp \left(o_{k}-\max \left(o_{k}\right)\right)}\right) \
& =\log \left(\exp \left(o_{j}-\max \left(o_{k}\right)\right)\right)-\log \left(\sum_{k} \exp \left(o_{k}-\max \left(o_{k}\right)\right)\right) \
& =o_{j}-\max \left(o_{k}\right)-\log \left(\sum_{k} \exp \left(o_{k}-\max \left(o_{k}\right)\right)\right).
\end{aligned}
$$
如上面的等式所示,我们避免计算$\exp (o_{j}-\max (o_{k}))$,而也可以直接使$o_{j} - \max(o_{k})$,因为$\log(\exp(\cdot))$被抵消了。
1 | |
当我们使用PyTorch的 CrossEntropyLoss时,我们的模型最后一层不应该再加Softmax激活函数。我们应该直接把未规范化的预测值传递给损失函数,因为内部它会帮我们高效且稳定地完成图片里说的这些复杂计算。
优化算法
在这里,我们使用学习率为0.1的小批量随机梯度下降作为优化算法。 这与我们在线性回归例子中的相同,这说明了优化器的普适性。
1 | |
训练函数
1 | |
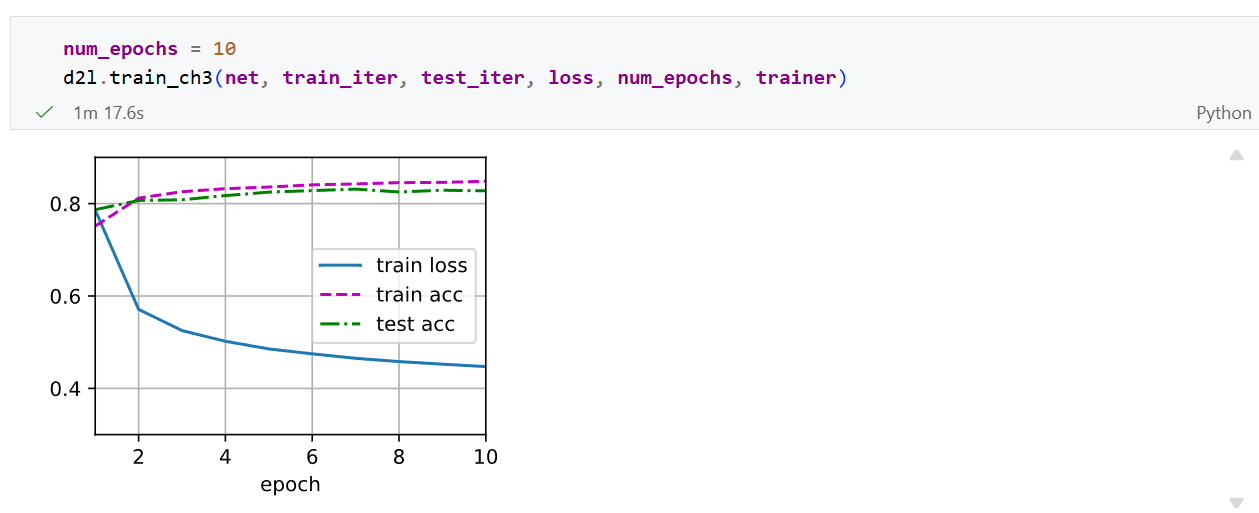
bug
在最后的softmax回归的简洁实现中,遇到错误:
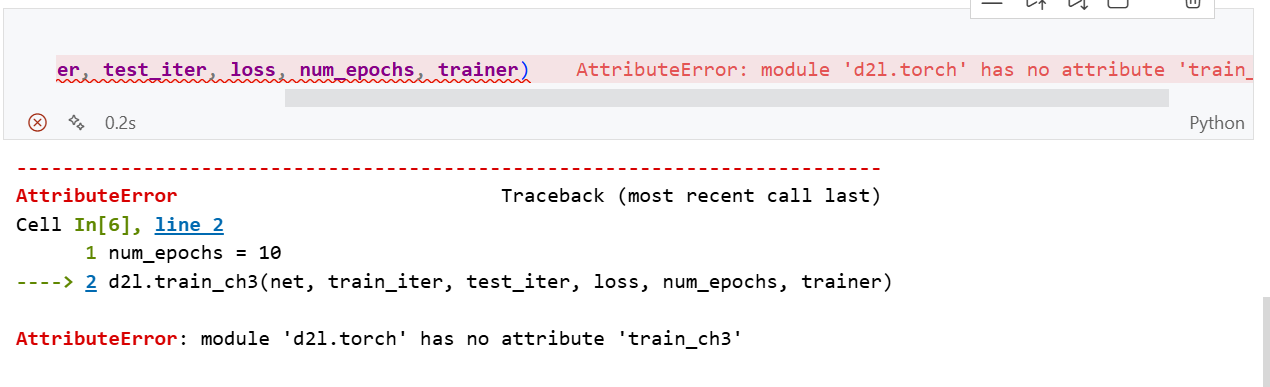
修复:
按住ctrl然后点击d2l,进入d2l.torch包中,在包中添加以下代码:
1 | |