2026 新年快乐！

本blog参考李沐老师的动手学习深度学习，使用pytorch框架

安装环境

安装pytorch：

1

pip install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu121

1

pip install d2l==1.0.3

坑死我了，书上安装的版本为 0.17.6，存在依赖地狱。

数据操作

N维数组

N维数组是机器学习和神经网络的主要数据结构：

分类：

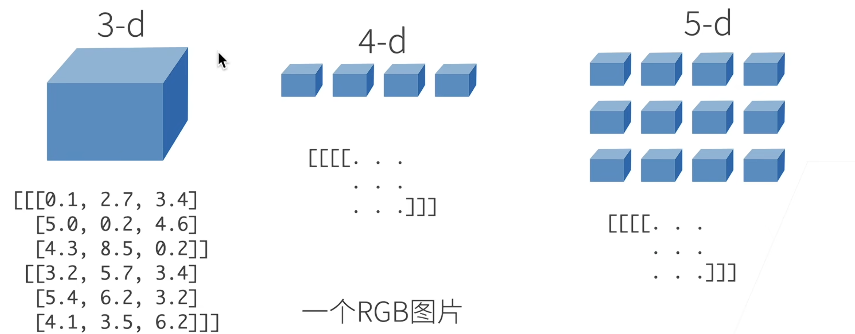
• 0-d(标量)：一个类别
• 1-d(向量)：一个特征向量
• 2-d(矩阵)：一个样本——特征矩阵

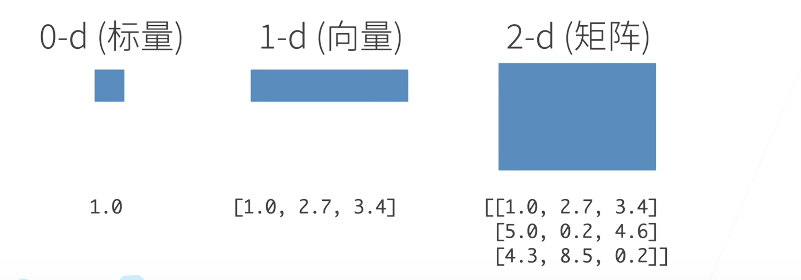
• 3-d：RGB图片(长x宽x颜色)
• 4-d：一个RGB图片批量(批量大小x长x宽x颜色)
• 5-d：一个视频批量。(批量大小x时间x长x宽x颜色)

创建张量

创建数组需要：

• 形状：例如3x4
• 每个元素的数据类型：例如32位浮点数
• 每个元素的值：例如全是0，或者随机数

在机器学习中，n维数组也称为张量(tenser)。

创建一维张量

1
2
3
4

import torch

//创建行向量
x = torch.arange(12)

arange创建一个行向量x。这个行向量包含以0开始的前12个整数，它们默认创建为整数，但是也可以指定创建类型为浮点数。torch.arange(12, dtype=torch.float32)

创建多维向量

以形状为(2,3,4)的张量为例：

创建全0张量：torch.zeros()

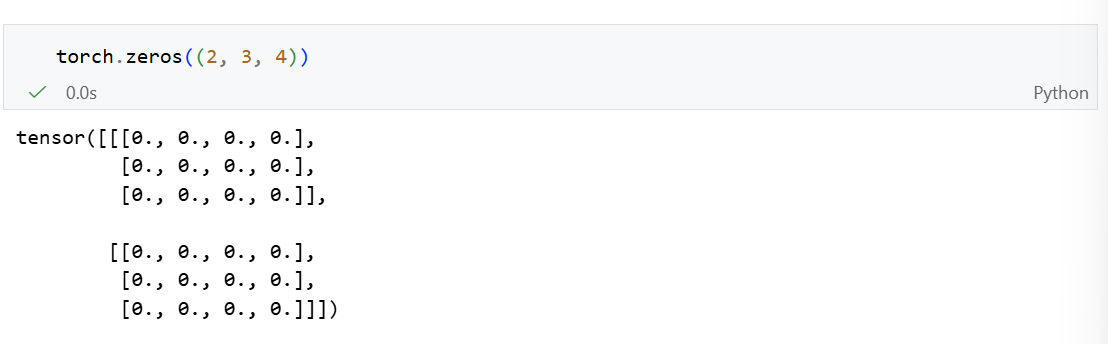
创建全1张量：torch.ones()

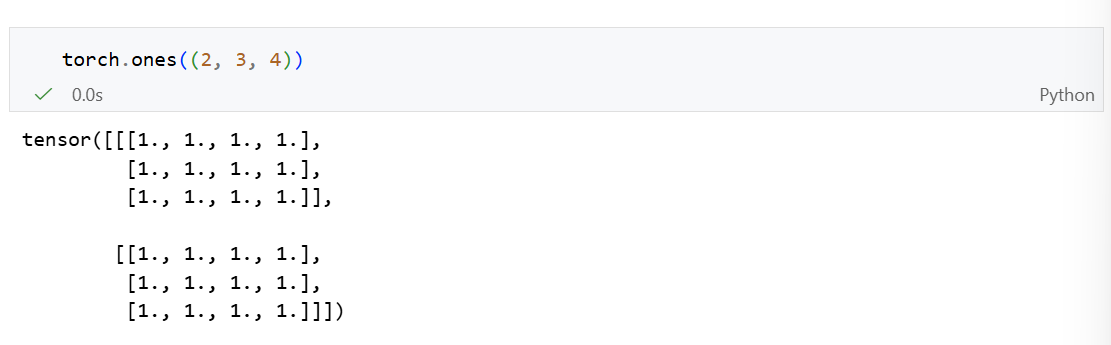
常用：随机初始化参数值：torch.randn()

每个元素都从均值为0、标准差为1的标准高斯分布(正太分布)中随机采样。

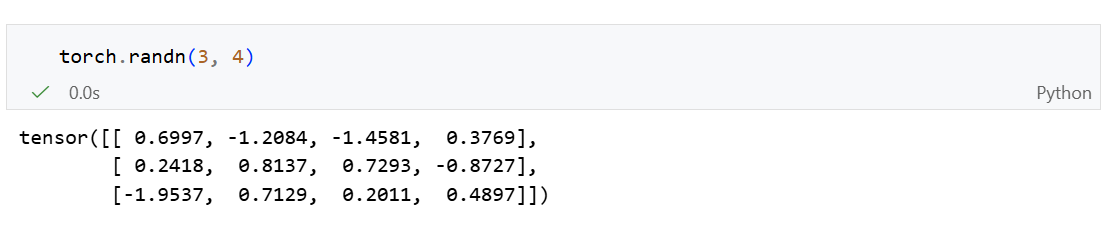
基于python列表创建：torch.tensor()

复制张量

我们可以通过 clone()来在在内存中复制一份独立的对象。

1

B = A.clone()	# 通过分配新内存，将A的一个副本分配给B

访问张量属性

访问张量的形状：

shape属性可以访问张量(沿每个轴的长度)的形状。

访问张量的元素总数：

修改张量的形状

想要改变一个张量的形状而不改变元素数量和元素值，可以使用 reshape函数。

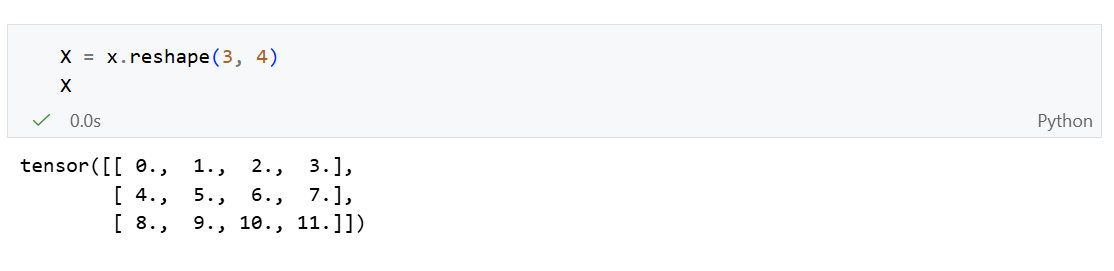
或者使用-1，自动计算维度：

1
2

X = x.reshape(-1, 4)
X = x.reshape(3, -1)

reshape与view的区别

View

view()也是一个修改张量形状的方法。

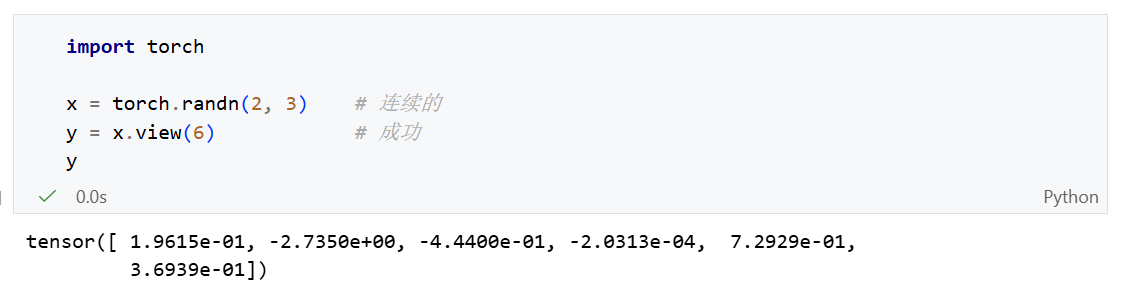
view的核心是内存共享。它不会产生数据拷贝，只是改变了观察数据的方式。

• 限制条件：张量必须是连续的
• 连续性是什么：在内存中，张量的元素是按顺序一个接一个存储的。如果你对张量进行了 transpose（转置）或 permute（维度交换），内存里的物理顺序没变，但逻辑顺序变了，这时候张量就不再连续。

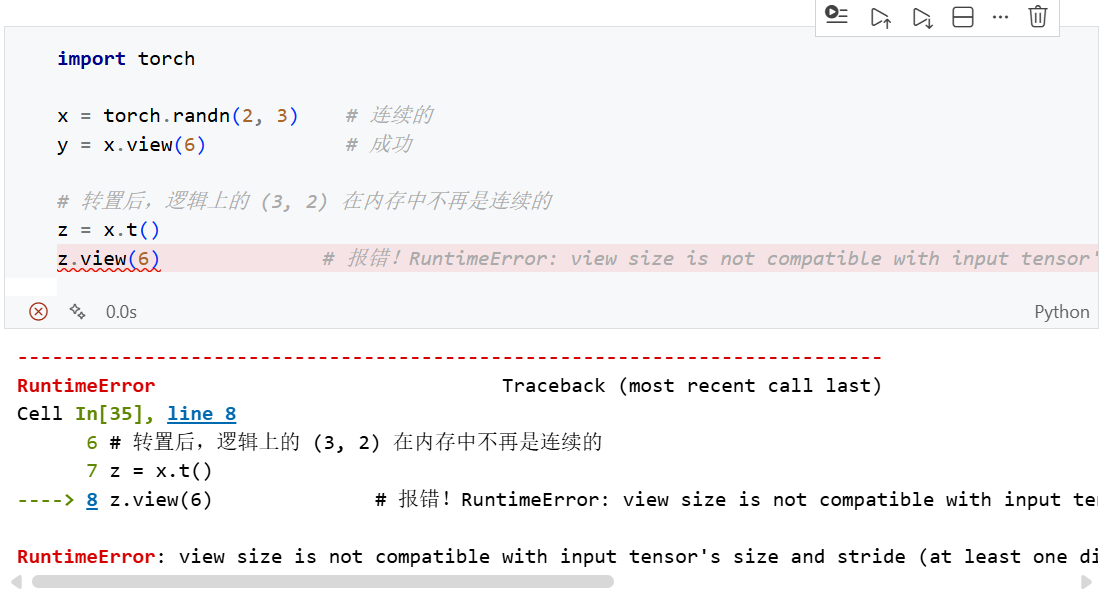
所以view()返回张量其实是共享地址的，不可轻易修改一个张量的数据，物理地址相同的其他张量数据也会收到影响。

reshape 更智能，更鲁棒

reshape会自动判断张量是否连续，并使用不同的方法进行处理：

1. 如果张量是连续的，就像 view一样工作，返回共享内存的视图。
2. 如果张量是非连续的，会自动调用 .contiguous()将数据拷贝到一段新的连续内存中，然后再改变形状。

使用 reshpe()后，可能涉及数据拷贝，有时候你可能没有意识到自己增加了额外的内存开销。

运算符

按元素计算

对于任意有相同形状的张量，常见的标准算术运算符，(+, -, *, /和 ** )都可以被升级为按元素运算。我们可以在同一形状的任意两个张量上调用按元素操作。

张量x中所有数据都将被提升为浮点数类型。

求幂运算

1

torch.exp(x)

逻辑运算符

通过逻辑运算符可以构建二元张量：

线性代数运算

连结运算

我们可以把多个张量连结在一起成为一个更大的张量：

其中dim为连结的维度。

• dim=0，沿行连结
• dim=1，沿列连结

当连结一个维度时，其他维度必须要相等。即：

• 当dim=0，沿行连结时，X、Y两个张量的列数必须要相等
• 当dim=1，沿列连结时，X、Y两个张量的行数必须要相等

求和运算(降维)

对张量中的所有元素进行求和，会产生一个单元素张量。

我们还可以通过指定张量沿哪一个轴来求和(降维)。

广播机制

在某些情况下，即使形状不同，我们仍然可以通过调用 广播机制 （broadcasting mechanism）来执行按元素操作。

这种机制的工作方式如下：

1. 通过适当复制元素来扩展一个或两个数组，以便在转换之后，两个张量具有相同的形状；
2. 对生成的数组执行按元素操作。

工作条件入下：

1. 其中一个维度为 1 ：此时该维度会被“拉伸”以匹配另一个张量。
2. 其中一个维度不存在 ：如果一个张量的维数少于另一个，则在较短张量的形状左侧补 1。

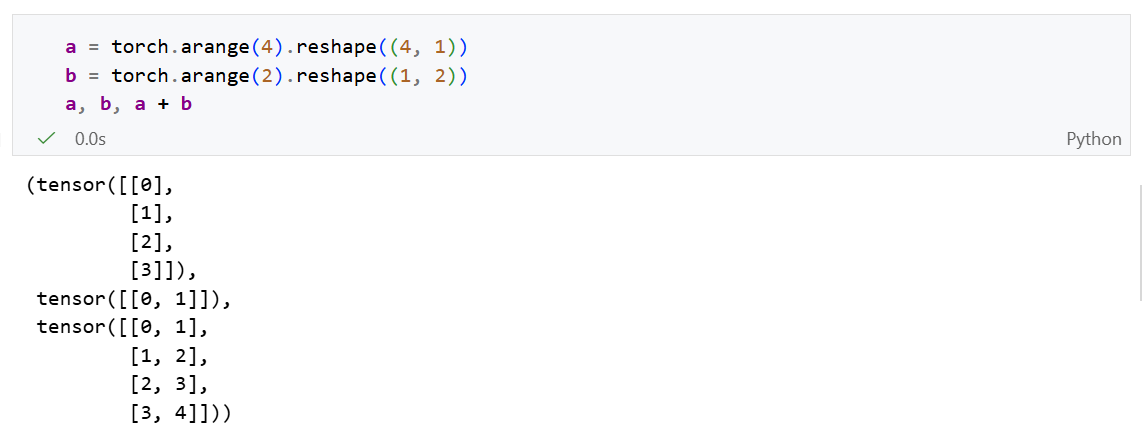
索引和切片

可以使用 X[-1]来访问最后一行，使用 X[1:3]选择下标为 [1,3)的所有行：

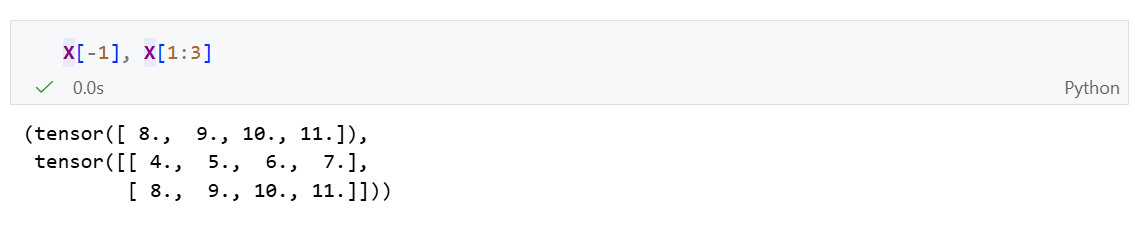
用逗号 ,分割表示下一维度：

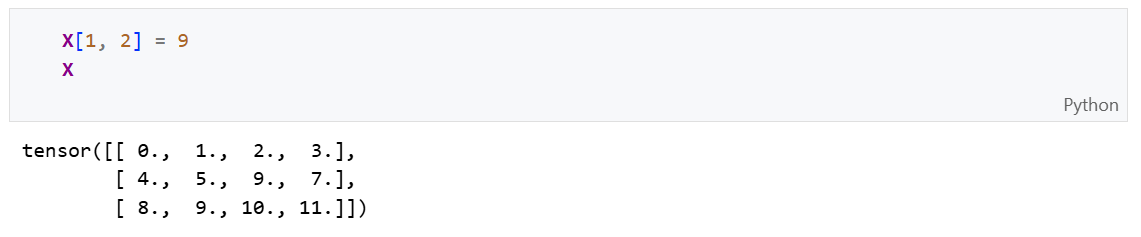
如果想为多个元素批量赋值，只需要索引所有元素，然后为它们赋值：

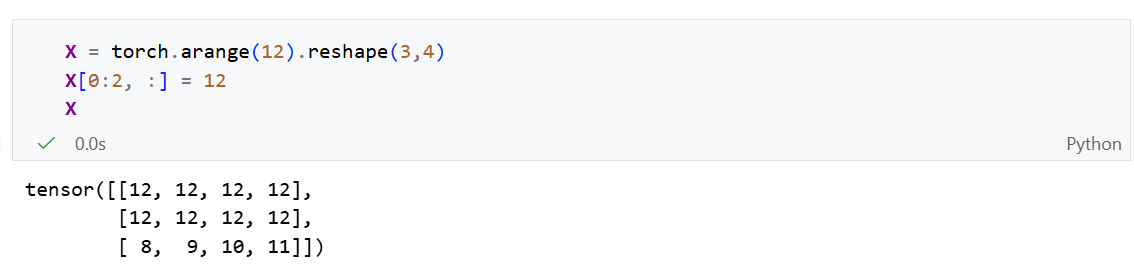
节省内存

运行一些操作可能导致为新结果分配内存。如：

id()会返回一个对象在python中的唯一标识符。标识符一样则内存地址一样，标识符改变则占用了一块新的内存空间。

这可能是不可取的，原因有两个：

1. 首先，我们不想总是不必要地分配内存。在机器学习中，我们可能有数百兆的参数，并且在一秒内多次更新所有参数。通常情况下，我们希望原地执行这些更新；
2. 如果我们不原地更新，其他引用仍然会指向旧的内存位置，这样我们的某些代码可能会无意中引用旧的参数。

执行原地复制操作：

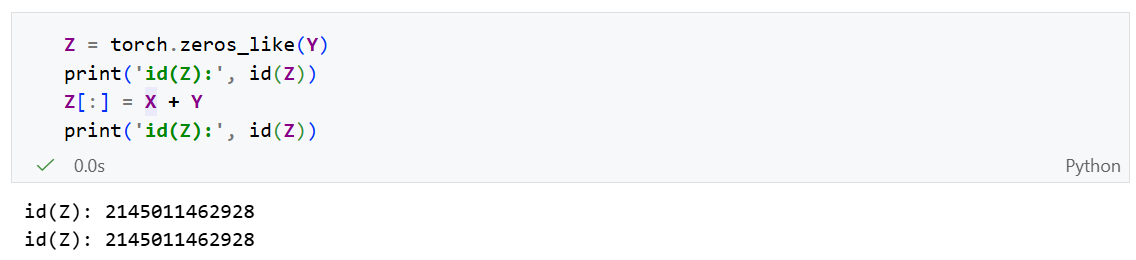
通过在赋值时切片，即可不改变对象Z的地址，而是让Z的每一个元素等于对应的计算结果。

转换为其他Python框架

转换为numpy张量，再转回torch张量：

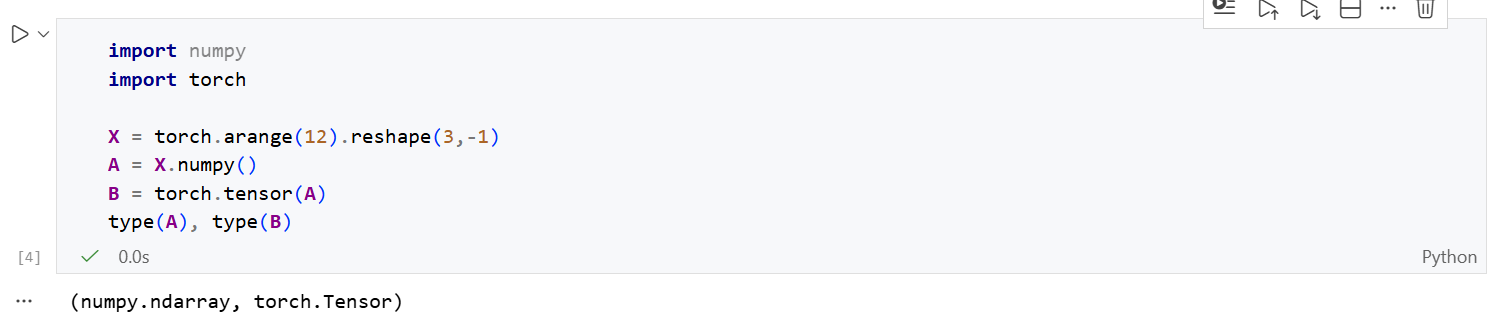
此处踩坑：如果环境以及安装numpy但是遇到报错：numpy is not avaliable。可能是numpy版本过高>=2.0所导致。

解决方法：

1	conda install "numpy<2.0"

然后重启Jupyter Notebook 的内核即可。

将大小为1的张量转换为python标量：

数据预处理

以一个简单的csv文件为例：../data/house_tiny.csv

1
2
3
4
5

NumRooms,Alley,Price
NA,Pave,127500
2,NA,106000
4,NA,178100
NA,NA,140000

加载数据

要从csv中加载原始数据集，我们导入pandas库，并调用 read_csv()。

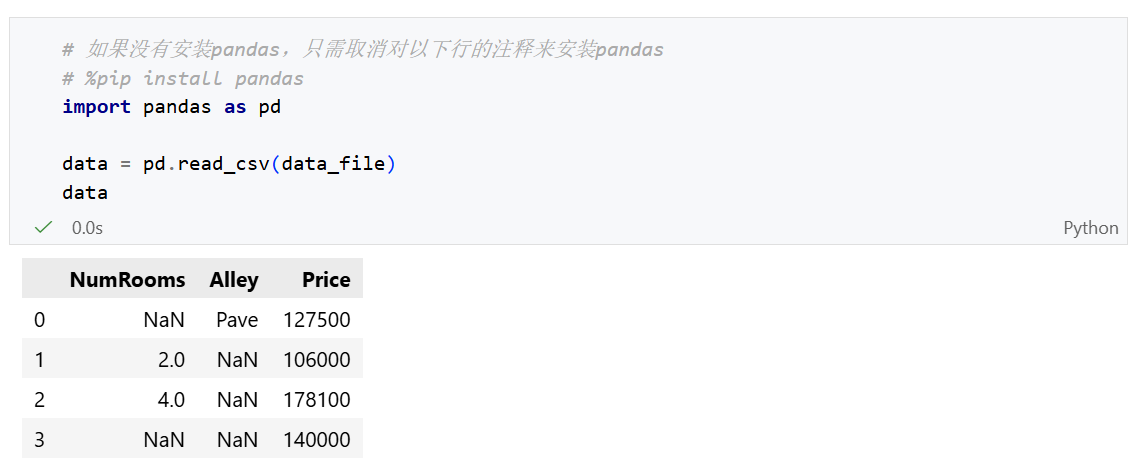
NaN(Not a Number)：代表缺失值。

处理缺失值

为了处理缺失值，典型的方法包括插值法和删除法。

• 插值法：用一个值代替弥补缺失值。
• 删除法：直接忽略缺失值。

这里我们演示插值法：

通过位置索引iloc，我们将数据集分为输入集input(NumRooms、Alley)以及输出集output(Price)。

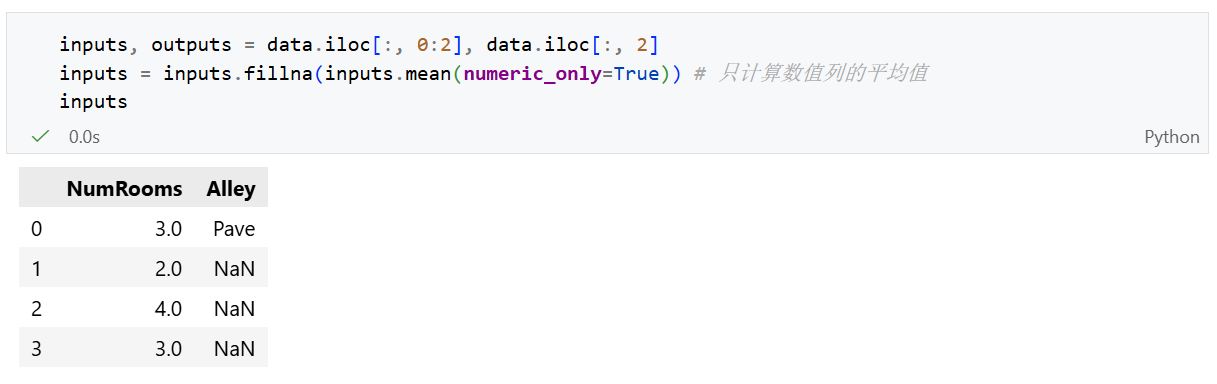
当像如上进行切片操作时，iloc会创建一个view返回，这意味这它们是共享内存的。

对于Alley中的离散值，或类别值，我们将NaN视为一个类别。转化为两列：Alley_Pave和 Alley_nan。再用0和1表示是否拥有这一项。pandas可以自动帮我们实现这一转换：

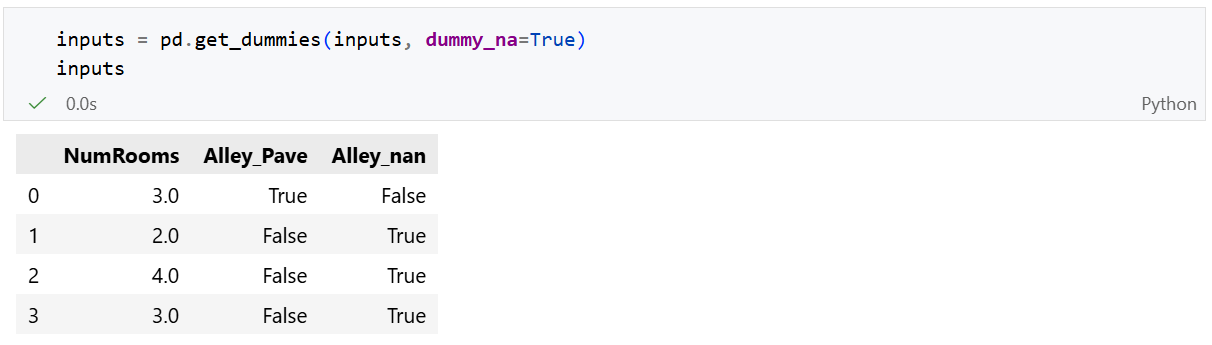
转换为张量

现在所有的input和output中的所有条目都是数值类型，它们可以转换为张量格式。

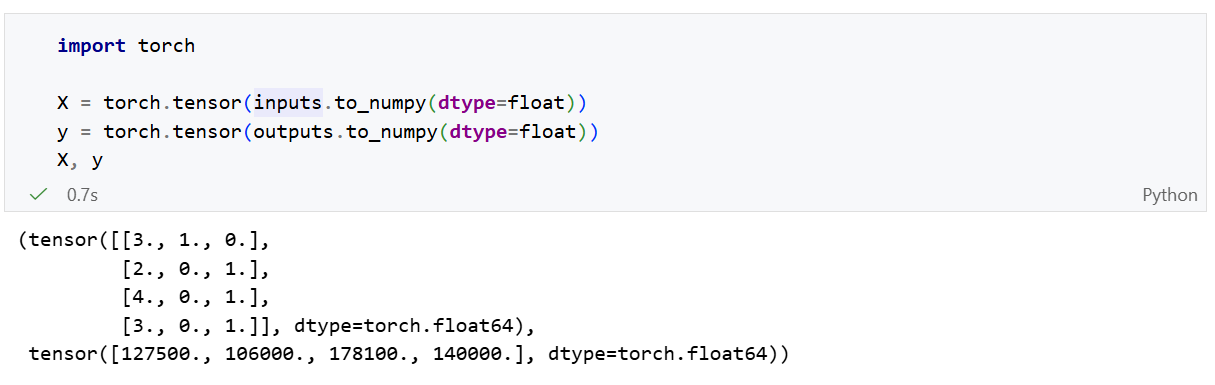
线性代数

多维数组是一个计算机中的概念，张量则是数学中的概念。

概念理解

范数

如果你把向量看作空间中的一个点，向量的范数就是它到原点的“距离”；那么对于矩阵，范数就是衡量这个矩阵作为“数据集合”或“线性变换”时的强度或 规模 。

$$
c = A \cdot b \quad \text{hence} \quad |c| \le |A| \cdot |b|
$$

矩阵范数：最小的满足上面公式的值。

矩阵的Frobenius范数：

$$
|A|{\text{Frob}} = \left[ \sum{ij} A_{ij}^2 \right]^{\frac{1}{2}}
$$

将整个矩阵拉成一条向量，然后求向量的范数。

特殊矩阵

对称矩阵

$$
A_{ij} = A_{ji}
$$

反对称矩阵

$$
A_{ij} = -A{ji}
$$

正交矩阵

如果一个 $n \times n$ 的实方阵 $Q$ 满足以下条件，则称其为正交矩阵：

$$
Q^T Q = Q Q^T = I
$$

其中 $Q^T$ 是 $Q$ 的转置矩阵，$I$ 是单位矩阵。

这个定义暗示了一个核心特性：正交矩阵的逆矩阵等于它的转置矩阵。

$$
Q^{-1} = Q^T
$$

置换矩阵

置换矩阵是一种非常直观且重要的特殊方阵。简单来说，它就是将单位矩阵 $I$ 的行（或列）进行重新排列后得到的矩阵。

一个 $n \times n$ 的矩阵 $P$ 被称为置换矩阵，当且仅当：

• 矩阵的每一行有且仅有一个 $1$，其余元素全为 $0$。
• 矩阵的每一列有且仅有一个 $1$，其余元素全为 $0$。

例子

一个 $3 \times 3$ 的置换矩阵可能长这样（它是单位矩阵交换第 1 行和第 2 行的结果）：

$$
P = \begin{bmatrix} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & 1 \end{bmatrix}
$$

作用：

A. 对矩阵进行行/列交换

• 左乘 ($PA$) ：相当于对矩阵 $A$ 进行 行交换 。
• 右乘 ($AP$) ：相当于对矩阵 $A$ 进行 列交换 。

B. 对向量进行重排

如果向量 $v = [v_1, v_2, v_3]^T$，左乘上面提到的那个矩阵 $P$：

$$
\begin{bmatrix} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} v_1 \ v_2 \ v_3 \end{bmatrix} = \begin{bmatrix} v_2 \ v_1 \ v_3 \end{bmatrix}
$$

可以看到，$v_1$ 和 $v_2$ 的位置互换了。

特征向量

特征向量（Eigenvector） 是矩阵在线性变换过程中“不改变方向”的那些特殊向量。

在数学上，如果一个非零向量 $v$ 与方阵 $A$ 相乘的结果，仅仅是该向量在原方向上缩放了 $\lambda$ 倍，那么 $v$ 就是 $A$ 的特征向量，而 $\lambda$ 就是对应的 特征值（Eigenvalue） 。

核心公式：

$$
Av = \lambda v
$$

• A：一个 $n \times n$ 的方阵（代表一种线性变换，如旋转、拉伸）。
• $v$ ：特征向量（变换后方向保持不变的向量）。
• $\lambda$ ：特征值（缩放的比例）。如果 $\lambda > 1$ 是拉伸，$\lambda < 1$ 是压缩，$\lambda < 0$ 则表示反向。

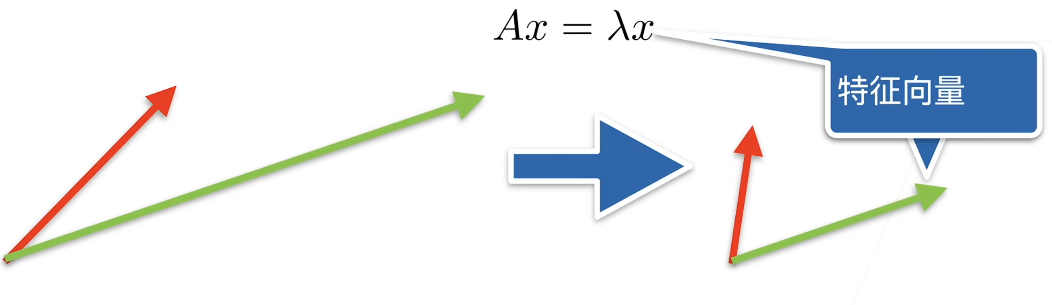
绿色的向量在矩阵乘法后，没有改变方向，即为矩阵A的一个特征向量。

代码实现

标量

只有一个元素的张量表示。

标量的运算就是我们熟悉的数字运算：

向量

标量值组成的列表。这些标量值被称为向量的元素、分量。

矩阵

矩阵将向量从一阶推广到二阶。在代码中表示有两个轴的张量。

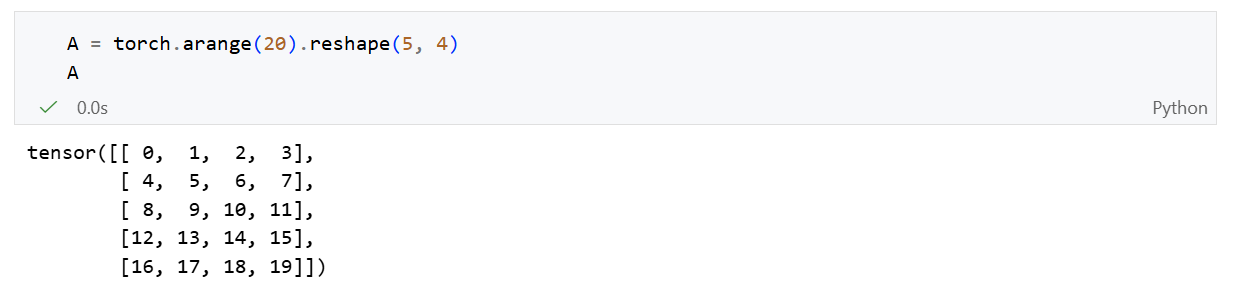
矩阵的转置

张量

张量是矩阵的推广，描述具有任意数量轴的n维数组的通用方法。

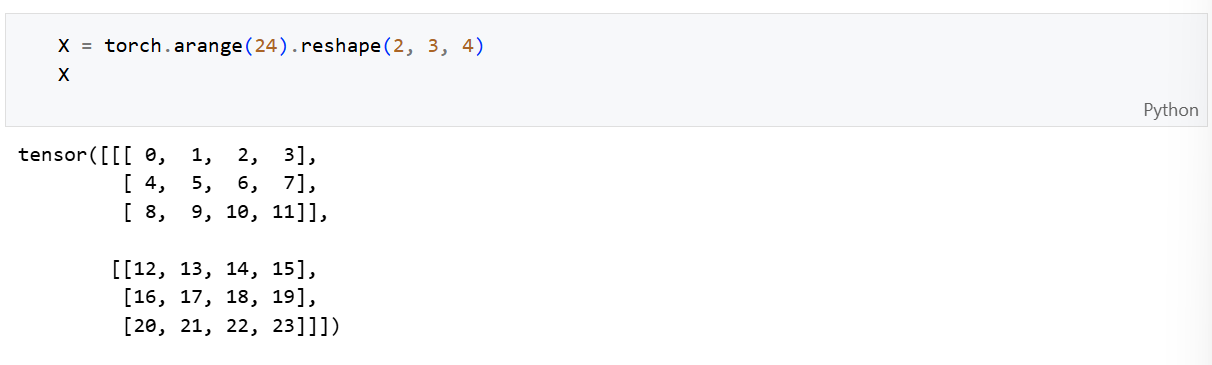
降维

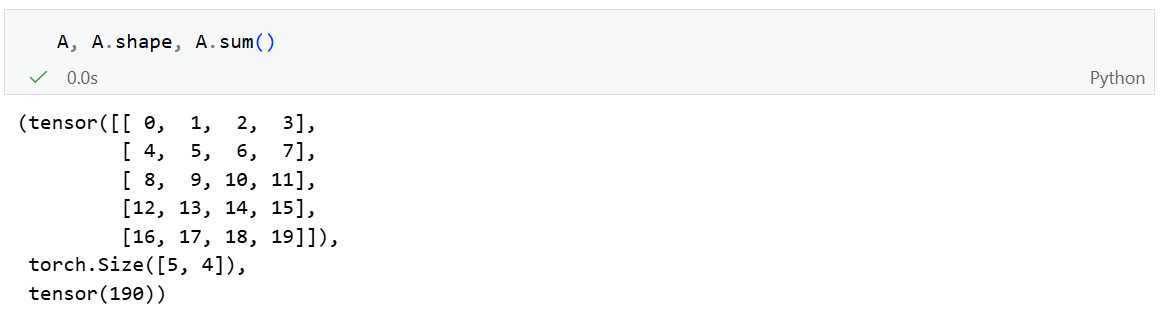
默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。但是我们还可以指定张量沿哪一个轴来通过求和降低维度。

以矩阵为例：

• 沿0轴降维：
  

• 沿1轴降维：

  

• 同时沿两个轴降维：

  

  对于矩阵来说，同时沿两个轴降维后变为标量。

平均值(mean)

计算所有元素的平均值：

计算指定维度的平均值：

非降维求和

如果我们直接使用 sum(axis = 1)降维后，矩阵变为向量，直接减少了一个维度。如果我们接下来需要使用广播机制，就不希望维度减少，而是希望维度值变为1。我们可以指定 keepdims=True。

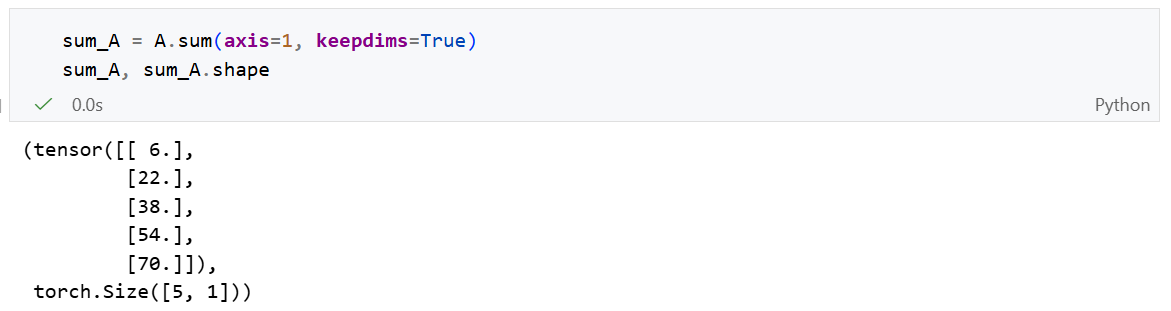
由于sum_A在对每行进行求和后仍然保持两个维度，我们可以使用广播将A除以sum_A。

如果我们想沿某个轴计算 A元素的累积总和， 比如 axis=0，可以调用 cumsum()函数。 此函数不会沿任何轴降低输入张量的维度。

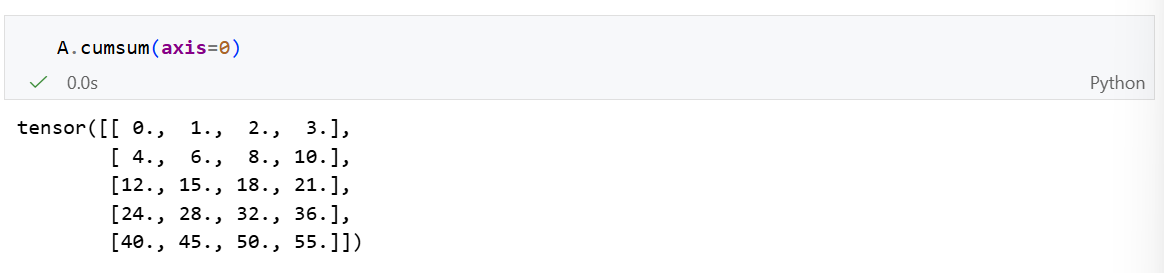
点积

给定两个 $d$ 维向量 $\mathbf{x}, \mathbf{y} \in \mathbb{R}^d$，它们的点积 $\mathbf{x}^\top \mathbf{y}$（或 $\langle \mathbf{x}, \mathbf{y} \rangle$）定义为对应位置元素的 乘积之和 ：

$$
\mathbf{x}^\top \mathbf{y} = \sum_{i=1}^d x_i y_i = x_1 y_1 + x_2 y_2 + \dots + x_d y_d
$$

矩阵-向量积（matrix-vector product）

计算矩阵 $\mathbf{A}$ 与向量 $\mathbf{x}$ 的乘积最直观的方法是 行点积（Row Dot Product） ：

步骤 ：将矩阵 $\mathbf{A}$ 看作是由多个行向量 $\mathbf{a}_i^\top$ 堆叠而成的。

计算 ：结果向量的第 $i$ 个元素，就是矩阵 $\mathbf{A}$ 的第 $i$ 行与向量 $\mathbf{x}$ 的 点积 （Dot Product）。

公式：

$$
\mathbf{A}\mathbf{x} = \begin{bmatrix} \mathbf{a}_1^\top \ \mathbf{a}_2^\top \ \vdots \ \mathbf{a}_m^\top \end{bmatrix} \mathbf{x} = \begin{bmatrix} \mathbf{a}_1^\top \mathbf{x} \ \mathbf{a}_2^\top \mathbf{x} \ \vdots \ \mathbf{a}_m^\top \mathbf{x} \end{bmatrix}
$$

其中每一项 $\mathbf{a}_i^\top \mathbf{x}$ 都是按照点积方式计算的标量。

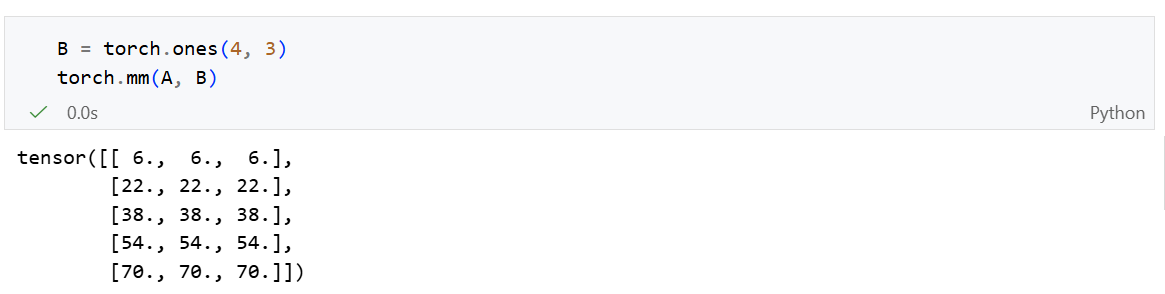
矩阵-矩阵乘法

矩阵乘法 $\mathbf{C} = \mathbf{AB}$ 实际上可以看作是多次点积运算的集合：

• 结果矩阵 $\mathbf{C}$ 中的每一个元素 $c_{ij}$，都是由左矩阵 $\mathbf{A}$ 的第 $i$ 行与右矩阵 $\mathbf{B}$ 的第 $j$ 列进行点积得到的。
• 数学公式：

$$
c_{ij} = \mathbf{a}i^\top \mathbf{b}j = \sum{l=1}^k a{il} b_{lj}
$$

其中 $\mathbf{a}_i^\top$ 是 $\mathbf{A}$ 的行向量，$\mathbf{b}_j$ 是 $\mathbf{B}$ 的列向量。

范数

向量范数

计算L2范数：

$$
|\mathbf{x}|2 = \sqrt{\sum{i=1}^n x_i^2}
$$

使用 torch.norm()

计算L1范数：

$$
|\mathbf{x}|1 = \sum{i=1}^n |x_i|.
$$

矩阵范数

矩阵最常计算Frobenius范数：

$$
|\mathbf{X}|F = \sqrt{\sum{i=1}^m \sum_{j=1}^n x_{ij}^2}.
$$

矩阵计算

亚导数

亚导数是导数概念在不可微的凸函数上的推广。

简单来说，一个凸函数在某一点不可导（比如存在“尖角”）时 molding，我们无法定义切线，但可以定义一系列“支撑线”，这些线的斜率集合就是亚导数。

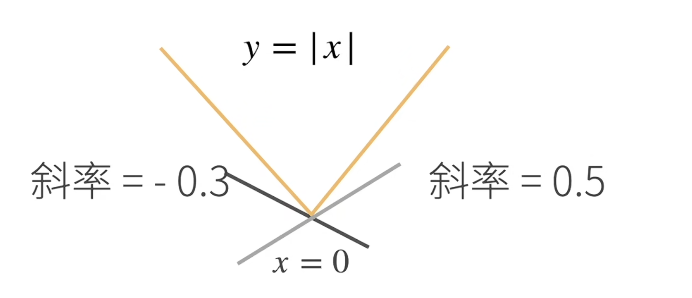
y = |x| 的亚导数定义为：

$$
\frac{\partial |x|}{\partial x} = \begin{cases}
1 & \text{if } x > 0 \
-1 & \text{if } x < 0 \
a & \text{if } x = 0, \quad a \in [-1, 1]
\end{cases}
$$

y = max(x, 0)的亚导数定义为：

$$
\frac{\partial}{\partial x} \max(x,0) = \begin{cases}
1 & \text{if } x > 0 \
0 & \text{if } x < 0 \
a & \text{if } x = 0, \quad a \in [0, 1]
\end{cases}
$$

将导数拓展到向量(梯度)

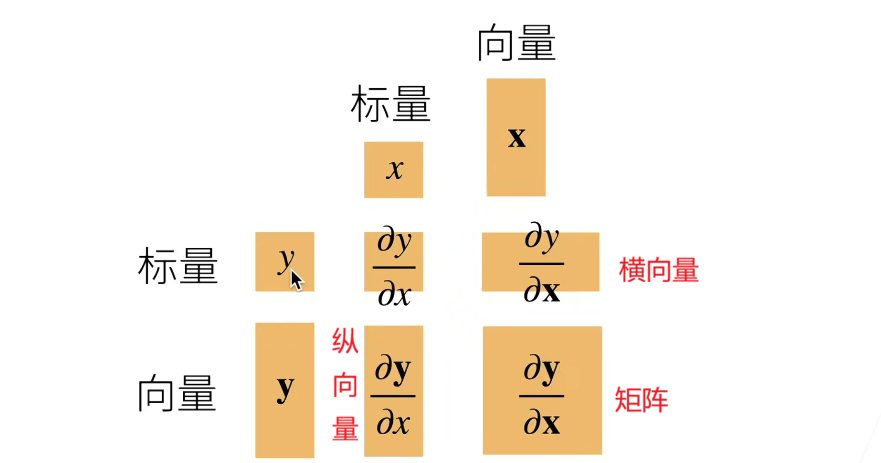
这个版本被称之为分子布局符号。

y标量、x为列向量

$$
\mathbf{x} = \begin{bmatrix}
x_1 \
x_2 \
\vdots \
x_n
\end{bmatrix} \quad
\frac{\partial y}{\partial \mathbf{x}} = \left[ \frac{\partial y}{\partial x_1}, \frac{\partial y}{\partial x_2}, \dots, \frac{\partial y}{\partial x_n} \right]
$$

例子：$\frac{\partial}{\partial \mathbf{x}} x_1^2 + 2x_2^2 = [2x_1, 4x_2]$

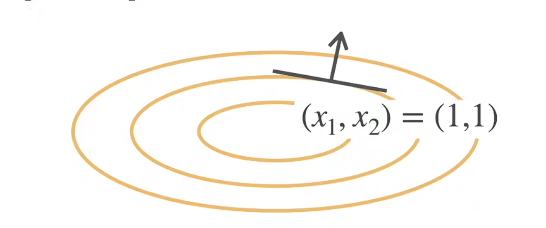
梯度是与函数图像的等高线相切，代表变化最大的方向。

y列向量、x为标量

$$
\mathbf{y} = \begin{bmatrix}
y_1 \
y_2 \
\vdots \
y_m
\end{bmatrix} \quad
\frac{\partial \mathbf{y}}{\partial x} = \begin{bmatrix}
\frac{\partial y_1}{\partial x} \
\frac{\partial y_2}{\partial x} \
\vdots \
\frac{\partial y_m}{\partial x}
\end{bmatrix}
$$

y、x都为列向量

$$
\mathbf{x} = \begin{bmatrix}
x_1 \
x_2 \
\vdots \
x_n
\end{bmatrix}, \quad
\mathbf{y} = \begin{bmatrix}
y_1 \
y_2 \
\vdots \
y_m
\end{bmatrix}
$$

每个元素y关于向量x的导数为一个横向量，最终变为一个矩阵：

$$
\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \begin{bmatrix}
\frac{\partial y_1}{\partial \mathbf{x}} \
\frac{\partial y_2}{\partial \mathbf{x}} \
\vdots \
\frac{\partial y_m}{\partial \mathbf{x}}
\end{bmatrix} = \begin{bmatrix}
\frac{\partial y_1}{\partial x_1}, \frac{\partial y_1}{\partial x_2}, \dots, \frac{\partial y_1}{\partial x_n} \
\frac{\partial y_2}{\partial x_1}, \frac{\partial y_2}{\partial x_2}, \dots, \frac{\partial y_2}{\partial x_n} \
\vdots \
\frac{\partial y_m}{\partial x_1}, \frac{\partial y_m}{\partial x_2}, \dots, \frac{\partial y_m}{\partial x_n}
\end{bmatrix}
$$

链式法则

标量链式法则：

$$
y = f(u), \quad u = g(x) \quad
\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u} \frac{\partial u}{\partial x}
$$

拓展到向量：

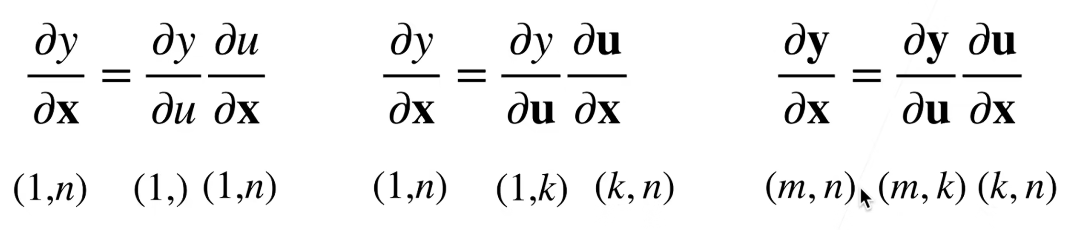
自动求导

自动求导计算一个函数在指定值上的导数。

计算图

步骤：

• 将代码分解为操作子。
• 将计算表示成一个无环图。

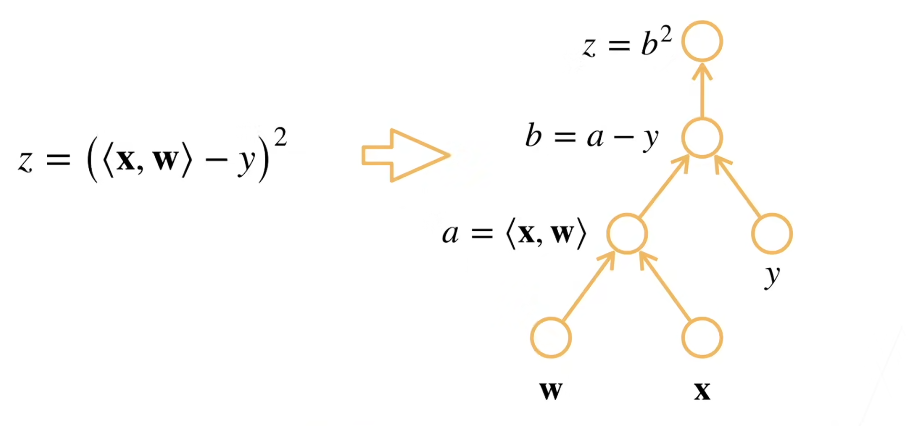
计算图的构造有两种方式：

• 显示构造：
  • 框架：Tensorflow/Theano/MXNet
• 隐式构造：
  • 框架：PyTorch/MXNet

自动求导的两种模式

前置概念：

• 前向传播：沿计算图输入到输出，计算各节点的函数值。
• 反向传播：沿计算图从输出到输入，基于前向传播中保存的中间结果，应用链式法则，逐层计算输出（通常是 Loss）对各中间变量和参数的梯度。

前向传播 != 正向积累

反向传播 != 反向积累

正向积累

正向积累是从自变量输入开始，顺着计算图的方向，逐层计算中间变量对输入的导数。

公式表达：计算顺序是从右向左结合

$$
\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u_n} \left( \frac{\partial u_n}{\partial u_{n-1}} \left( \dots \left( \frac{\partial u_2}{\partial u_1} \frac{\partial u_1}{\partial x} \right) \right) \right)
$$

计算逻辑：进行前向传播(计算函数值)的同时，计算切向量(导数)。(计算图自底向上计算)

使用场景：当输入维度n远小于输出维度m时效率最高。例如，一个输入变量对应多个输出指标。

缺点：如果有100万个参数(输入)，就需要对每个参数运行一次正向过程，计算开销极大。

反向积累

反向积累是从因变量(输出)开始，逆着计算图的方向，逐层计算输出对中间变量的导数。这正是深度学习中 反向传播 (Backpropagation) 的数学本质。

公式表达：

$$
\frac{\partial y}{\partial x} = \left( \left( \left( \frac{\partial y}{\partial u_n} \frac{\partial u_n}{\partial u_{n-1}} \right) \dots \right) \frac{\partial u_2}{\partial u_1} \right) \frac{\partial u_1}{\partial x}
$$

计算逻辑：

1. 前向传播：计算loss，记录所有的中间结果(激活值)
2. 反向传播：从最后的误差开始，应用链式法则回传梯度,更新参数。

使用场景：当输出维度m远小于输入维度n时效率最高。

• 在深度学习中，Loss通常是一个标量(m=1)，而权重参数w有数百万个。
• 反向积累只需要一次反向运行，就能算出Loss对所有参数的梯度。

缺点：需要存储前向传播的所有中间激活值，内存开销极大。

Loss即为损失/误差。

自动求导代码实现

标量自动求导

假设我们需要对函数$y = 2\mathbf{x}^\top\mathbf{x}$关于列向量x求导

首先我们创建变量x并为其分配一个初始值：

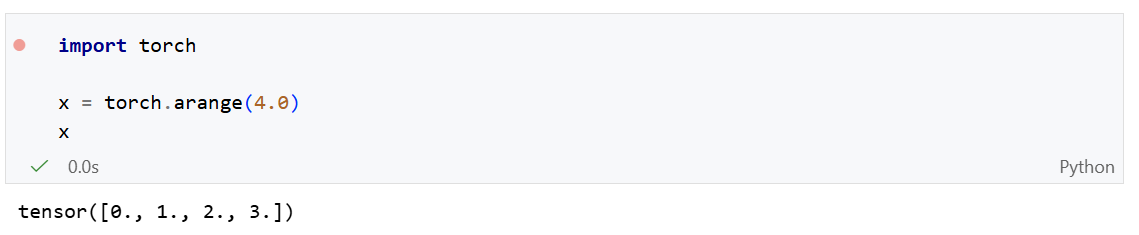
在我们计算梯度之前，我们需要一个地方来存储梯度。所以我们需要显示告诉框架：

反向积累需要记录所有的中间结果。

现在计算y：

接下来，我们通过调用反向传播函数自动计算y关于x每个分量的梯度：

现在我们计算x的另一个函数：

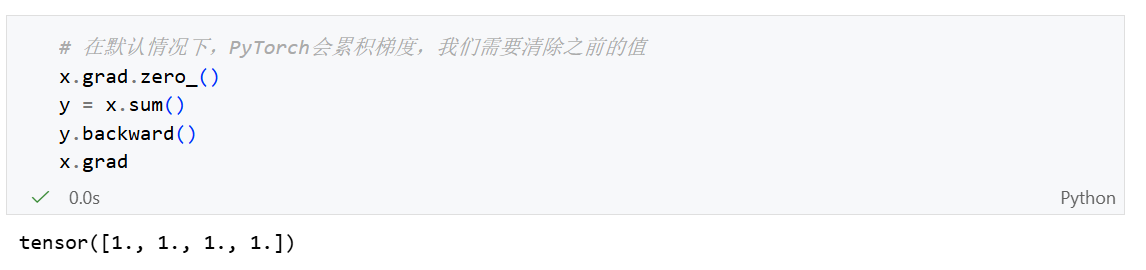
累计梯度演示：如果我们不执行 x.grad.zero_()那么每次一个输出变量(例如 y)执行一次 backward()都会将梯度累加到x当前的grad上。

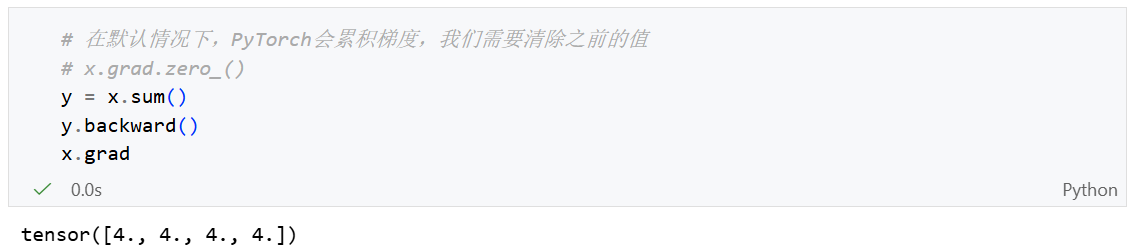
上图为我注释 x.grad.zero_()后又调用三次 backward()后的结果。

非标量变量的反向传播

当y不是标量时，向量y关于向量x的导数的最自然解释是一个矩阵。对于高阶和高维的y和x，求导的结果可以是一个高阶的张量。

虽然这些更奇特的对象确实出现在高级机器学习中（包括深度学习中）， 但当调用向量的反向计算时，我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。 这里，我们的目的不是计算微分矩阵，而是单独计算批量中每个样本的偏导数之和。

个人理解：应该是让一批样本的Loss和最小。

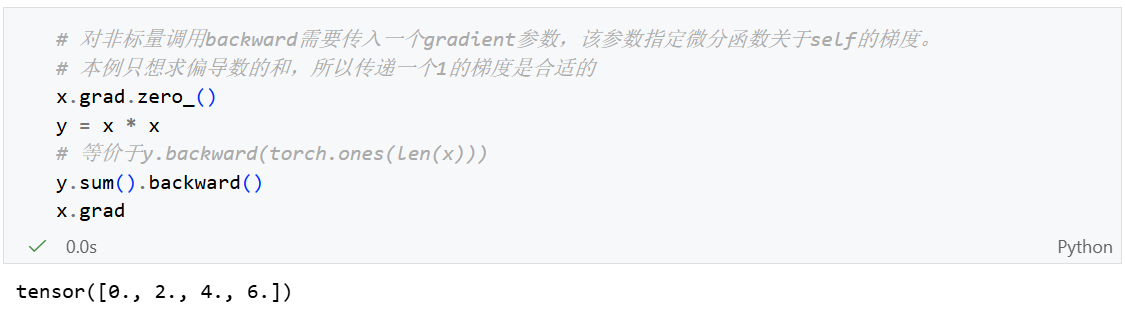
分离计算

有时，我们希望将某些计算移动到记录的计算图之外。

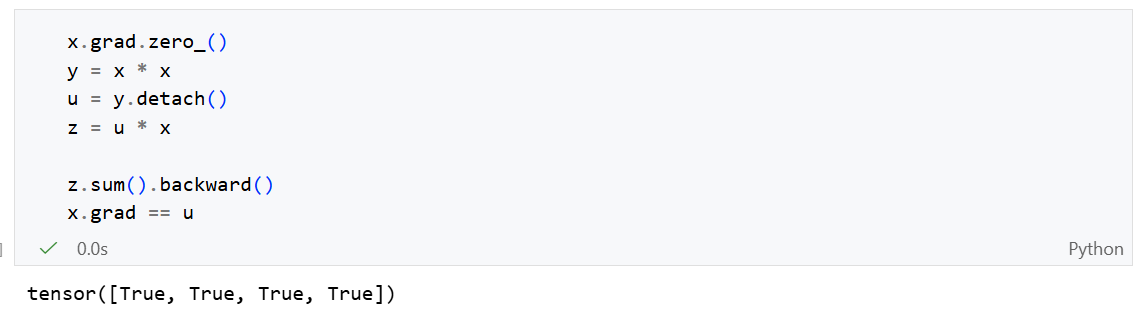
通过 u = y.detach()，我们将u从原本y -> x 的计算图中分离。在调用 z.backward()时梯度不会从u流向x。而是将u当作一个常数，这个常数与y具有相同的值。

Python控制流的梯度计算

使用自动微分的一个好处：即使构建函数的计算图需要通过Python控制流(例如：条件、循环、任意的函数调用)，我们仍然可以计算得到变量的梯度。

假设我们定义了这样一个函数：(包含while， if等)

1
2
3
4
5
6
7
8
9

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

我们仍然可以计算出d关于输入变量a的梯度。