数据结构-图

每日一言

As a sister, and our lovable Iris, violence does not become you. – Maki Oze
from Fire Force

图形结构

基本概念：

• 非线性结构，数据元素之间呈多对多的关系。将数据元素作为顶点，数据元素间的关系作为顶点间的连接，即由顶点集合V和一个描述顶点之间关系——边的集合VR(或E)组成。

图的定义：

$$
Graph = (V,VR) \ 或 \ Graph=(V,E)
$$

• V：顶点（数据元素）的又穷非空集合
• VR（或E）：弧（关系）的又穷集合

相关术语：

• 顶点：数据元素所构成的顶点

• 有向图：弧的顶点偶对是有序的。对于弧$<v_1, v_2>$，$v_1$是弧尾/初始点，$v_2$是弧头/终端点

• 无向图：弧的顶点偶对是无序的。对于弧$(v_1,v_2)$和$(v_2,v_1)$是一条边

• （无向）完全图：每个顶点与其余顶点都有边的无向图。$e = \frac{n(n-1)}{2}$

• 有向完全图：每个顶点与其余顶点都有弧的有向图。$e = n(n-1)$

• 稀疏图：有很少边或弧的图

• 稠密图：有较多边或弧的图

• 权：图中的边或弧具有一定的大小的概念

• 网：边/弧带权的图

• 邻接：有弧相连的两个顶点之间的关系。

• 关联（依附）：与顶点相连的边称为与该顶点关联。

• 顶点的度：与该顶点相关联的边的数目。记为$D(v)$

• 路径：接续的边构成的顶点序列。

  • 路径长度：路径上边的数目/权值之和
  • 回路（环）：第一个顶点与最后一个顶点相同的路径
  • 简单路径：序列中顶点均不相同的路径
  • 简单回路（简单环）：除路径的顶点和终点外，其余点都不相同的路径

• 连通图(强连通)

  • 无向图：任何两个顶点v, 都存在从v到u的路径
  • 有向图（强连通）：任何两个顶点v, 都存在从v到u的路径
  • 有向图（弱连通）：在忽视边的有向性后，满足：任何两个顶点v, 都存在从v到u的路径

• 子图：对于图 $G = (V, E)$ 和 $G’ = (V’, E’)$，如果 $V’ \subseteq V$，$E’ \subseteq E$，且 $E’$ 中的边关联的顶点都在 $V’$ 中，则称 $G’$ 是 $G$ 的子图。

• 生成子图：由图的全部顶点和部分边组成的子图称为原图的生成子图。

• 生成树：包含图中全部顶点的极小连通子图。

• 生成有向树：图中恰有一个顶点入度为0，其余顶点入度均为1

• 生成森林：向图中，包含所有顶点的若干棵有向树构成的子图。

• 连通分量：无向图G 的极大连通子图称为G的连通分量。

  

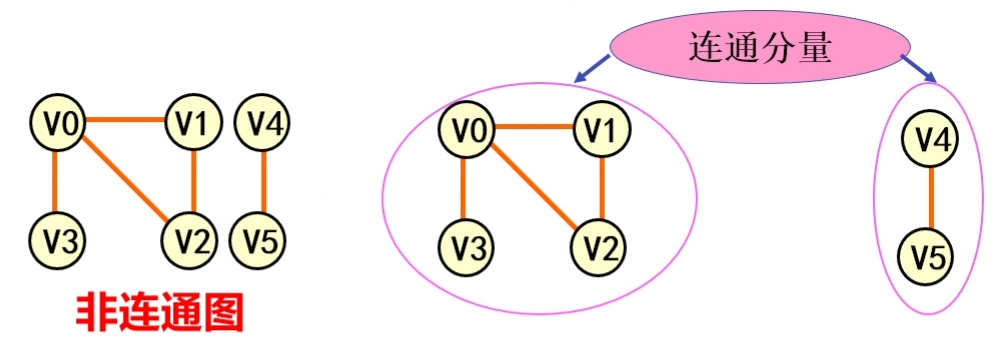
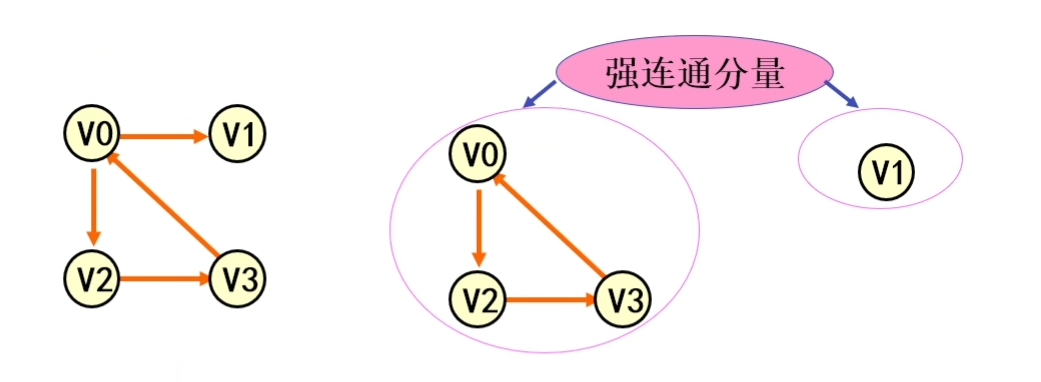
• 强连通分量：有向图G 的极大强连通子图称为G的强连通分量。极大强连通子图意思是：该子图是G的强连通子图，将G的任何不在该子图中的顶点加入，子图不再是强连通的。

  

图的存储结构

顺序存储结构

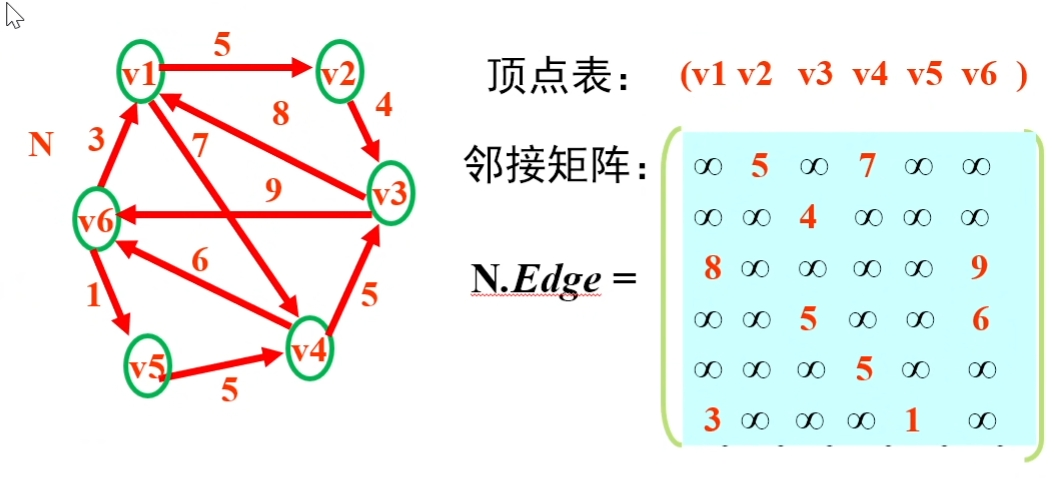
数组表示法（邻接矩阵）：

1. 建立一个顶点表，记录各个顶点信息
2. 建立一个邻接矩阵，表示各个顶点之间的关系

无向图的邻接矩阵表示法

有向图的邻接矩阵表示法

以邻接矩阵的行作为出度边，以邻接矩阵的列作为入度边。

对于顶点$v_i$：

• 出度 = 第I行元素之和
• 入度 = 第i列元素之和
• 度 = 出度 + 入度

网(有权图)的邻接矩阵表示法

将不相连的为止记为$\infty$，相连的位置则记为他们之间的权：

$$
N_Edge[i][j] = \left{
\begin{array}{ll}
W_{ij} & \text{如果} \ (vi, vj) \in VR \
\infty & \text{否则}
\end{array}
\right.
$$

邻接矩阵的存储结构定义

//邻接矩阵
#define MAX_VERTEX_NUM 20   //最大顶点数

typedef enum{DG,DN,UDG,UDN} GraphKind;  //图的类型，有向图、有向网、无向图、无向网
typedef int VertexType;     //顶点的数据类型
typedef int VRType;         //边的数据类型
typedef struct ArcCell {
    VRType adj;             //无权图为0、1,有权图为权重

}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

typedef struct MGraph{      //图的数据结构
    VertexType vexs[MAX_VERTEX_NUM];    //顶点的数组
    AdjMatrix arcs;         //邻接矩阵
    int vexnm,arcnum;       //顶点和边的个数
    GraphKind kind;         //图的类型
}Mgraph;

特点

优点：容易实现图的操作

缺点：存储空间效率低$O(n^2)$

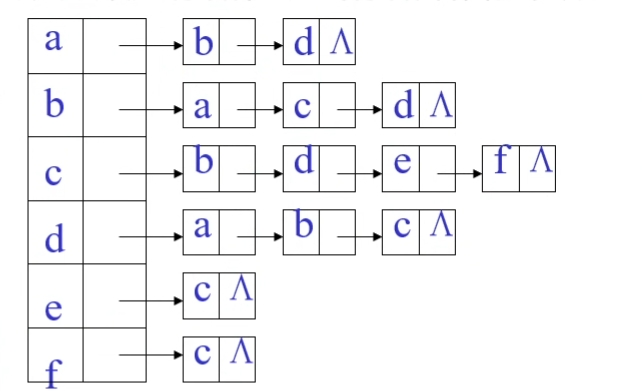
邻接表（链式表示法）

邻接表

邻接表是一种用于表示图的数据结构，它使用一个数组，其中每个元素是一个链表，链表中的每个节点表示与该顶点相邻的顶点。

如图：

空间效率为：$O(n+2e)$

邻接表的链式表示法

对于每个顶点$v_i$建立一个单链表，把与$v_i$有关联的边的信息连接起来。对于网图，结点中还需要保存他们之间边的权值。

存储结构定义

//邻接表的结构定义
#define MAX_VERTEX_NUM 20   //最大顶点数
typedef enum{DG,DN,UDG,UDN} GraphKind;  //四种图的类型
typedef int VertexType;     //顶点携带信息类型

typedef struct ArcNode{     //边结点
    int adjvex;     //该边的另一个顶点
    struct ArcNode *nextarc;    //下一条边的指针
    int weight;     //该边的权重
}ArcNode;

typedef struct VNode {      //顶点结点
    VertexType data;    //顶点存储信息
    ArcNode *firstarc;  //该顶点第一条边的指针
}Vnode,     //顶点结点重命名
AdjList[MAX_VERTEX_NUM];    //定义一个顶点数组

typedef struct{     //图的结构体定义
    AdjList vertices;   //顶点数组
    int vexnum,arcnum;  //顶点数和边数
    GraphKind kind;     //图的类型
}ALGraph;

邻接矩阵与邻接表表示法的关系

1. 联系：邻接表中每个链表对应于邻接矩阵中的一行，但是只储存有邻接的结点，链表中结点个数等于一行中非零元素的个数。
2. 区别：
   1. 对于任一确定的无向图，邻接矩阵是唯一的，但是邻接表不唯一。
   2. 邻接矩阵的空间复杂度为$O(n^2)$，而邻接表的空间复杂度为$O(n+e)$
   3. 邻接表空间效率高，容易寻找顶点的邻接点；
   4. 邻接矩阵空间效率低，但是容易找顶点相关的边或弧；
3. 邻接矩阵多用于稠密图；而邻接表多用于稀疏图

十字链表

十字链表表示稀疏矩阵

十字链表将每个非零元素存储为一个结点，结点由五个数据域组成：

1. row域：存储元素的行号
2. col域：存储元素的列号
3. v域：存储本元素的值
4. right域：指向同行中该元素右边的第一个元素
5. down域：指向同列中下方最近的第一个元素

十字链表将矩阵从行方向和列方向链接起来。

十字链表表示有向图

十字链表的定义

在十字链表中，每个顶点和边都有专门的节点来存储它们的信息。以下是结构的详细定义：

1. 顶点节点 (Vertex Node) :

• data : 存储顶点的数据。
• first_in : 指向以该顶点为终点的第一条边（入边）。
• first_out : 指向以该顶点为起点的第一条边（出边）。

1. 边节点 (Edge Node) :

• tailvex : 该边的起点索引。
• headvex : 该边的终点索引。
• headlink : 指向下一条以相同终点为终点的边（入边链表）。
• taillink : 指向下一条以相同起点为起点的边（出边链表）。
• info : 存储该边的权值或其他附加信息。

邻接多重表

邻接多重表表示无向图

邻接多重表的定义

邻接多重表是一种边节点共享的链表结构，用来表示无向图。每条边只存储一次，并通过两个指针同时链接到其两个关联顶点。以下是邻接多重表的核心组成部分：

1. 顶点节点 (Vertex Node) :

每个顶点由一个节点表示，包含以下字段：

• data : 存储顶点的数据。
• firstedge : 指向该顶点的第一条边。

2. 边节点 (Edge Node) :

每条边由一个节点表示，包含以下字段：

• ivex : 该边关联的一个顶点的索引。
• jvex : 该边关联的另一个顶点的索引。
• ilink : 指向下一个与 ivex 关联的边。
• jlink : 指向下一个与 jvex 关联的边。
• info : 存储该边的权值或附加信息（可选）。

图的遍历

• 遍历定义：从已给的连通图中某一顶点出发，沿着一些边访遍图中所有的顶点，且使每个顶点仅被访问一次，就叫做图的遍历，它是图的基本运算，是求解图的连通性、拓扑排序和求关键路径的基础。
• 遍历实质：找每个顶点的邻接点的过程。
• 图遍历的特点：由于图中可能存在回路，且图的任一顶点都可能与其它顶点相通，在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点，需要在到达曾经访问过的点时回溯，算法实现时要考虑这一点和树的遍历不同的地方。

避免遍历重复访问

设置辅助数组 visited[n] ,用来标记每个被访问过的点。

// 初始化为0
int visited[n] = {0};
//被访问后
visited[i] = 1;

深度优先搜索(DFS)

DFS 的基本思想

1. 从图中的某个顶点出发，将该顶点标记为已访问。
2. 依次访问与该顶点直接相连的未访问顶点，继续递归进行搜索。
3. 如果当前顶点的所有相邻顶点都已被访问，回溯到上一个顶点。
4. 重复上述过程，直到所有顶点都被访问。

伪代码

DFS(v):
    标记 v 为已访问
    输出 v
    对于 v 的每个相邻顶点 u:
        如果 u 未被访问:
            DFS(u)

邻接矩阵实现DFS

void DFS(int vertex) {
    visited[vertex] = true;  // 标记当前顶点为已访问
    printf("%d ", vertex);   // 输出当前顶点

    // 遍历所有顶点，访问与当前顶点相连且未访问的顶点
    for (int i = 0; i < numVertices; i++) {
        if (graph[vertex][i] != 0 && !visited[i]) {
            DFS(i);  // 递归访问
        }
    }
}

时间复杂度

• 时间复杂度 : $O(V^2)$，其中 V 是顶点数。因为邻接矩阵需要遍历每一行来查找邻接点。
• 空间复杂度 : $O(V^2)$，用于存储邻接矩阵。

示例：

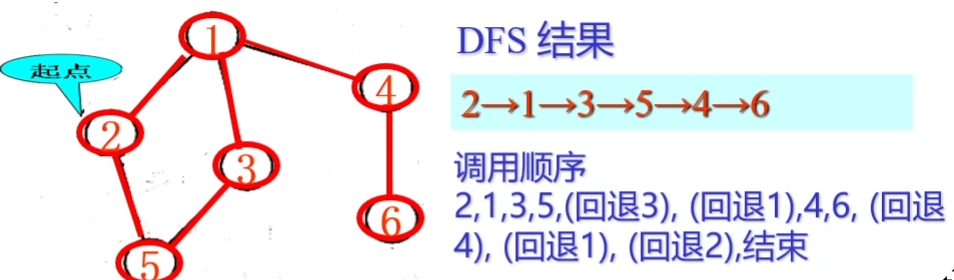
图的邻接表进行DFS

// 深度优先搜索
void DFS(Graph* graph, int vertex) {
    graph->visited[vertex] = true;  // 标记当前顶点为已访问
    printf("%d ", vertex);          // 输出当前顶点

    Node* temp = graph->adjList[vertex];  // 遍历邻接表
    while (temp) {
        int connectedVertex = temp->vertex;
        if (!graph->visited[connectedVertex]) {
            DFS(graph, connectedVertex);  // 递归访问未访问的邻接点
        }
        temp = temp->next;
    }
}

时间复杂度

• 时间复杂度 : $O(V + E)$，其中 $V$ 是顶点数，$E$ 是边数。
• 空间复杂度 : $O(V + E)$，存储邻接表和递归调用栈。

广度（宽度）优先遍历（BFS）

BFS的基本思想

1. 将起始顶点标记为已访问，并入队。
2. 当队列不为空时，执行以下操作：

• 从队列中取出一个顶点。
• 遍历该顶点的所有邻接顶点，若邻接顶点未被访问：
• 将其标记为已访问。
• 将其入队。

3. 若队列为空，算法结束。

邻接表实现BFS

// BFS 实现
void BFS(Graph* graph, int startVertex) {
    Queue* queue = createQueue();

    // 标记起始顶点并入队
    graph->visited[startVertex] = true;
    enqueue(queue, startVertex);

    while (!isEmpty(queue)) {
        int currentVertex = dequeue(queue);
        printf("%d ", currentVertex);  // 访问顶点

        // 遍历邻接顶点
        Node* temp = graph->adjLists[currentVertex];
        while (temp) {
            int adjVertex = temp->vertex;
            if (!graph->visited[adjVertex]) {
                graph->visited[adjVertex] = true;
                enqueue(queue, adjVertex);
            }
            temp = temp->next;
        }
    }
    free(queue);
}

时间复杂度

• $O(V+E)$