静态查找表笔记
每日一言
A person can change, at the moment when the person wishes to change. – Haruhi Fujioka
from Ouran High School Host Club
查找表
基本概念
查找表:同一类型的记录(数据元素)的集合。
关键字:记录(数据元素)中的某个数据项的值。
主关键字:该关键字可以唯一地标识一个记录。
次关键字:该关键字不能唯一标识一个记录查找: 指定某个值,在查找表中确定是否存在一个记录,该记录的关键字等于给定值
静态查找表:对查找表的查找仅是以查询为目的,不改动查找表中的数据
动态查找表:在查找的过程中同时插入不存在的记录,或删除某个已存在的记录。
查找成功:查找表中存在满足查找条件的记录
查找不成功:查找表中不存在满足查找条件的记录
内查找:整个查找过程都在内存中进行,即全部数据元素均在内存
外查找:在查找过程中需要访问外存,即数据元素需要分段读入内存查找
平均查找长度ASL(Average Search Length):查找方法时效的度量为确定记录在查找表中的位置,需将关键字和给定值比较次数的期望值。
在无法确定查找成功和查找不成功的概率分别为多少时,按查找成功时的ASL和查找不成功时的ASL分别计算和讨论。
平均查找长度ASL
查找成功时,asl 为查找的平均查找长度:
$$
ASL = \sum_{i=1}^n p_i c_i
$$- n : 记录的个数
- p_i : 查找n个不同记录中第i个记录的概率(一般默认p_i = 1/n)
$$
\sum_{i=1}^n p_i = 1
$$ - c_i : 找到第i个记录所需的比较次数
查找失败时,按查找失败时实际的比较次数算。
静态查找表
顺序表的查找
从前往后找
1 | |
从前向后遍历时,需要注意判别数组边界,防止指针越界。由于0 下标处我们没有存放数据,我们可以利用0下标来去除判别越界。
从后往前找
1 | |
1 | |
我们将待查找的key值放到数组中下标为0的位置,然后从后向前遍历,返回找到时的下标,那么当找到时就会返回一个非0数,找不到时就会返回0。 下标0 像哨兵一样看守着数组的下届,所以不会越界。
添加监视哨
对于从前向后的顺序查找,我们也可以添加一个哨兵位来提高查找效率:
1 | |
通过监视哨,可以大大提高查找效率。
顺序表的ASL
查找成功时:
$$
ASL_s(n) = \sum_{i=1}^n P_i C_i = (1+2+…+n)/n = (n+1)/2
$$查找失败时:
$$
ASL_f = n+1
$$
有序表查找
顺序查找
对于有序表的查找仍可以通过顺序查找的方式,而且也可以通过设置哨兵的方式来提高查找效率:
- 从前向后查找,哨兵设在尾部,当r[i]>=key时结束
- 从后向前查找,哨兵设在头部,当r[i]<=key时结束
二分查找法
非递归法:
1 | |
递归法:
1 | |
静态树表查找
静态最优查找树
定义:查找性能最佳的判定树。
性质:带权内路径长度之和PH为最小值。(PH与ASL值成正比,即ASL值最小)
$$
PH = \sum_{i=1}^n w_i h_i
$$
- n : 二叉树上结点的个数(有序表长度)
- h : 第 i 个结点在二叉树上的层次数
- w = cp :
- c : 为某个常数
- p : 第 i 个结点的查找概率
最优查找体现的原则:
- 最先访问的结点应该时访问概率最大的结点。
- 每次访问应使结点两边尚未访问的结点的被访问概率之和尽可能相等。
由于没有有效的方法可以快速的构造一颗最优查找树,所以通常我们构建次优查找树。
次优查找树
构造次优查找树的方法
找到最小Δp_i
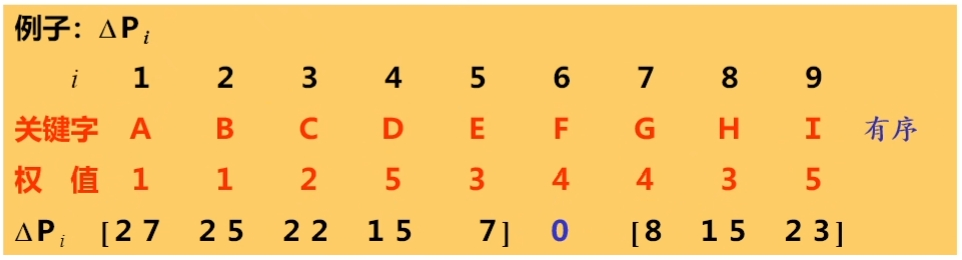
对于有序排列的数据,Δp_i 的计算公式如下:
$$
\Delta p_i = \left| \sum_{j=i+1}^h w_j - \sum_{j=1}^{i-1} w_j \right|
$$一言以概之即为:用比该关键字大的所有数据的权值和 - 比该关键字小的所有数据的权值的和。
找到最小Δp_i 对应的 i ,然后比较相邻数据的权值,若相邻关键字的权值更大,则以权值大的记录位置i,代替最小 Δp_i 的对应的 i(ppt上这句话非常抽象,我觉得意思大概就是以权值更大的相邻项的i 来代替我们找到的i,即以这个权值更大的i来作为我们当前构造树的根结点)
递归处理r_i 的左子树构造次优查找树
递归处理r_i 的右子树构造次优查找树
化简计算Δp_i 的方法

次优查找树上的查找步骤
通过递归查找。把根结点作为当前考察的结点
- 若当前结点为空,则返回空指针
- 将当前结点的key 与查找K比较:
- K== key 返回当前结点;
- K > key 递归其左子树;
- K < key 递归其右子树;
比较次数不超过树的深度 O(log n)
分块查找(块间有序,块内无序)
分块有序,即分成若干子表,要求每个子表中的数值都比后一块中数值小(但子表内部未必有序)。
然后将各子表中的最大关键字构成一个索引表,表中还要包含每个子表的起始地址(即头指针)。
示例如下:
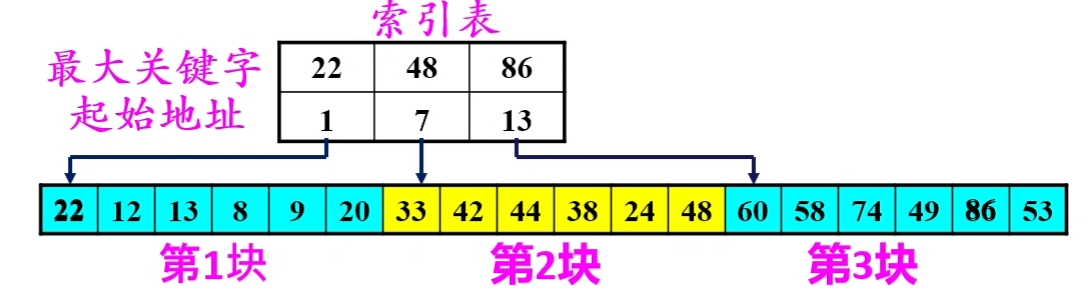
查找:
- 对索引表使用折半查找法(索引表有序)
- 确定了待查关键字所在的子表后,在子表内采用顺序查找法(子表无序)