计算机系统基础第四次作业及练习题

3.63

1. 首先我们查看switch部分的第一代码：sub $0x3c,%rsi %rsi-=60; 我们可以知道跳转表中第一个位置对应的数即为60，且跳转表中一共有6个地址，则switch中最大的数应该为65
2. 然后我们根据 ja 4005c3 当%rsi>5时，就跳转到地址 4005c3 所以该地址应该为default 的地址。
3. 最后我们把每个地址中的汇编代码转化为c代码。

• 0x4005a1:

  result*=8;
  return result;

• 0x4005c3:

  result+=75;
  return result;

• 0x4005aa:

  return result>>3;

• 0x4005b2:

  result =<< 4;
  result -= x;
  result*=result;
  return result+75;

• 0x4005bf:

  result*=result;
  return result+75;

这样我们就得到了完整的函数c代码：

long switch_prob(long x, long n) {
    long result = x;
    switch(n) {
        case 60:
            result = x * 8;
            break;
        case 62:
            result  = x*8;
            break;
        case 63:
            result >>= 3;
            break;
        case 64:
            result <<=4;
            result -= x;
        case 65:
            result *= result;
            result += 75;
            break;
        default:
            result += 75; 
    }
    return result;
}

3.66

这一题需要我们反向计算出NR(n)和NC(n)的值，根据题目已知信息该函数计算矩阵的j列的和。我们分析汇编代码的前几行代码：

leaq 1(,%rdi, 4), %r8
    leaq (%rdi,%rdi, 2), %rax
    testq %rax, %rax
    jle L4

以及L4的代码：

.L4:
    movl $0, %eax
    ret

当 %rax <=0时，就不会进入循环，这里的 %rax = 3*n 就是NR(n)的定义，所以得到：

#define NR(n) 3*n

然后我们看循环内部的代码：

.L3:
    addq (%rcx), %rax	//%rax += *(%rcx)
    addq $r8, %rcx	//%rcx += %r8
    addq $1, %rdx	//%rdx += 1
    cmpq %rdi, %rdx	//判断循环终止
    jne .L3
    rep; ret

我们可以知道 %rcx 存储的即为每一行 j 列元素的地址，%rax为result。由于c语言中二维数组以行为主序，所以 %8 就是NC(n) 的定义。%r8 = （4n+1）*8 8为long 类型的宽度。所以NC的定义为：

#define NC(n) 4*n+1

3.64

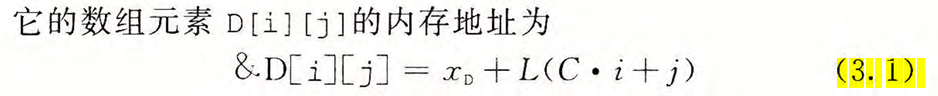等式（3. 1）如图所示， 假设数组D的定义为D[R][S][T]，则D[i][j][k] 的地址为：

A：&D[i][j][k] = D + L*( T*(S*i + j) + k)

B:

store_ele:
    leaq (%rsi,%rsi,2), %rax
    leaq (%rdi,%rax,4), %rax 	//%rax = 13j
    salq $6, %rsi
    addq %rsi, %rdi		//%rdi = 65i
    addq %rdi, %rdx		//%rdi = 65i + 13j
    addq %rax, %rdi		//%rdx = 65i +13j + k
    movq A(%rdx,8), %rax	//%rax = *(8*(13*(5*i +j) + k))
    movq %rax, (%rcx)
    movl $3640, %eax
    ret

根据A推出的公式，得到：

• S = 5
• T = 13
• R = 3640 /8/65 = 7

3.69

A.

第一句汇编代码 mov 0x120(%rsi),%esi 我们根据b_struct的声明可以得知 bp->last 的地址为 bp + 288;

由于由于 bp->a 的首地址为：bp + 8 所以 bp->a 所占的空间为280个字节。

通过

lea	(%rdi,%rdi,4),%rax	//%rax = 5i
lea	(%rsi,%rax,8),%rax	//%rax = bp + 40i

我们可以知道a的一个结构体所占的空间为40个字节，所以我们可以得到：

• CNT = 280 / 40 = 7

B.

我们看剩下的汇编代码：

mov 0x8(%rax),%rdx 	//%rdx = ap->idx
movslq %ecx,%rcx
mov %rcx,0x10(%rax,%rdx,8)	// *(bp + 40i + 16 + (ap->idx)*8 ) = n 

我们可以得知a_struct中，第一个元素 idx 占16个字节，x 是个数组，每个元素占8个字节，结合题目所存取的数都是有符号数。所以我们得到a_struct 的完整声明如下：

typedef struct a_struct
{
    long long idx;
    int x[3];
}

练习题

3.1

答案：

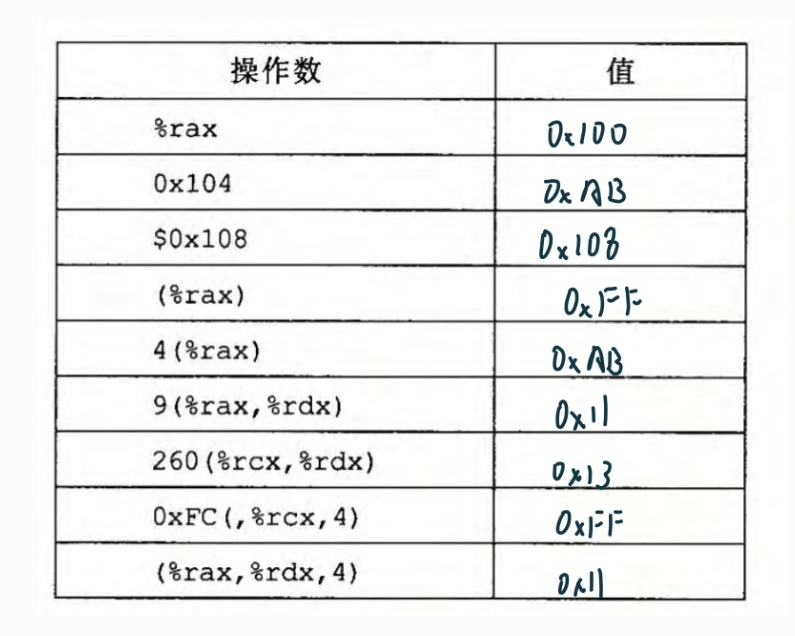
3.2

在写后缀时，似乎是在两个操作数中选取小的那个操作数的大小作为赋值的大小

1. movl %eax 大小4个字节，所以为双字 l
2. movw %dx 大小为2个字节，所以为单字w
3. movb $0xFF 为一个字节，为一个字节b
4. movb %dl 大小为一个字节，为b
5. movq 两个操作数都为四字，为q
6. movw %dx为字，为w

3.3

1. %ebx 只有寄存器前4个字节的信息， 但是64位机器中内存中地址需要8个字节表示。
2. movl只能赋值4个字节的信息，%rax和（%rsp）有8个字节长,指令后缀与寄存器ID不匹配
3. 源和目的不能都是内存
4. 没有寄存器 %sl
5. 无法把一个立即数当作目标
6. 目标地址的大小不正确
7. 指令后缀与寄存器id不匹配，%si为双字，b表示一个字节的赋值

3.4

在小到大的转化时，我们通过指令movz类或movs类来进行：movz进行无符号扩充，movs进行有符号扩充；

在大到小的转化中，我们直接使用 mov类，截断高位数据。

1. char -> int

   movsbl	(%rdi),%eax
   movl	%eax, (%rsi)

2. char ->unsigned

   movzbl	(%rdi),%eax
   movl	%eax, (%rsi)

3. unsigned char -> long(应该维持原先的无符号数的值不变)

   movzbl	(%rdi),%eax	//读一个字节并进行0扩位
   movq	%rax,(%rsi)

4. int -> char

   movl	(%rdi),%eax
   movb	%al,(%rsi)

5. unsigned -> unsigned char

   movl	(%rdi),%eax
   movb	%al,(%rsi)

6. char -> short

   movsbw	(%rdi),%ax
   movw	%ax,(%rsi)

3.6

1. x +6 (题目有误，%ax应为 %rax)
2. x + y
3. x + y*4
4. x + 8*x + 7 = 9 *x +7
5. 4*y + 10
6. x + y * 2 +9

2.21

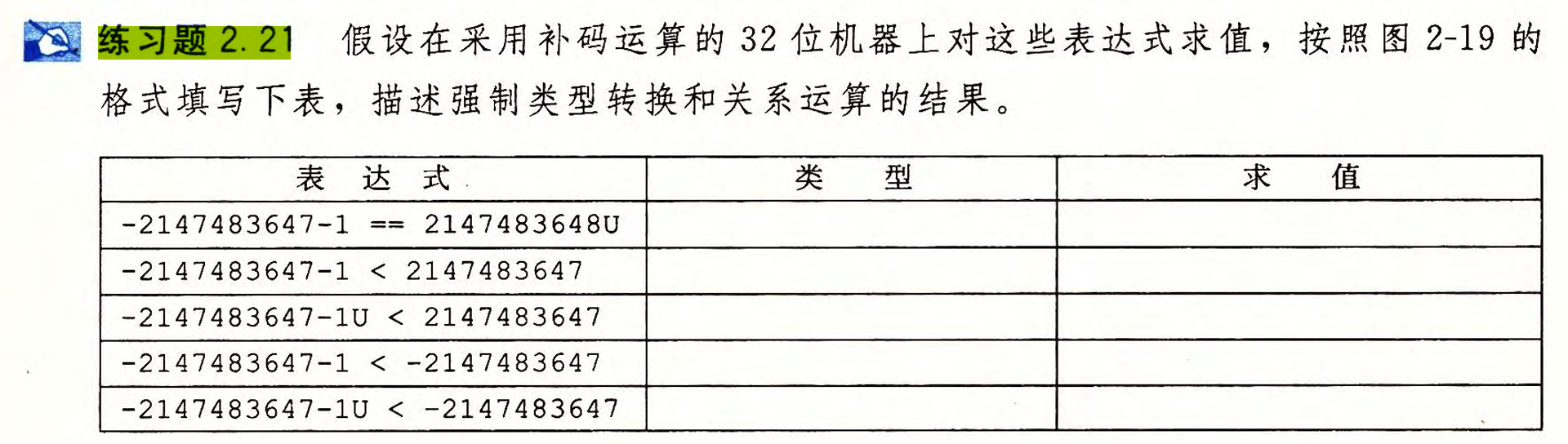
如果有任何一个运算数是无符号的，那么在比较之前，另一个运算数会被强制类型转换为无符号数。

类型	求值
无符号	1
有符号	1
无符号	0
有符号	1
无符号	1

• 第一个数为-2147483648 转为无符号数为2147483648 == 2147483648 所以求值为1
• 第一个数-2147483648 ，第二个数为2147483647 两侧都为有符号数，求值为1
• 第一个数为-2147483648，转为无符号数为2147483648，因该>2147483647 求值为 0
• 第一个数为-2147483648，第二个数为-2147483647，都为有符号数直接求值为1
• 第一个数为-2147483648，转为无符号数为2147483648，第二个数为-2147483647,转为无符号数为2147483649 > 2147483648 所以求值为 1

2.23

首先我们先将每个函数执行后的二进制码写出来：

w	fun1(w)	fun2(w)
0x00000076	0x00000076	0x00000076
0x87654321	0x00000021	0x00000021
0x000000C9	0x000000C9	0xFFFFFFC9
0xEDCBA987	0x00000087	0xFFFFFF87

然后我们再把他们转化成10进制整数：

w	fun1(w)	fun2(w)
0x00000076	118	118
0x87654321	33	33
0x000000C9	201	-55
0xEDCBA987	135	-121

2.24

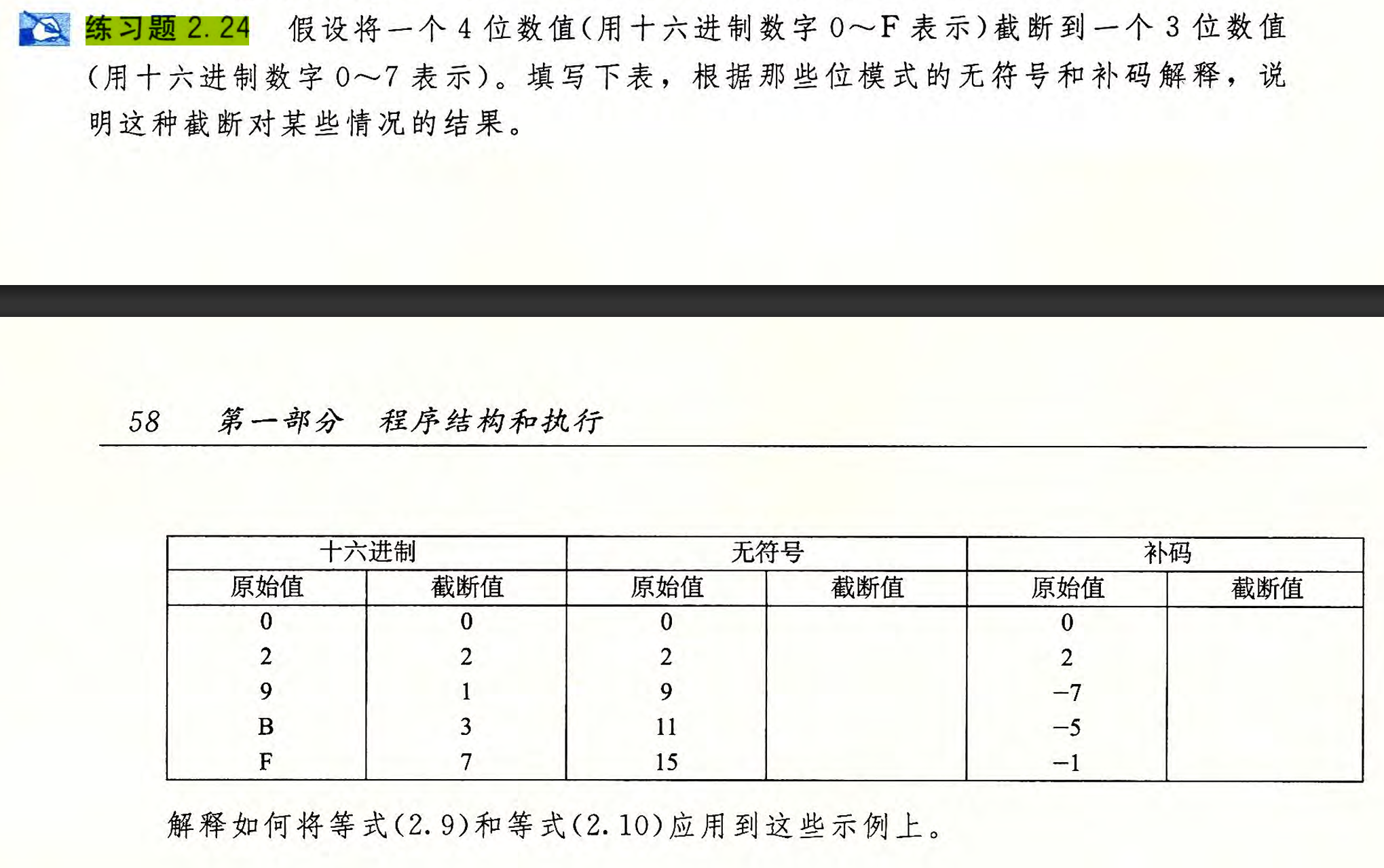
首先来看无符号数：无符号数的截断与16进制直接截断相同

原始值	截断值
0(%8)	0
2(%8)	2
9(%8)	1
11(%8)	3
15(%8)	7

然后来看有符号数：

原始值	截断值
0->0(%8)	0
2->2(%8)	2
(-7)-> 9(%8)	1
-5->11(%8)	3
-1->15(%8) = 7 (-2^4)	-1

等式（2. 9）：

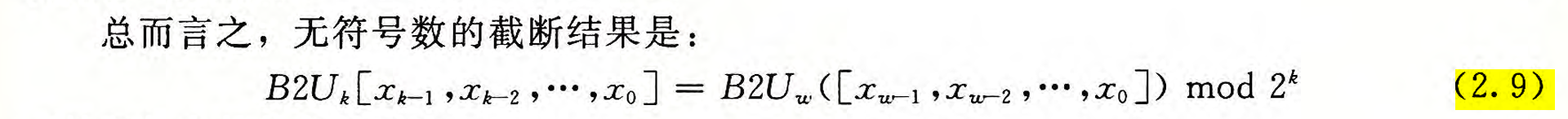
等式（2.10）：

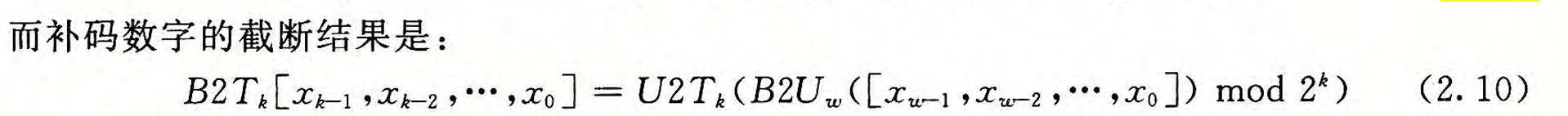
2.33

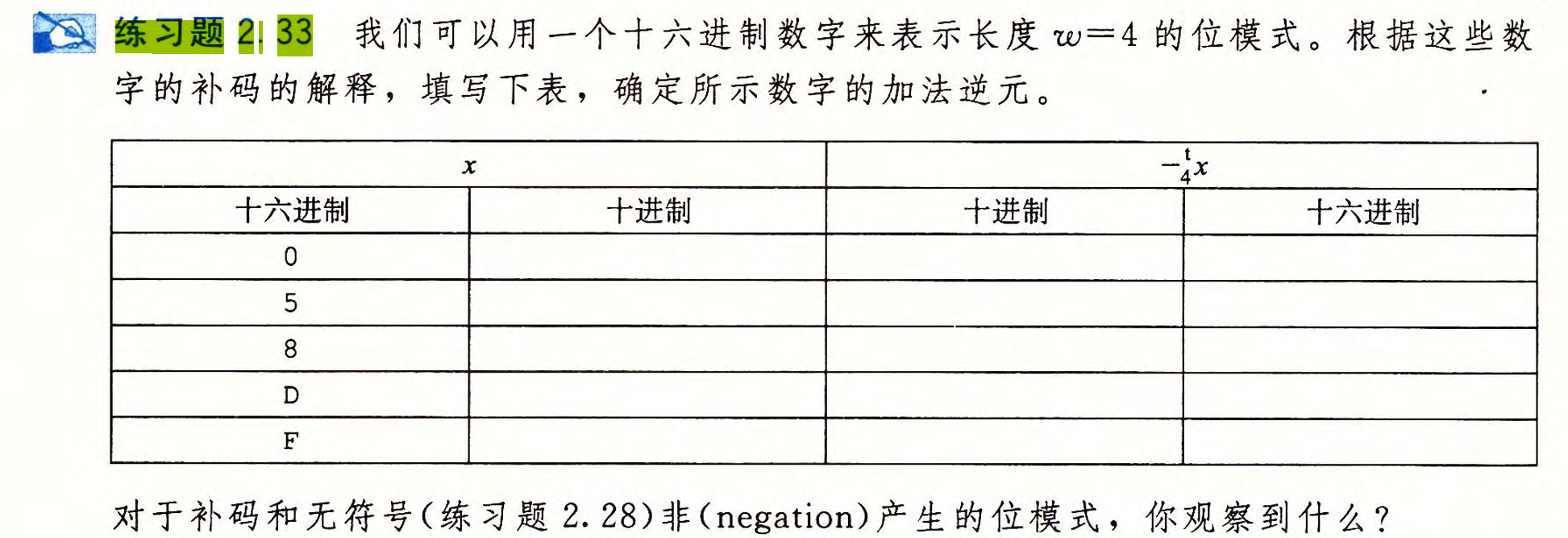
16进制	10进制	10进制	16进制
0	0	0	0
5	5	-5	B
8	-8	8	8
D	-3	3	3
F	-1	1	1

通过16进制观察可能不明显：我们把左右两列变成2进制观察：

col1	col2
0000	0000
0101	1011
1000	1000
1101	0011
1111	0001

加法逆元的的二进制位等于取反+1，使得a + （-a） 后刚好进位溢出1，使得有效位全部为0。

2.40

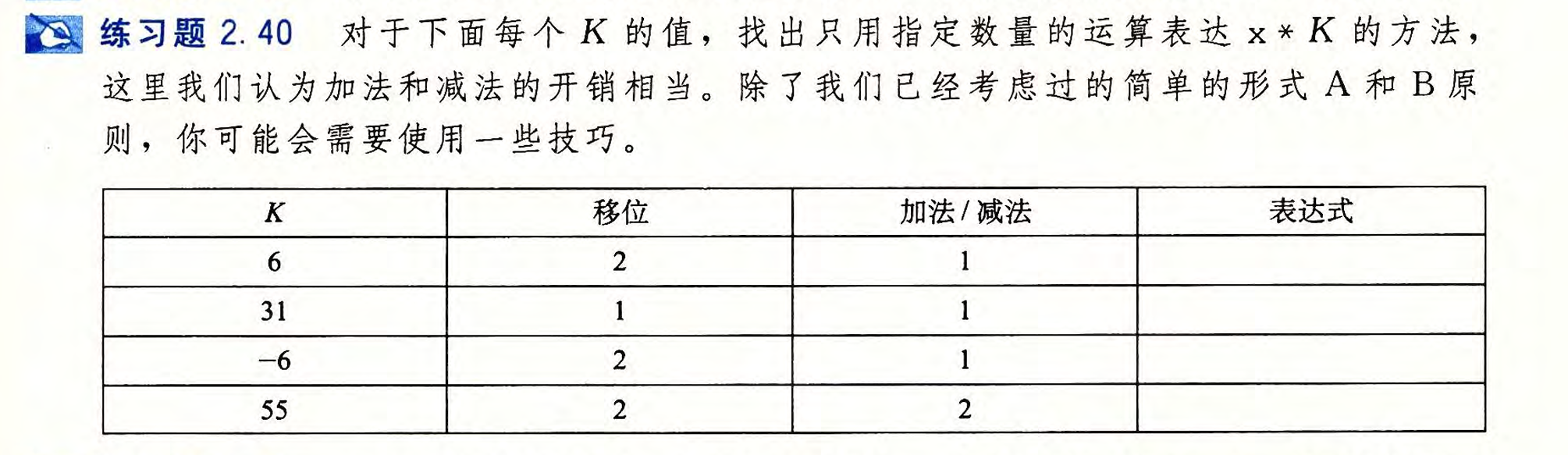
表达式
(x<<2) + (x<<1)
(x<<5) - x
(x <<1) - (x<<3)
(x<<6) - (x<<3) -x

2.45

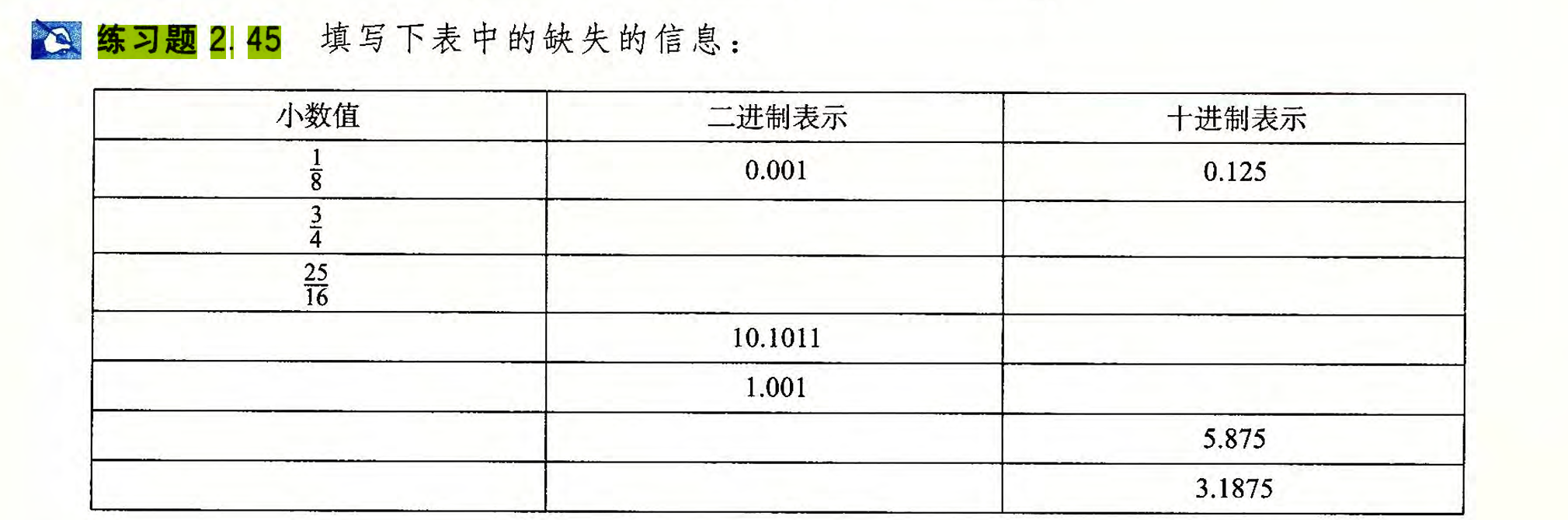
小数值	二进制表示	十进制表示
1/8	0.001	0.125
3/4	0.11	0.75
25/16	1.1001	1.5625
43/16	10.1011	2.6876
9/8	1.001	1.125
47/8	101.111	5.875
51/16	11.0011	3.1875

2.47

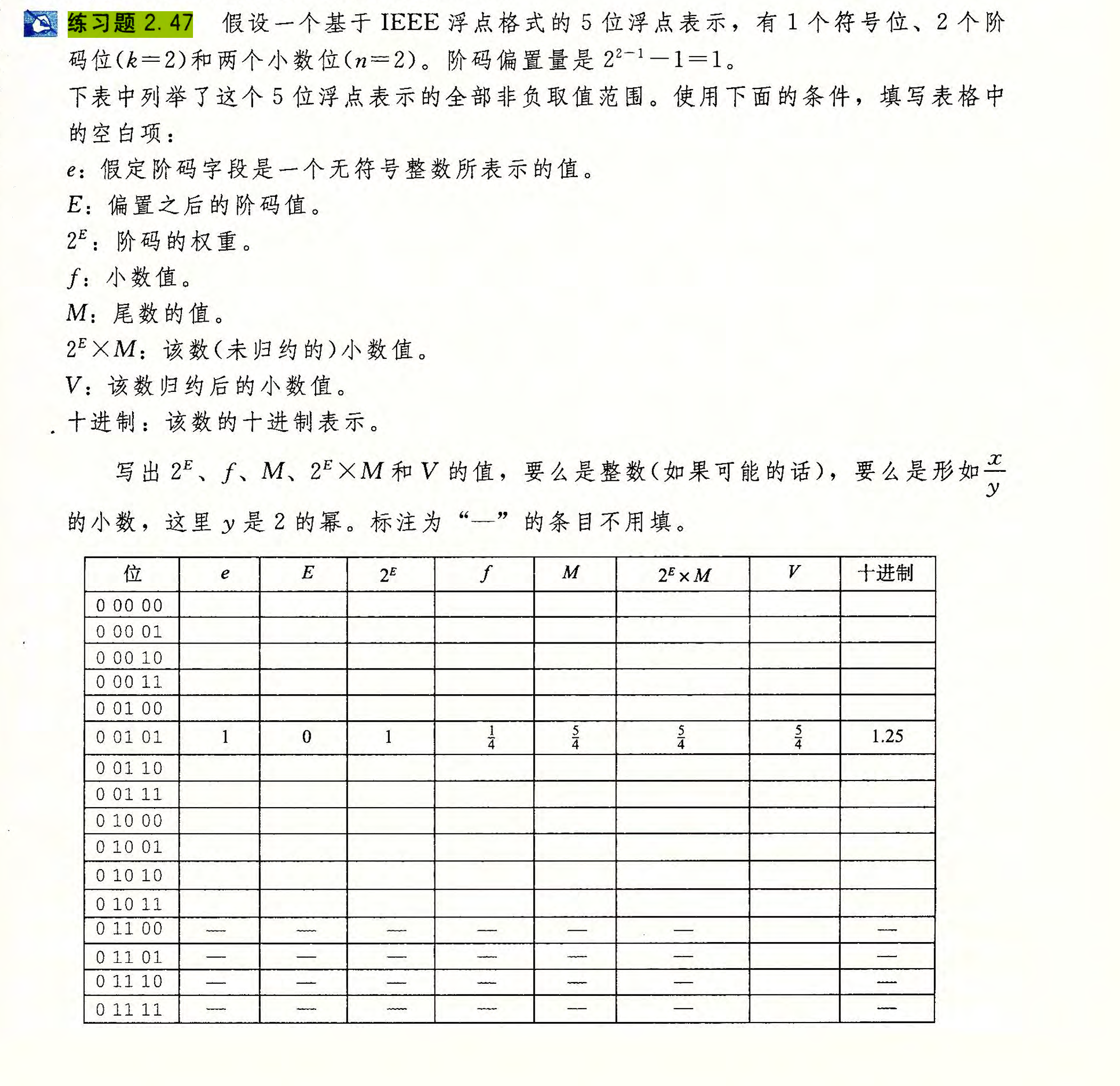
位	e	E	2^E	f	M	(2^E) * M	V	十进制
0 00 00	0	0	1	0/4	0/4	0/4	0	0
0 00 01	0	0	1	1/4	1/4	1/4	1/4	0.25
0 00 10	0	0	1	2/4	2/4	2/4	1/2	0.5
0 00 11	0	0	1	3/4	3/4	3/4	3/4	0.75
0 01 00	1	0	1	0	1	1	1	1.0
0 01 01	1	0	1	1/4	5/4	5/4	5/4	1.25
0 01 10	1	0	1	2/4	6/4	6/4	3/2	1.5
0 01 11	1	0	1	3/4	7/4	7/4	7/4	1.75
0 10 00	2	1	2	0	1	2	2	2.0
0 10 01	2	1	2	1/4	5/4	5/2	5/2	2.5
0 10 10	2	1	2	2/4	6/4	6/2	3	3.0
0 10 11	2	1	2	3/4	7/4	7/2	7/2	3.5
0 11 00	–	–	–	–	–	–	正无穷	–
0 11 01	–	–	–	–	–	–	NaN	–
0 11 10	–	–	–	–	–	–	NaN	–
0 11 11	–	–	–	–	–	–	NaN	–