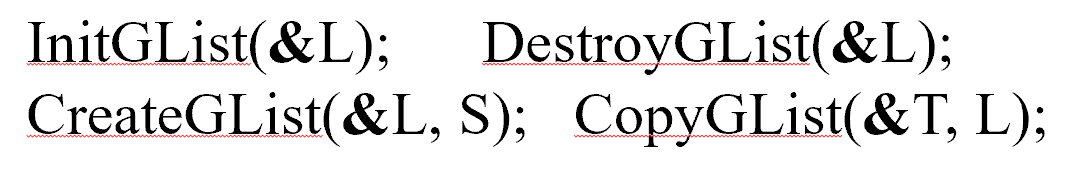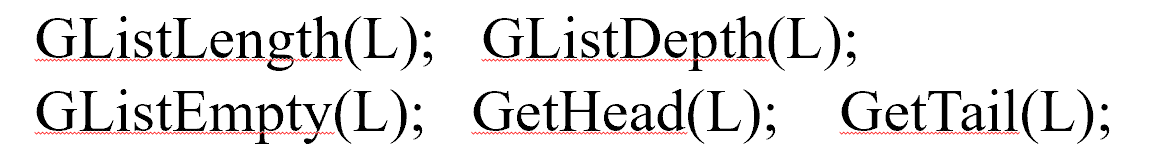数组和广义表

数组

数组是线性表的扩展，其数据元素本身也是线性表。

数组的特点

• 数组中各元素都具有统一的类型
• 可以认为，d维数组的非边界元素具有d个直接前驱和d个直接后继
• 数组维数确定后，数据元素个数和元素之间的关系不再发生改变，适合于顺序存储。
• 每组有定义的下标都存在一个与其相对应的值

数组的基本操作定义

1. 构造n维数组
2. 销毁数组
3. 取得指定下标的数组元素值
4. 为指定下标的数组元素重新赋值

多维数组的通用操作

通过结构体对于结构体的维度以及每个维度的长度进行封装：

typedef struct{
    ElemType * base
    int dim;
    int* bounds;
    int* constans;
}Array;

数组的顺序存储结构

一维数组

ElemType a[n]

以基地址开始申请的连续n个空间，数组名a即为基地址

若要找到第 i 个元素：

1. a[i] = a + i * sizeof(ElemType);

二维数组

ElemType   a[m][n];

一般情况下，我们以第一个参数(m)为行，以第二个参数(n)为列。

在Pascal、c等语言中，对于二维数组的存取方式为以行为主序，将二维数组在内存中以一行为一个单位顺序存储。

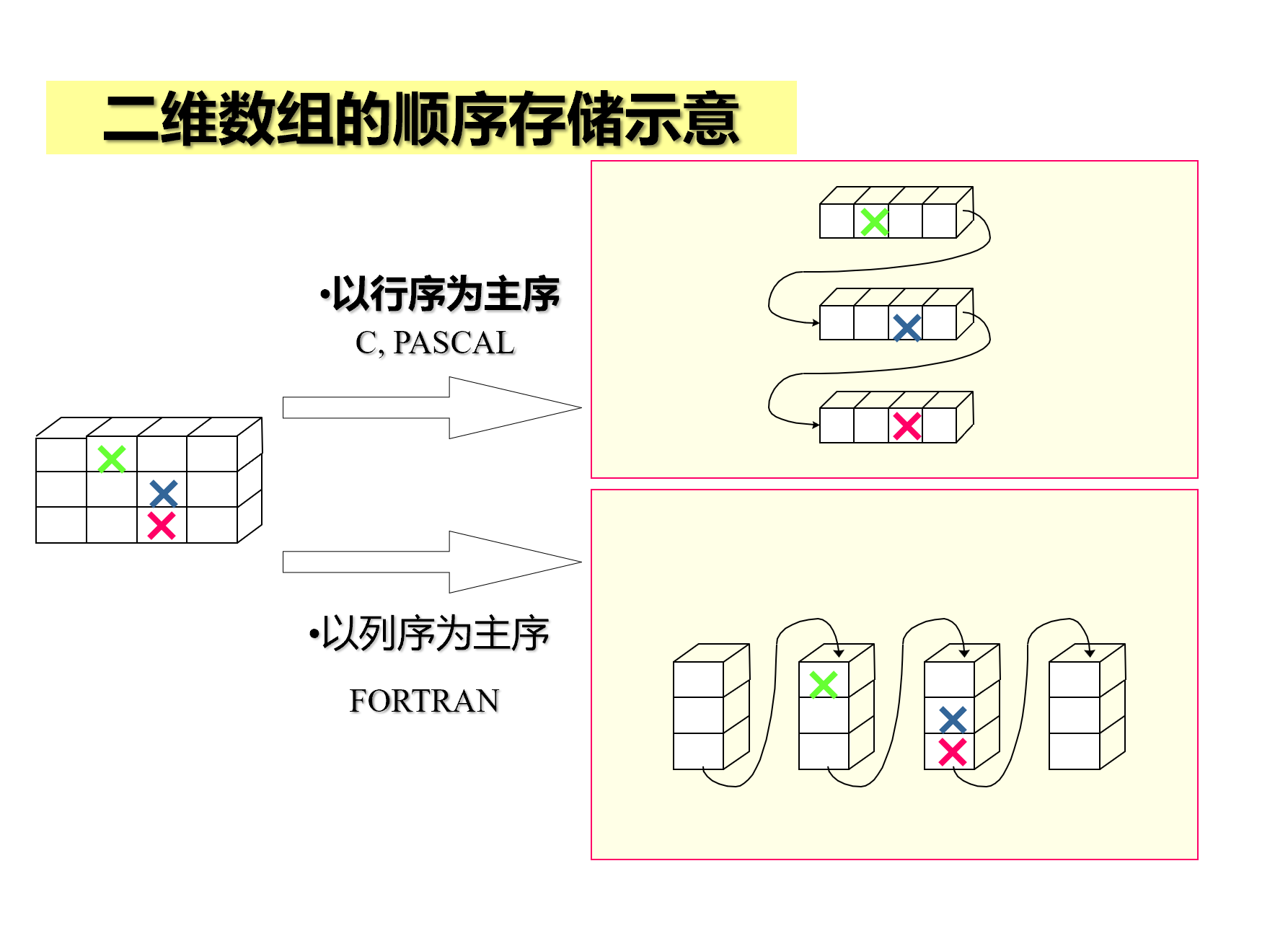
在以行为主序存储的二维数组中，若要找到a[i][j]:

• a[i][j] = a + (i * n + j)*sizeof(ElemType)

矩阵的压缩存储

目的是节省空间

对称矩阵

特点：

• A[i][j] = A[j][i]
• 行数和列数相等即 n*n

存储方法：

我们只需要存储下/上三角(包括主对角线)的数据元素。对于一个n*n 的矩阵来说总共占用 n(n+1)/2 的空间。

a[1][1]	a[2][1]	a[2][2]	……	a[i][j]	……	a[n][n]

三角矩阵

特点：

• 行数和列数相等即 n*n
• 主对角线以下/上的元素（不包括对角线）全部为一个常数c

存储方法：

重复元素c共享一个元素存储空间，共占用n(n+1)/2+1个元素空间

c	a[1][1]	a[2][1]	a[2][2]	……	a[i][j]	……	a[n][n]

带状矩阵（对角矩阵）

特点：

• 行数和列数相等即 n*n
• 非零元素集中在主对角线及其两侧共L(奇数)条对角线的带状区域内——L对角矩阵

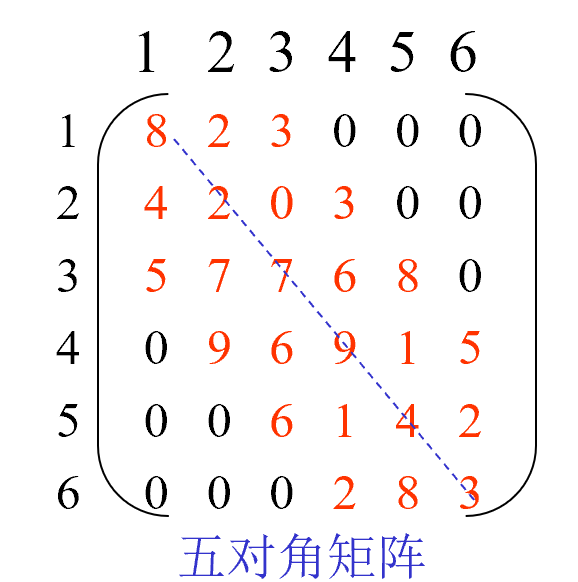
存储方法：

只存储带状区内的元素。除首行和末行，按每行L个元素，共 (n-2)L+(L+1)=(n-1)L+1 个元素。

• 首行+末行 = L+1

随机稀疏矩阵

特点：

• 大多数元素为零

常用存储方法：

• 记录每一非零元素(i,j,value)——虽然节省空间，但丧失随机存取功能
  • 顺序存储：三元组表
  • 链式存储：十字(正交)链表

三元组表

#define MAXSIZE   1000  //设定非零元素最大值
typedef   struct  {
	int    i, j ;
	ElemType   e;
}Triple;
typedef  struct {
	Triple  data[MAXSIZE+1];	//三元组表，data[0]未用
	int    mu, nu, tu;	//行数、列数、非零元个数
}TSMatrix;

求转置矩阵

三元组表中，我们默认以行为主序进行存储，所以转置过后我们仍然需要维持三元组表的行主序原则。

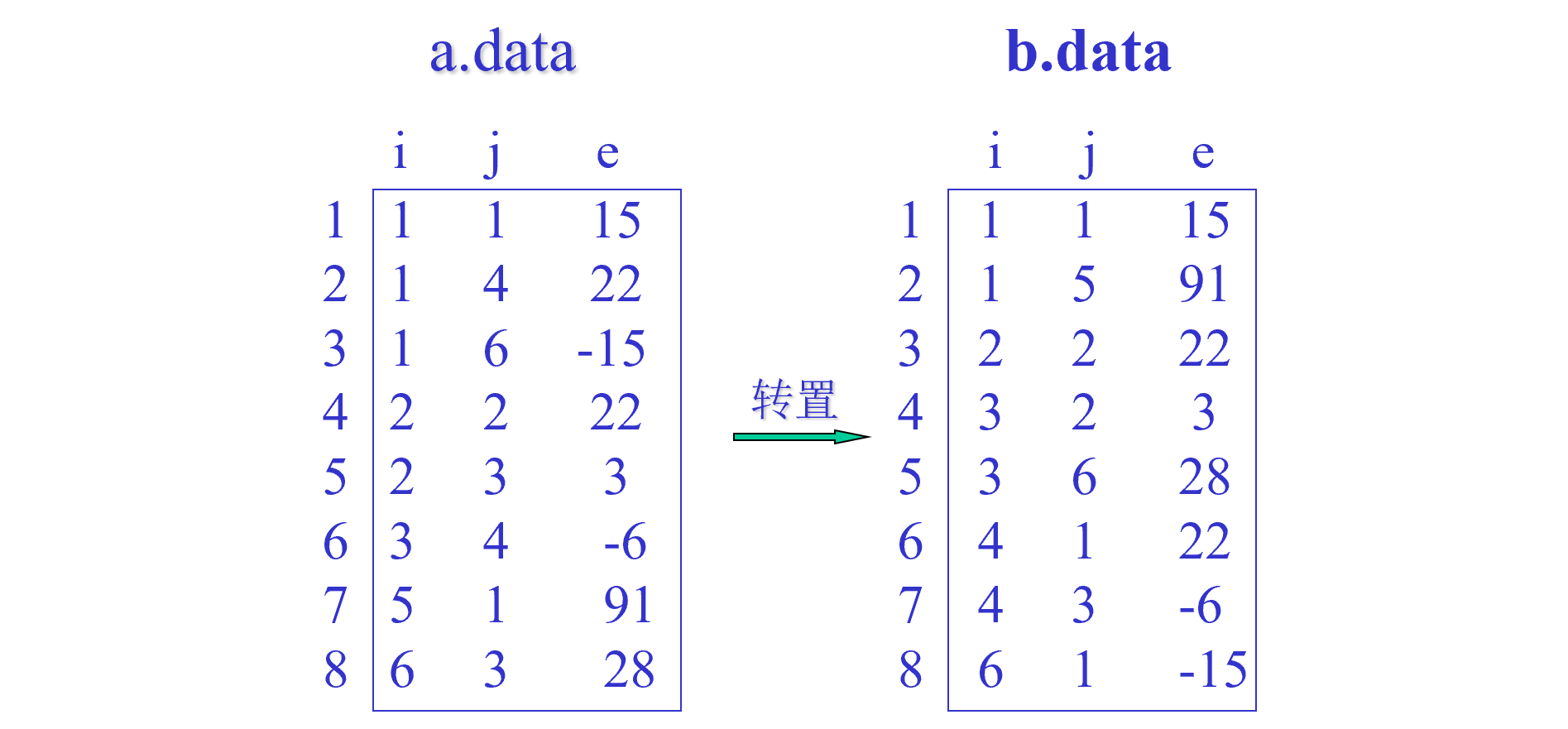
算法一 O(n*t)

void TransMatrix(TSMatrix &b,  TSMatrix a)
{  
    b.mu=a.nu;  //b的行数等于a的列数
    b.nu=a.mu;  //b的列数等于a的行数
    b.tu=a.tu;  //b的非零元个数等于a的非零元个数
    if  (b.tu)  //非零元素个数不为零
    {
        int q=1;    //指示b中存放数据的位置，初值为1
        for (int row=1; row<=b.mu;  row++ )     //对b的每一行进行填充
            for (int p=1; p<=a.tu;  p++ )        //对a的每个三元组检查
                if  (a.data[p].j==row) {    //找行号为row的三元组放入b中
                    b.data[q].i =a.data[p].j; 
                    b.data[q].j =a.data[p].i;
                    b.data[q].e =a.data[p].e;
                    q++;                   //修正q值
                }
        }
} //TransMatrix

快速转置法 O(n+t)

bool FastTransMatrix(TSMatrix &b,  TSMatrix a)
{  
    b.mu=a.nu,  b.nu=a.mu,  b.tu=a.tu;
    int num[a.nu+1] = {0}, //num存放矩阵a中每一列的非零元个数
    cpot[a.nu+1],   //cpot存放矩阵a中每列的第一个非零元素在b中的位置
    col, t, p, q;
    if( b.tu )
    {	                
        for (t=1; t<=a.tu; ++t)
            ++num[a.data[t].j];     //统计a中每列有几个非零元素   
        cpot[1]=1;  //a中第一列第一个元素在b中位置为1
       	for ( col=2; col<=a.nu; ++col ) 
            cpot[col]=cpot[col-1]+num[col-1];   //上一列的第一个元素在b中的位置+上一列的元素个数 = 这一列第一个元素在b中的位置
       	for  ( p=1; p<=a.tu; ++p )
        {   //对a.tu个非零元素转置
            col=a.data[p].j;    //获取当前元素的列
            q=cpot[col];        //获取当前列第一个元素在b中的位置
            //放入对应位置
            b.data[q].i =a.data[p].j;
            b.data[q].j =a.data[p].i;
            b.data[q].e =a.data[p].e;
            //由于第一个位置已经被占用，下一个该列的元素放在下一个位置上
            ++cpot[col] ;
        }
    }
    return trus;  
}//FastTransMatrix

行逻辑链接的表

typedef  struct  {
     Triple  data[MAXSIZE+1];
     int       rpos[MAXRC+1];
     int       mu, nu, tu;
}RLSMatrix;

十字（正交）链表

typedef  struct OLNode
{  
    int  i, j ;
    ElemType  e;
    struct  OLNode  * right, * down;
}OLNode, * OLink;
typedef  struct  {
    OLink   * rhead, * chead;
    int          mu, nu, tu;
}CrossList;

示意图：

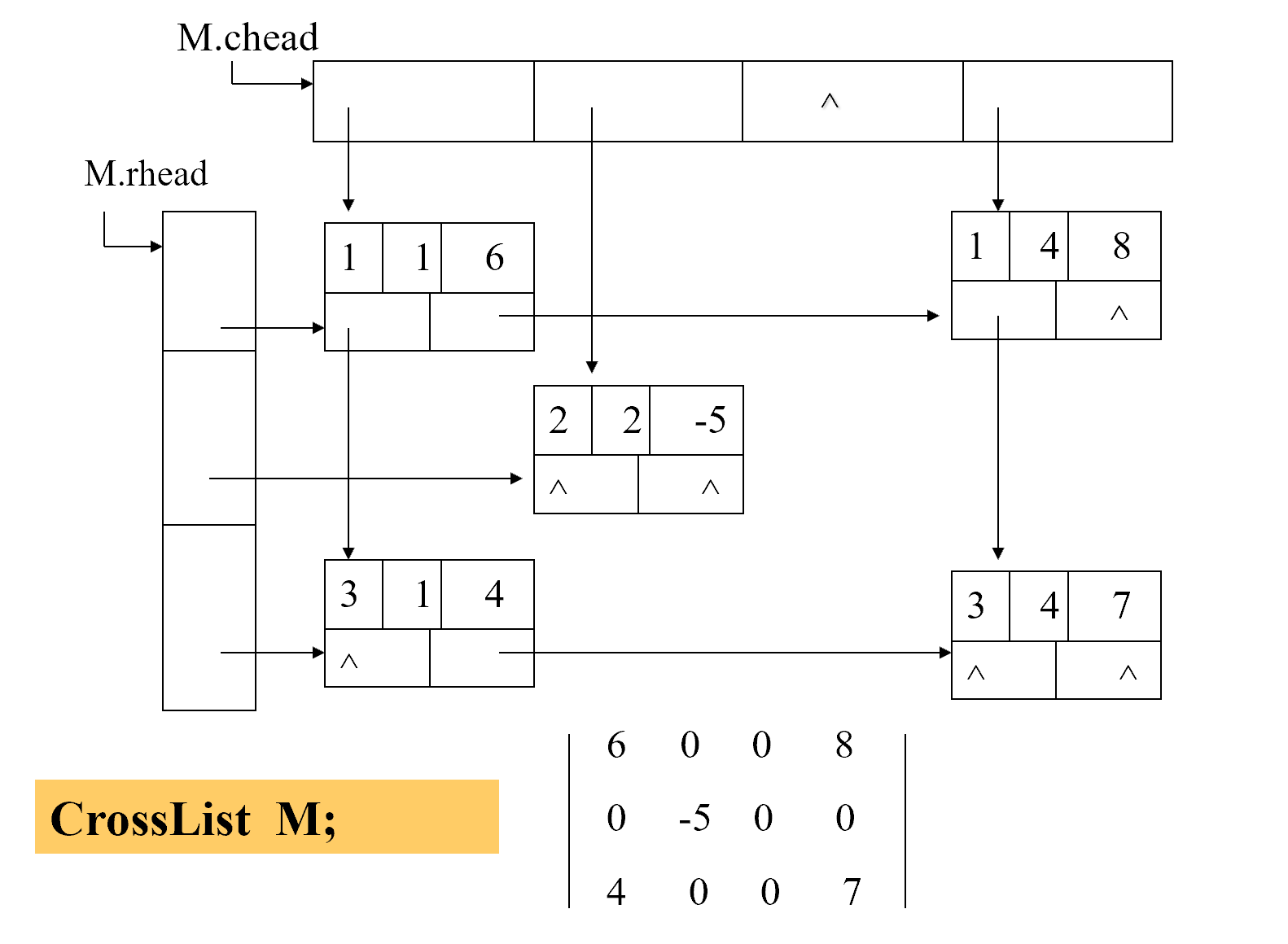
广义表（列表）的定义和表示方法

广义表是由零个或多个原子或者子表组成的有限序列。

• 原子：逻辑上不能再分解的元素。
• 子表：作为广义表中元素的广义表。

广义表中的元素全部为原子时即为线性表。线性表是广义表的特例，广义表是线性表的推广。

相关术语

• 表的长度：表中的元素（第一层）个数。
• 表的深度：表中元素的最深嵌套层数。
• 表头：表中的第一个元素。
• 表尾：除第一个元素外，剩余元素构成的新广义表。

图形表示法

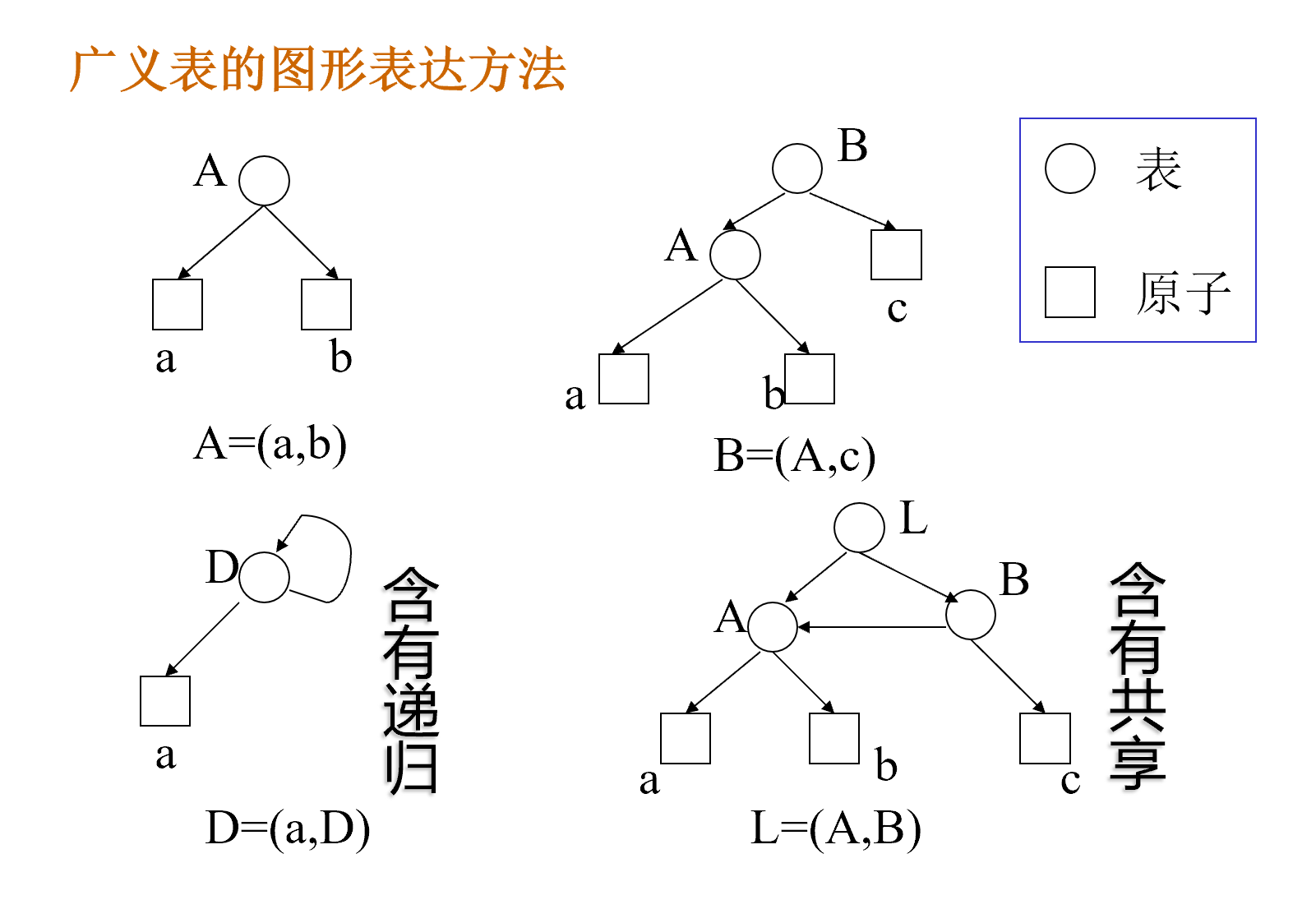
表示方法

广义表结构的分类

• 纯表：与树型结构对应的广义表。
• 再入表：允许结点共享的广义表。
• 递归表：允许递归的广义表。

递归表>再入表>纯表>线性表。

基本操作

• 结构的创建和销毁

  

• 状态函数

  

• 插入和删除操作

  

• 遍历

  

广义表的存储结构

头尾链表形式

typedef enum {ATOM, LIST} ElemTag;
// ATOM==0:原子；LIST==1：子表
typedef struct GLNode{
	ElemTag  tag;
	union {
	    AtomType  atom;
	    struct  {
	        struct GLNode  *hp, *tp;
	    }ptr;
	}
} * GList1;

• tag = 1 为表结点

  

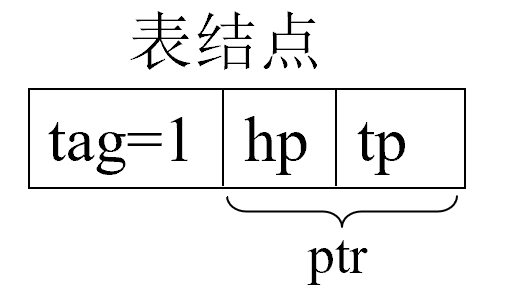
• tag = 0 为原子结点

  

存储结构示意图：{a,{b,c,d}}

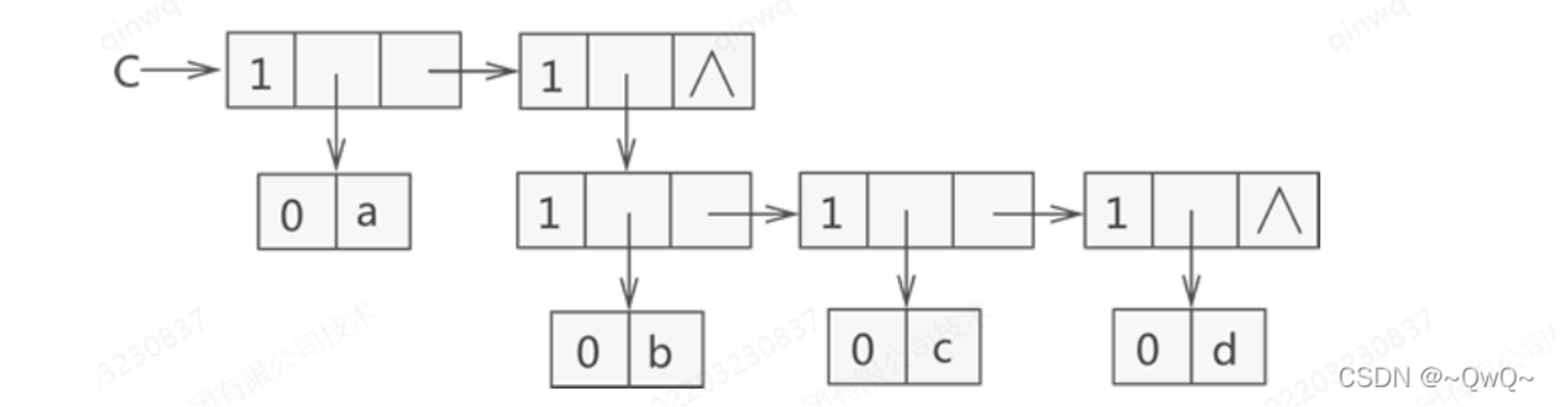
扩展的线性链表形式

typedef enum {ATOM, LIST} ElemTag;
// ATOM==0:原子；LIST==1：子表
typedef struct GLNode{
	ElemTag  tag;
	union {
	     AtomType  atom;
	     struct  {
	          struct GLNode  *hp;
	     }
	}
	struct GLNode  *tp;
} * GList2;

存储结构示意图：{a,{b,c,d}}

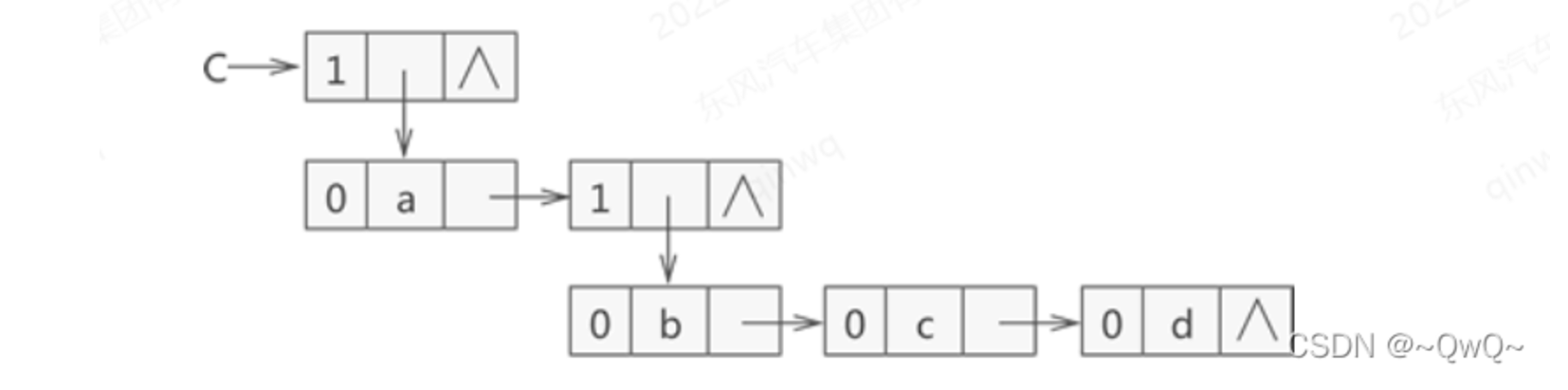
广义表的递归算法

广义表的特点：定义是递归的。

递归求广义表的深度

方法一：分析表中各元素

int GListDepth(GList1 L)
{        if  (!L) return 1;   //空表
          if  (L->tag==ATOM) return 0;  //单原子
          for (max=0, pp=L; pp; pp=pp->ptr.tp) {	//遍历该广义表的每一个元素，取最大深度
                  dep=GListDepth (pp->ptr.hp);
                  if (dep>max) max=dep;
           }
           return  max+1;
 }//GListDepth

方法二：分析表头和表尾

int GListDepth(GList1 L)
{        if  (!L) return 1;   //空表
          if  (L->tag==ATOM) return 0;  //单原子
          dep1=GListDepth (L->ptr.hp)+1;	//计算当前表头的深度
          dep2=GListDepth (L->ptr.tp);		//计算表尾组成的新表的深度，无需+1。
          if  (dep1>dep2)  return dep1;
          else   return  dep2;
 }//GListDepth

总感觉这里有点像孩子兄弟二叉树？？hp结点指向孩子，tp结点指向下一个兄弟

复制广义表

Status CopyGList(GList1 &T, GList1 L)
{        if  (!L) T=NULL;   //复制空表
         else {
            T=(GList1)malloc(sizeof(GLNode));
            if (!T) exit(OVERFLOW);
            T->tag=L->tag;
            if (L->tag==ATOM) T->atom=L->atom; //复制单原子
            else {
                 CopyGList(T->ptr.hp, L->ptr.hp);//复制表头
                 CopyGList(T->ptr.tp, L->ptr.tp);//复制表尾
            }
         }
         return  OK;
 }//CopyGList

对于一个广义表，组成部分只有两部分，表头和表尾。所我们只需要不断的递归复制表头和表尾即可。

对于表头可能是

1. 子广义表
2. 单原子

对于表尾则一定是广义表：

1. 非空广义表
2. 空广义表

所以停止递归的条件有两个：

1. 表头是一个单原子
2. 表头/表尾是一个空表

本章学习要点

最后附上本章学习要点：