赫夫曼树
前瞻概念
- 结点权值:和叶子结点对应的一个有某种意义的实数(Wi)
- 树的路径长度:从树根到每一个结点的路径上的分支数之和。
- 带权路径长度:叶子结点的路径长度与该结点的权之积。
- 树的带权路径长度:树中所有叶子结点的带权路径长度之和。
- 最优二叉树(Huffman,赫夫曼/哈夫曼/霍夫曼树):带权路径长度WPL最小的二叉树。
从最优二叉树这一名字我们就可以得知,在我们提前知道数据的范围权重(个数比时)通过赫夫曼数是查找路径最短的树。
如何构建赫夫曼树
赫夫曼树的特点是,权值越大的结点与根结点的路径越短。根据这一特性,我们构建赫夫曼树的算法如下:
基本算法
- 将所有给定权值当作一棵只有根结点的树,树的左右孩子都是空结点,然后将所有的树放在一个T数组中{T1,T2,……,Tn}生成森林。
- 找到T数组中权值最小的两棵树,生成一颗新树T(n+1),这颗树的左右子结点分别是两颗权值最小的数,根结点的权值为左右子结点的权值之和
- 将T(n+1)加入到数组中,同时删除上一步找到的两颗子树。
- 重复步骤2、3,知道数组中只有一颗子树。
虽说很多教程中说需要删除合并后的子树,但是在实际操作中,我们通常提前创建一个大小为2*n+1大小的数组,将将后续生成的树之间放入到数组中,并且省略删除子树的过程,但是我们通过parent 是否为空结点来判断一棵子树是否已经被合并过了。
所以赫夫曼树的构建可以说是即使用了链式存储,也使用了顺序存储结构。
构建代码
结点定义
1
2
3
4
5
| typedef struct {
unsigned int weight;
unsigned int parent, lchild, rchild;
}HTNode, *HuffmanTree;
|
构造算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| bool Build(HuffmanTree &HT,int * w,int n)
{
if(n < 1)
return false;
int m = 2 * n - 1;
HT = (HuffmanTree)malloc(m * sizeof(HTNode));
if(!HT)
return false;
for(int i = 0; i < n; i++)
{
HT[i].weight = w[i];
HT[i].parent = -1;
HT[i].lchild = -1;
HT[i].rchild = -1;
}
for(int i = n; i <= m; i++)
{
HT[i].weight = -1;
HT[i].parent = -1;
HT[i].lchild = -1;
HT[i].rchild = -1;
}
for(int i = n;i<m;i++)
{
int s1,s2;
Select(HT,i,s1,s2);
HT[s1].parent = i,HT[s2].parent = i;
HT[i].lchild = s1,HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
return true;
}
|
其中 select 函数的功能是从0~(i-1)的下标中选择两个权重最小的数,并返回他们的下标。
实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| bool Select(HuffmanTree &HT,int n,int &s1,int &s2)
{
int m = 0;
for(int i = 0; i < n; i++)
{
if(HT[i].parent == -1)
{
m = i;
break;
}
}
for(int i = 0; i < n; i++)
{
if(HT[i].parent == -1 && HT[i].weight < HT[m].weight)
m = i;
}
s1 = m;
for(int i = 0; i < n; i++)
{
if(HT[i].parent == -1 && i != s1)
{
m = i;
break;
}
}
for(int i = 0;i < n;i++)
{
if(HT[i].parent == -1 && i != s1 && HT[i].weight < HT[m].weight)
m = i;
}
s2 = m;
return true;
}
|
赫夫曼数的应用——赫夫曼编码
在远程通信的过程中,将出现频率高的字符用更短的编码,出现频率低的字符用更长的编码,这样就可以大幅节省传输编码的总长度。赫夫曼数正好符合这样的编码规则。
前缀编码
前缀编码(Prefix Coding)是一种编码方式,其中每个编码符号(或编码单元)都不是任何其他编码符号的前缀。这种编码方式确保了解码过程是唯一的和无二义性的,因为没有一个编码符号会与另一个编码符号的前缀相匹配。
通过赫夫曼数编码
在将需要编码的内容创建对应的赫夫曼数后,我们规定从根结点开始,向左走一步生成一个0,向右走一步生成一个1,从根结点到叶子结点的路劲即为对应内容的赫夫曼编码。
译码
译码时,遇到0就向左走一步,遇到1就向右走一步,一旦到达一个叶子结点,就译出一个内容。
构造赫夫曼编码表
步骤:
- 分配HC线性表的空间
- 分配cd空间(大小为n),置cd[n-1] = ‘\0’
- 依次求叶子结点的编码,i= 1,……,n
- 从初始值start = n-1
c = i
f = HT[i].parent
- c,f循环上找直到根结点,如果c是f 的左结点cd[–start] = 0,c是f的右结点cd[–start] = 1;
- 为第 i 个字节申请 n- start 的空间,并cd 复制给HC[i]
- 释放cd空间
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void HuffmanCoding(HuffmanTree &HT,int n,HuffmanCode &HC)
{
HC = (HuffmanCode)malloc((n + 1) * sizeof(char *));
char * cd = (char *)malloc(n * sizeof(char));
cd[n - 1] = '\0';
for(int i = 0; i < n; i++)
{
int start = n - 1;
int c = i;
int f = HT[i].parent;
while(c != 2*n-2)
{
--start;
if(HT[f].lchild == c)
cd[start] = '0';
else
cd[start] = '1';
c = f;
f = HT[f].parent;
}
HC[i] = (char *)malloc((n - start) * sizeof(char));
strcpy(HC[i],&cd[start]);
}
free(cd);
}
|
线索二叉树
线索二叉树(Threaded Binary Tree)是一种特殊的二叉树,它通过在空的左子指针和右子指针中存储指向前驱和后继节点的指针来实现中序遍历的高效性。这样可以避免在遍历过程中频繁地回溯父节点,从而提高遍历效率。(n个结点的二叉树含有n+1空指针域)
中序线索二叉树
中序线索二叉树利用结点中的空指针进行线索化,对于左孩子,让它指向该节点的前驱结点,对于右孩子,让它指向该节点的后继结点。并且通过tag标签进行标记,让我们知道哪些指针是线索指针。线索化时,我们只针对那些原本为空的指针进行线索化,并不会改变原本二叉树的结构。
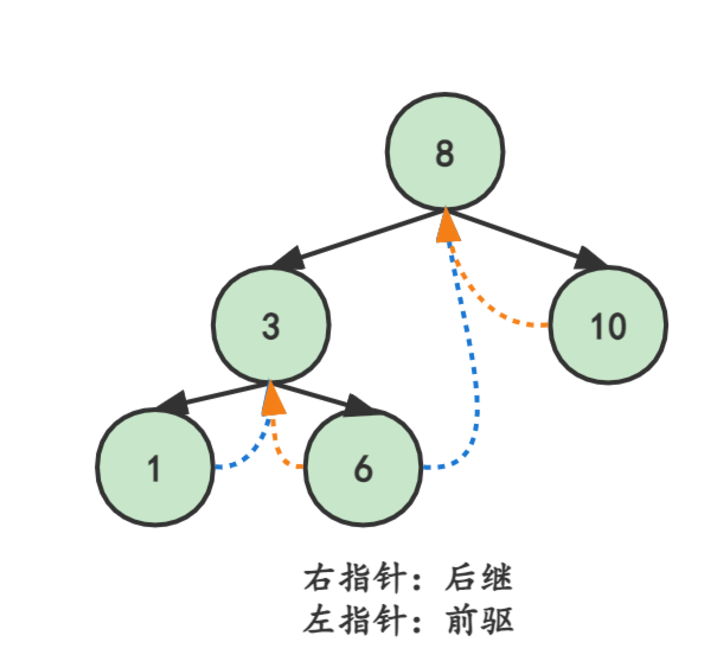
线索二叉树的结构
1
2
3
4
5
| typedef struct BiThrNode {
TElemType data;
Struct BiThrNode *lchild, *rchild;
bool LTag, RTag;
}BiThrNode, *BiThrTree;
|
中序二叉树线索化
我们先再来看一下中序遍历的代码:
1
2
3
4
5
6
7
8
9
10
11
| bool InOrderTraverse(BiTree T)
{
if(T==NULL) return true;
else
{
InOrderTraverse(T->lchild);
cout<<T->data;
InOrderTraverse(T->rchild);
return true;
}
}
|
对于中序二叉树线索化,我们只需要在中序遍历的代码上添加一点内容即可:
- 每次处理完一个结点,我们将当前结点记作下一个结点的前驱结点
- 当前结点左结点为空结点时,令左结点指向前驱结点
- 当前驱结点右结点为空结点时,令前驱结点的右结点为当前结点
ok,现在我们来看看二叉树中序化的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| BiThrTree pre = nullptr;
void InThreading( BiThrTree p)
{
if (p == nullptr) return;
else
{
InThreading(p->lchild);
if (p->lchild == nullptr)
{
p->LTag = true;
p->lchild = pre;
}
if (pre->rchild == nullptr)
{
pre->RTag = true;
pre->rchild = p;
}
pre=p;
InThreading(p->rchild);
}
}
|
与遍历的打印相似,对于当前结点的处理,仍然在处理左结点和右节点之间的位置。
中序线索二叉树遍历
对于中序线索二叉树的遍历,我们遵循以下步骤:
- 从根结点先一直向左找,找到最左孩子,既lTag == 1 或 ,lchild == nullptr。
- 从该结点开始向右遍历,如果Rtag = 1 那么就可以一直向右遍历,直到找到Rtag = 0的结点,遍历该结点后停止。
- 从我们找到的第一个Rtag = 0的结点的右结点开始,以此结点为根结点,重新开始步骤1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
ThreadedNode* findFirst(ThreadedNode* root) {
while (root->lTag == 0) {
root = root->left;
}
return root;
}
ThreadedNode* findNext(ThreadedNode* node) {
if (node->rTag == 1 || node->rchild == nullptr) {
return node->right;
}
return findFirst(node->right);
}
void inOrderTraversal(ThreadedNode* root) {
ThreadedNode* node = findFirst(root);
while (node != NULL) {
printf("%d ", node->data);
node = findNext(node);
}
}
|
树和森林
树到二叉树的转化
所有树都可以在等价的转化为一棵二叉树,其方法是,将树中的兄弟结点放在二叉树中对应结点的右子结点上,将孩子结点放在左子结点上。
转化前后如下图所示:
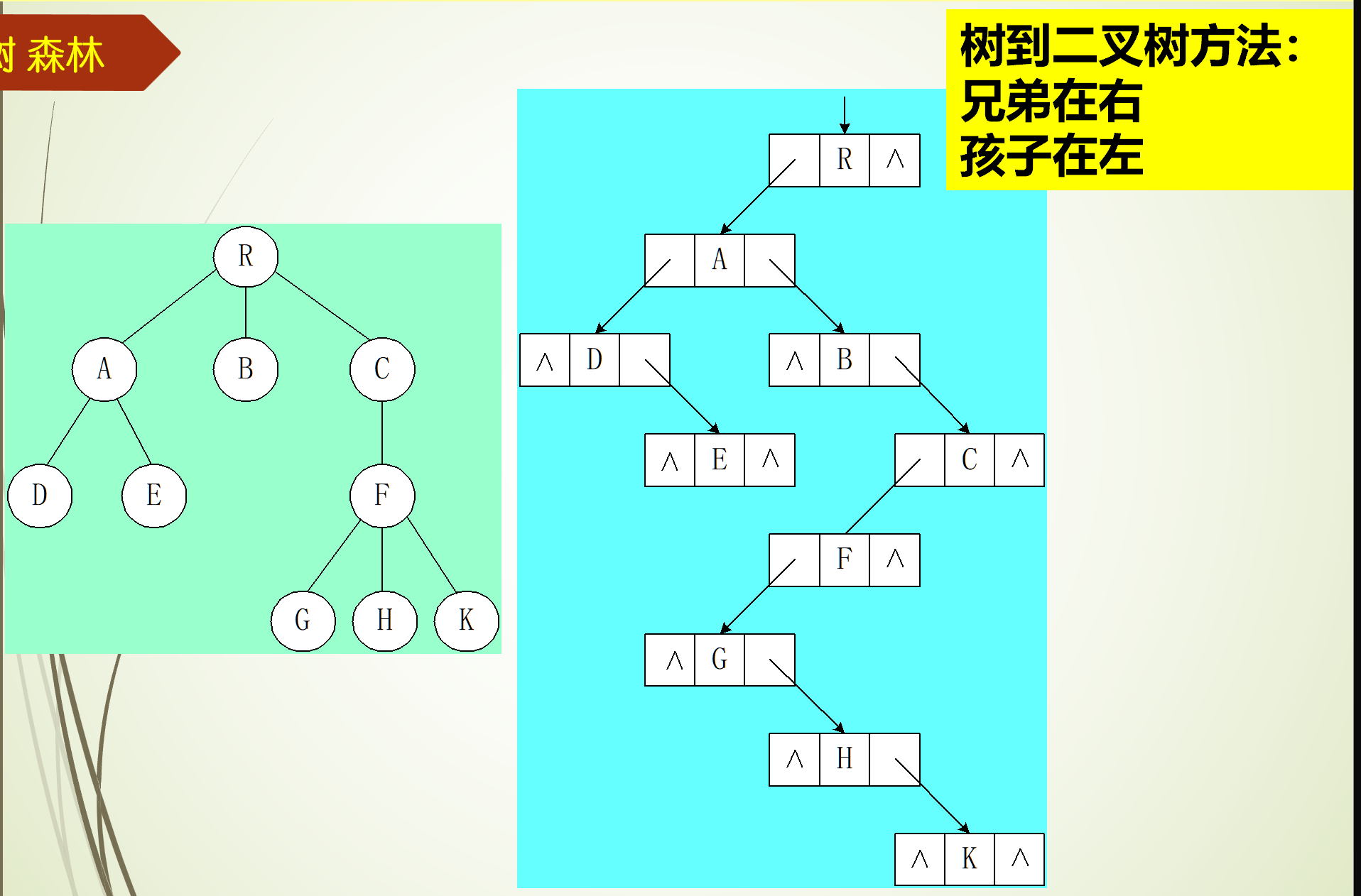
转化算法
- 在兄弟间加一连线
- 对每一个结点,去除其与所有孩子的连线,最左边的孩子除外
- 以根为轴心将整棵树顺时针转45°
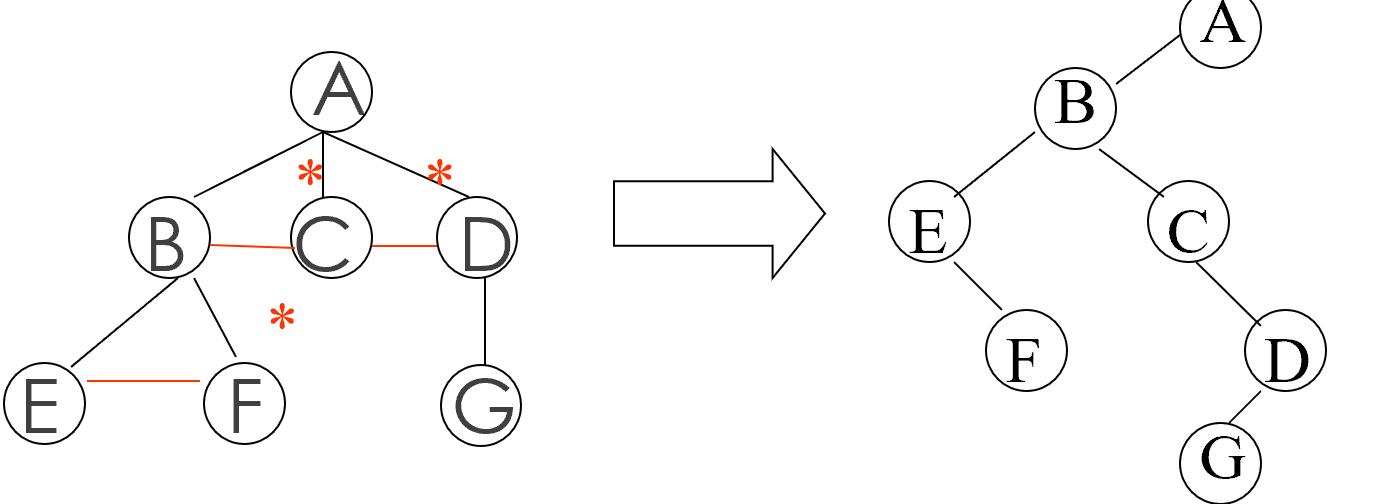
树的遍历
- 树的先根序遍历->二叉树的先序遍历
- 树的后根序遍历->二叉树的中序遍历
- 树的层序遍历->自上而下自左至右访问树中每个结点
森林到二叉树的转化
- 向将森林里的每一棵树转化成一颗二叉树
- 从最后一棵树开始,把后一颗树当作前一棵树根的右子树
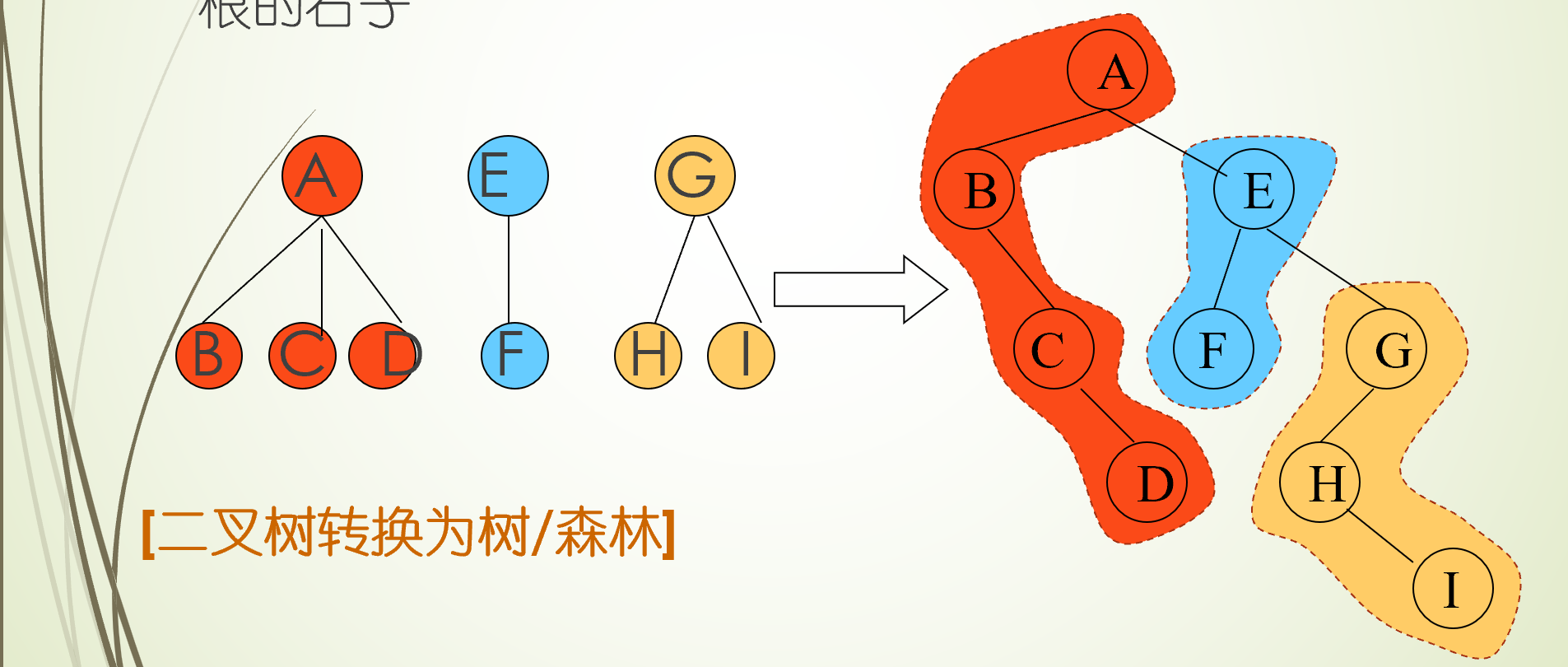
森林的遍历
- 逐棵先序遍历每棵子树->二叉树的先序遍历
- 逐棵后序遍历每棵子树->二叉树的中序遍历
树的存储结构
多重链表表示方法
1
2
3
4
5
6
| #define TREE_DEGREE 100
typedef struct MultiTNode {
TElemType data;
struct MultiTNode * ptr[TREE_DEGREE]
}MultiTNode, * MultiTree;
|
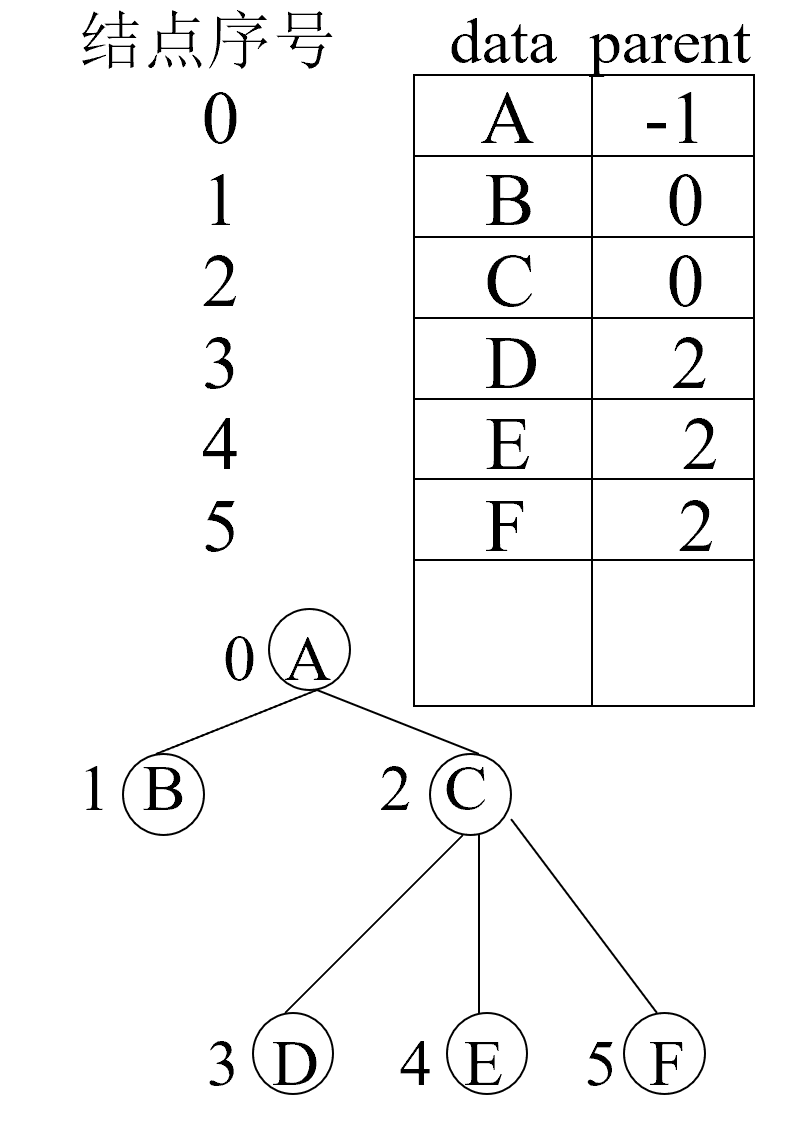
双亲表示法
用顺序存储(一维数组)存储树的信息。
1
2
3
4
5
6
7
8
9
10
| #define MAX_TREE_SIZE 100
typedef struct PTNode{
TElemType data;
int parent;
}PTNode;
typedef struct {
PTNode nodes[MAX_TREE_SIZE];
int r, n;
}PTree;
|
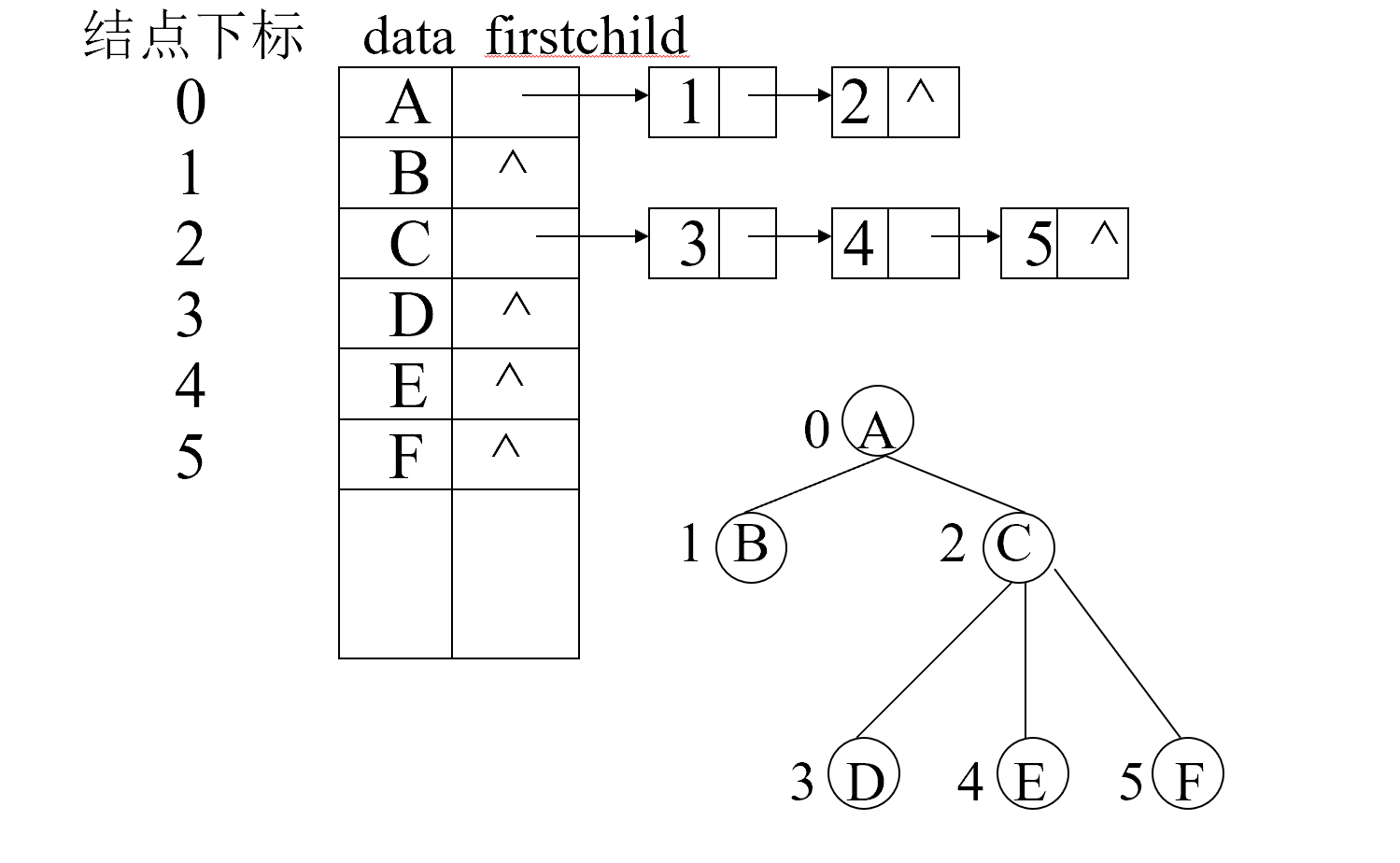
孩子链表表示法
顺序(一维数组)+单链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| #define MAX_TREE_SIZE 100
typedef struct CTNode{
int child;
struct CTNode * next;
}CTNode, * ChildPtr;
typedef struct {
TElemType data;
ChildPtr firstchild;
}CTBox;
typedef struct {
CTBox nodes[MAX_TREE_SIZE];
int r, n;
}CTree;
|
所有的结点存储在一个数组中,如果该结点有孩子,那么该结点链式连接它的所有孩子(不是子树,只连接直接孩子)
孩子兄弟表示法(二叉链表表示法)
1
2
3
4
5
| typedef struct CSNode {
TElemType data;
struct CSNode *fch,*nsib;
}CSNode, * CSTree ;
|
该表示方法即为通过二叉树表示树的方法,左结点指向第一个孩子,右结点指向相邻的兄弟。





