串
定义: 零个或多个字符组成的有限序列
衍生定义:
- 子串:串中任意个连续的字符组成的子序列称为该串的子串。
- 主串:包含子串的串称为主串
- 串相等:两个串长度相等,且对应位置的字符都相等
- 空格串/空白串:由一个或多个空格组成
- 空串:空串不包含任何字符,长度为0。
串的顺序存储结构
定长顺序存储表示
存储定义:
1
2
| #define MAXSTRLEN 255
typedef unsigned char SString[MAXSTRLEN+1];
|
在SString[0]处存放字符串的长度
约定:串值长度上溢时,用“截尾法”处理,即“截断”超过予定义长度的部分。
StrCompare()
1
2
3
4
5
6
7
8
9
| int StrCompare(SString S, SString T)
{
for(i=1; i<=S[0] && i<=T[0]; i++)
if( S[i] != T[i] )
return(S[i] - T[i] );
return S[0]-T[0]
}
|
Concat
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| bool Concat(SString &T, SString S1, SString S2)
{
if( S1[0]+S2[0] <= MAXSTRLEN ) {
T[1..S1[0]] = S1[1..S1[0]];
T[s1[0]+1..S1[0]+S2[0]] = S2[1..S2[0]];
T[0]= S1[0]+S2[0]; uncut=TRUE;
}
else if (S1[0]<MAXSTRLEN) {
T[1..S1[0]] = S1[1..S1[0]];
T[s1[0]+1..MAXSTRLEN] = S2[1..MAXSTRLEN-S1[0]];
T[0]= MAXSTRLEN; uncut=FALSE;
}
else {
T[0..MAXSTRLEN]= S1[0..MAXSTRLEN];
uncut= FALSE;
}
return uncut;
}
|
SubString
1
2
3
4
5
6
7
8
9
10
11
| Status SubString(SString &Sub, SString S, int pos, int len)
{
if( pos<1 || pos>S[0] || len<0 || len>S[0]-pos+1 )
return ERROR;
Sub[1..len]= S[pos..pos+len-1];
Sub[0]= len;
return OK;
}
|
堆分配存储表示
代码定义:
1
2
3
4
| typedef struct{
char *ch;
int length;
}HString;
|
动态分配串值存储空间,避免定长结构的截断现象。
串的块链存储结构
串的块链存储结构通过链表来实现,不过在链表中存贮时,一个节点既可以只存储一个字符也可以存储多个字符,每个节点称为块,通过改变尾指针,在进行连接操作时很方便,但是其他操作很不方便,且占用储存大,很少应用。
代码定义:
1
2
3
4
5
6
7
8
9
10
11
| #define CHUNKSIZE 4
typedef struct Chunk {
char ch[CHUNKSIZE];
struct Chunk * next;
}Chunk;
typedef struct {
Chunk * head, * tail;
int curlen;
}LString;
|
BF匹配算法
先导:在这一节中,我们将需要寻找的字符串叫做模式串,即我们需要在主串中寻找是否由模式串存在。
暴力穷举法,从主串的第0个字符开始比较,用i跟踪,和匹配字符串的第一个字符(用j跟踪)比较,若相等,则继续比较后续的字符;若不等,从主串的下一字符起,从主串的下一字符起(i=i-j+2),重新与模式的第一个字符(j=1)比较。直到主串的一个连续子串字符序列与模式相等 。返回值为S中与T匹配的子序列第一个字符的序号,即匹配成功。否则,匹配失败,返回值 0。否则,匹配失败,返回值 0
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| bool Index(char* s,char* p,int * pos)
{
for(int i = 0;s[i] != '\0';i++)
{
int j = 0,ti = i;
if(s[ti] == p[j])
{
while(p[j] != '\0' && s[ti] != '\0' && p[j] == s[ti])
{
ti++,j++;
}
if(p[j] == '\0')
{
*pos = i;
return true;
}
}
}
return false;
}
|
BF算法的时间复杂度为最好情况为O(n*m)。所以我们来了解一种效率更高的匹配算法。
KMP算法
想要更好的理解KMP算法,我们需要先引入KMP算法中的next数组概念
next数组
next数组的长度与模式串相等,其中存放的数据类型为整型。我们先举个例子来看一下什么是next串。
1
2
3
| 位置 :0 1 2 3 4 5
字符串:A B A B A C
next : 0 0 1 2 3 0
|
乍一看可能看不出来什么规律,我们一个一个来看一下,我们先看第一个非零数字1,它在第2个位置。它指的是,在前3个字母组成的字符串中,前1个字母和后1个字母相同。
在来看处在第4个位置上的数字2,它的意思就表示前4个字母组成的字符串中前2个字母与后2个字母相同。
那么第5个位置的3即为前5个字母组成的字符串中前3个字母与后3个字母相同。
0的位置都表示前 i 个位置上首尾都不相同。
KMP算法匹配模式
知道了next数组,我们就可以来学习KMP算法的匹配模式。
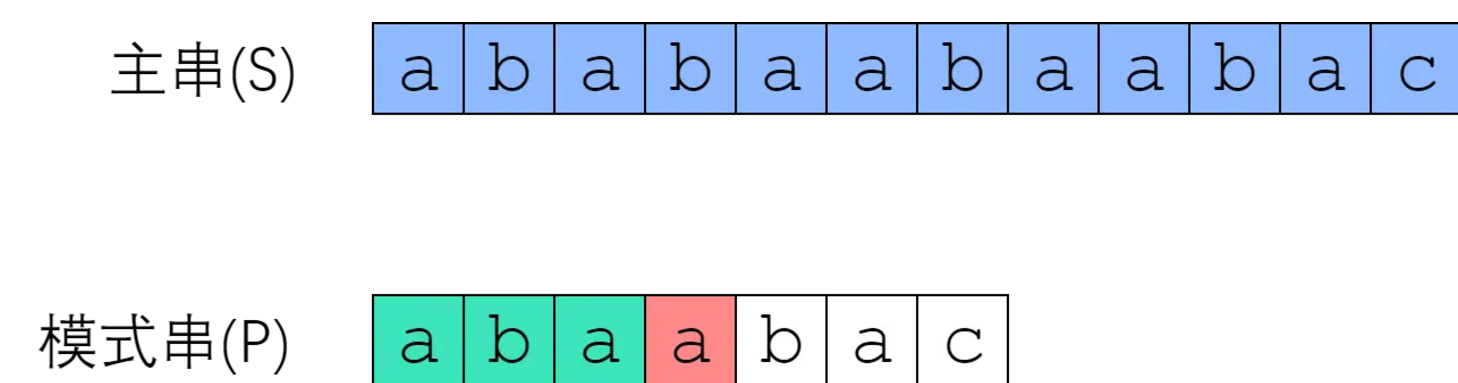
当P串与S串匹配到第4个字符时,出现了失配,若是按照BF算法,此时我们应该从 i= 1,j = 0 的地方从新开始匹配,但是这样的化,我们以及完成匹配的字符的就需要重新匹配一遍,我们仔细查看两个字符串,虽然第4个位置失配,但是第1个位置与第3个位置的字符相同,即next[2] = 1,我们可以直接保持i不变,令 j = 1,继续开始匹配。
就变成下面这样:
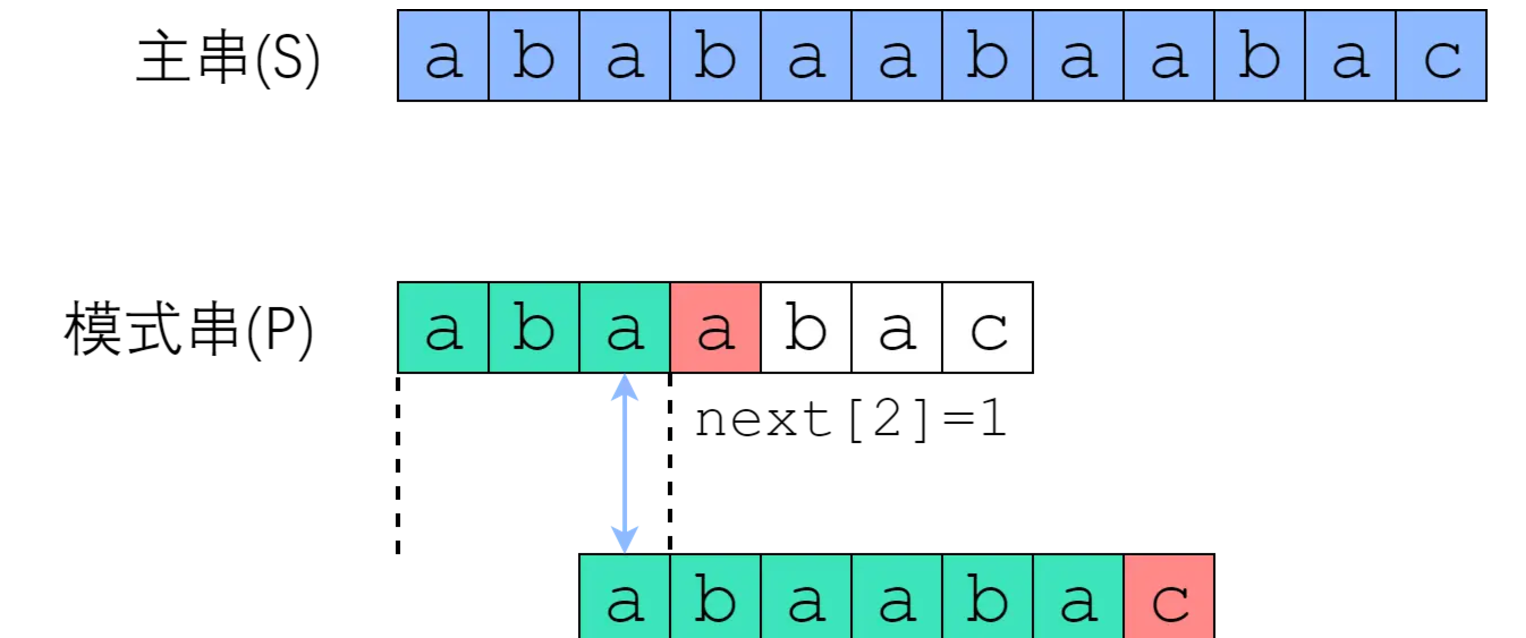
此时第7个位置又发生失配,但是next[5] = 3 ,则我们可以保持i不变,令:j = 3,继续匹配。
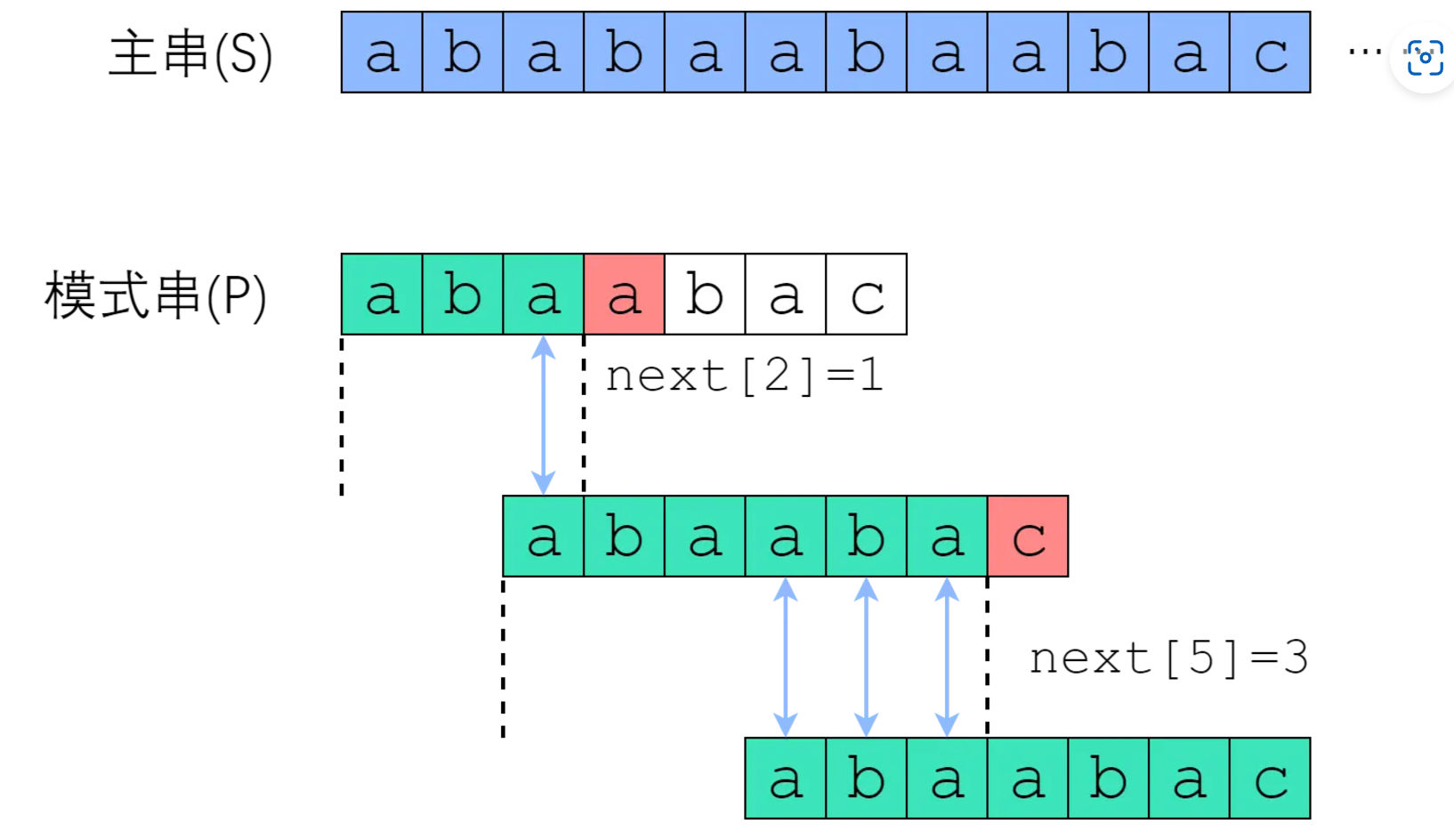
我们总结一下算法:
- 匹配过程中,i ++,j++。
- 若是遇到失配,则令j = next[j],然后继续匹配。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| bool IntIndex_KMP (char* s,char* p,int* pos,int* next)
{
int i= 0; int j = 0;
while(i<strlen(s) && j<strlen(p))
{
if(s[i]==p[j])
{
i++,j++;
}
else{
while(j>0 && s[i]!=p[j])
{
j=next[j-1];
}
if(s[i]!=p[j])
{
i++;
}
}
}
if (j == strlen(p))
{
*pos = i - strlen(p);
return true;
}
else{
pos = NULL;
return false;
}
}
|
next数组实现
现在我们只需要学会如何计算next数组。
在计算next数组时,我们运用两种思想,一种是递推,一种是KMP匹配算法,没错,在计算next数组时,我们仍然用到了KMP匹配的思想。
首先在只有一个字母时,我们规定next[0] = 0。
接下来,我们根据这一点开始递推,递推规则如下:(设置两个变量,j = 0,i = 1))
- p[i] == p[j] ,next[i] = ++j
- p[i] != p[j], 令 j = next[j-1]
- if j == 0, next[i] = 0
我们发现其实第2条与KMP匹配的代码非常相似
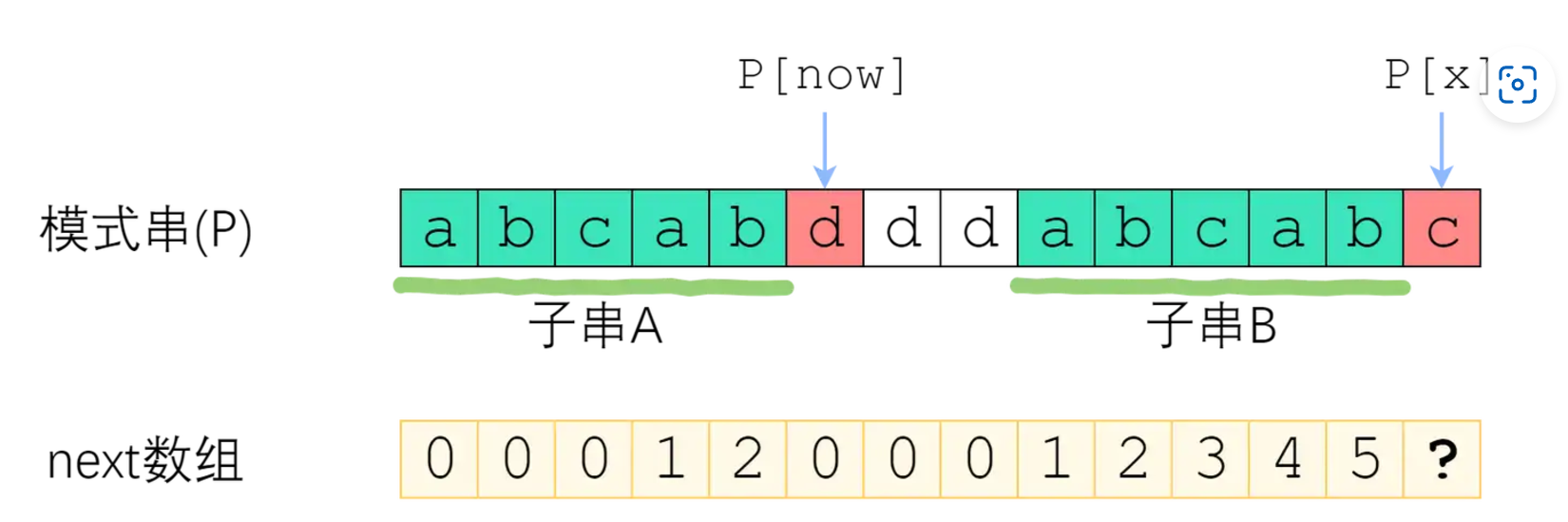
对于这个P,当d 与c失配时,我们从next[now-1]得知,尾部的ab与开头的两个字母相等,所以令now = next[now-1] 则我们可以直接跳跃到下一个能够匹配c前面ab的地方,再检查第3个字符是否相等即可。
计算next数组代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| int* get_next(char* p,int* mn)
{
size_t m = -1;
for(m = 0;p[m]!= '\0';m++);
*mn = m;
int* next = (int*)malloc(sizeof(int)*m);
next[0] = 0;
int i = 1,j = 0;
while(i<m)
{
if(p[i] == p[j])
{
j++;
next[i++] = j;
}
else
{
if (j == 0)
next[i++] = 0;
else
j = next[j-1];
}
}
return next;
}
|
在0下边存放串的长度
在0下标存放数组的长度,我们让p与next 的下标对其,next[0] = 0,next[1] = 0。那么我们原来的next数组需要全体右移一位,并且每一位+1。然后我们舍去最后一位的值,并集给第一个值的next值标记为0:

则此时next计算代码改为如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| int* get_next(char* p)
{
int* next = (int*)malloc(sizeof(int)*p[0]);
next[0] = 0,next[1] = 0;
int i = 1,j = 0;
while(i<p[0])
{
if(j == 0 ||p[i] == p[j])
{
i++,j++;
next[i] = j;
}
else
{
j = next[j];
}
}
return next;
}
|
计算nextval 的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| int* get_nextval(char* p)
{
int* next = (int*)malloc(sizeof(int)*p[0]);
next[0] = 0,next[1] = 0;
int i = 1,j = 0;
while(i<p[0])
{
if(j == 0 ||p[i] == p[j])
{
i++,j++;
if(p[i] != p[j])
next[i] = j;
else
next[i] = next[j];
}
else
{
j = next[j];
}
}
return next;
}
|
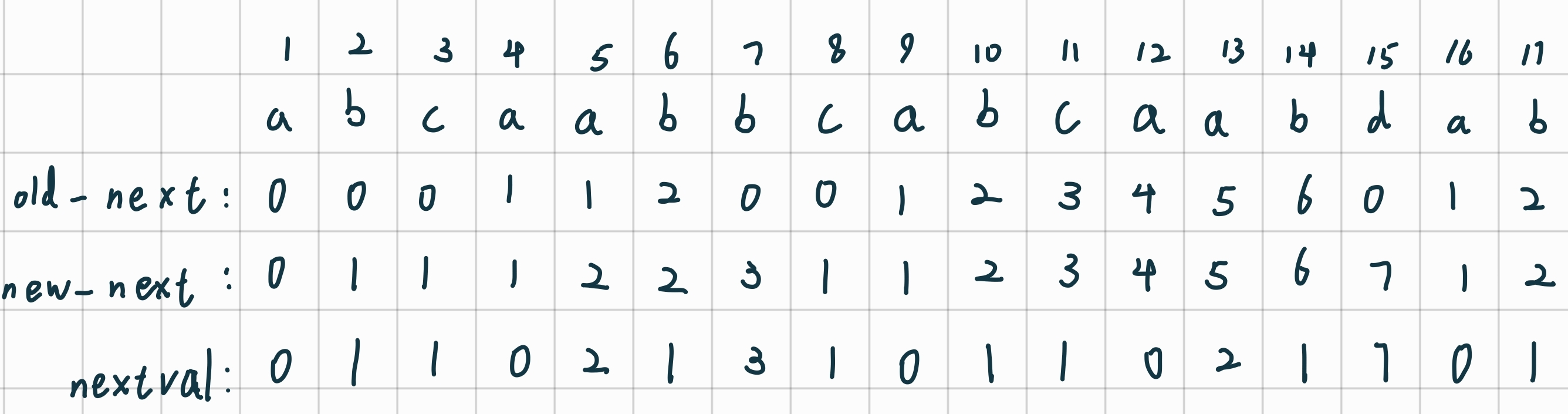
示例:
计算nextcal的思想主要是:
- 在next数组中挨个遍历,如果a[i] == a[next[i]],则让nextval中nextval[i] = nextval[next[i]]
此时kmp算法代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| bool IntIndex_KMP (char* s,char* p,int* pos,int* nextval)
{
int i= 1; int j =1;
while(i<=s[0] && j<=p[0])
{
if(j==0 || s[i]==p[j])
i++;j++;
else
j=nextval[j];
}
if (j>p[0])
{
*pos = i-p[0];
return true;
}
else
return false;
}
|





