计算机系统基础第二章_信息的表示和处理

计算机中信息的表示

计算机中的所有信息都通过0和1表示，同时大多数计算机使用8位的块，也就是1个字节，作为最小的可寻址单位，这也就是说计算机中一个最小地址单位中包含8个bit位。

进制转换

二进制表示法太冗长，为了简化二进制位的表示，我们通常用8进制和16进制数来表示二进制位，这样既能简短表示长度，同时也方便与二进制位进行转化。在16进制中我们将‘A’’B’ ‘C’ ‘D’ ‘E’ ‘F’用来表示数字10，11，12，13，14，15。

一个8进制位能表示3个二进制位，一个16进制位能表示4个二进制位，这意味着一个字节的内容仅需一个2位的16进制数就能表示。

并且每个位的数字直接转为2进制位再拼接起来，就方便的得到2进制位。

在c语言中 0x开头表示的数字一般被认为是16进制数，如 0xFFFFFFFF就表示一个32位二进制数，且每个位都是1。

再来看一个例子：0x173a4c(16进制数的字母即可大写也可小写)

再把二进制数拼接起来，我们就得到了 0x173a4c的二进制表示： 000101110011101001001100

同样对于二进制转16进制数：

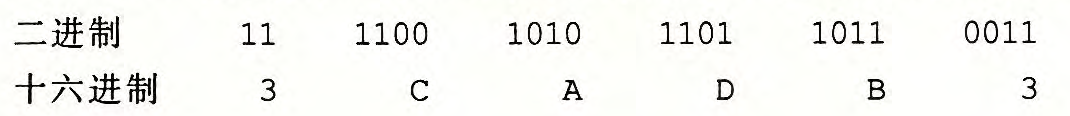
如果高位不满4位，我们可在其高位补0，11即为 0011所以是3。

字数据大小

字长

对于手机或者电脑程序有了解的朋友可能听说过32位程序或者64位程序这样的字眼，这里的32位和64位表示的是计算机的字长(word size)，用来指明指针数据的标称大小(nominal size)。光是这样定义可能还是无法理解。其实，这里的字长的大小决定了程序能够访问的虚拟地址空间的最大大小，对于32位的机器来说，虚拟地址的范围是0~2^32-1，一个程序能访问的最大内存大小就是4GB。而64位的机器则为16EB，这根本并不是一个数量级。

寻址和字节顺序

在计算机中，很多对象占的空间往往大于一个字节，例如int，double等，那么就涉及到这个对象的地址是什么，以及如何在内存中排列他们两个问题。

对于问题1：对象的地址是什么？

对于几乎所有计算机，占用多个字节的对象的数据都在内存中连续存储，我们选取所使用字节中最小的地址作为这个对象的地址。

对于问题2：如何在内存中排列他们？

计算机界有两种常用的不同的做法。大端法和小端法。

大端

机器按照从最高有效字节到最低有效字节的顺序存储

也就是将数据的低位存储在较大的地址上，将数据的高位存储在较小的地址上

我们来看一个二进制数 Ox01234567，7是这个数字的最低位，0是这个数字的最高位。我们习惯，将高位写在左侧，低位写在右侧。

而在书写内存地址时，我们通常将低位写在左侧，高位写在右侧。

大端法将最高位写在最小地址，最低位写在最大地址，虽然在内存中的顺序是倒过来的，但是在人的眼中却符合我们平时阅读数字的习惯。

小端

机器选择在内存中按照从最低有效字节到最高有效字节的顺序存储对象

小端把数据的低位存在地址的低位，数据的高位存在地址的高位。

需要注意的是，这里大端小端的存储方法，并不影响一个字节内部8个位的排序方式。

c语言中的位级运算

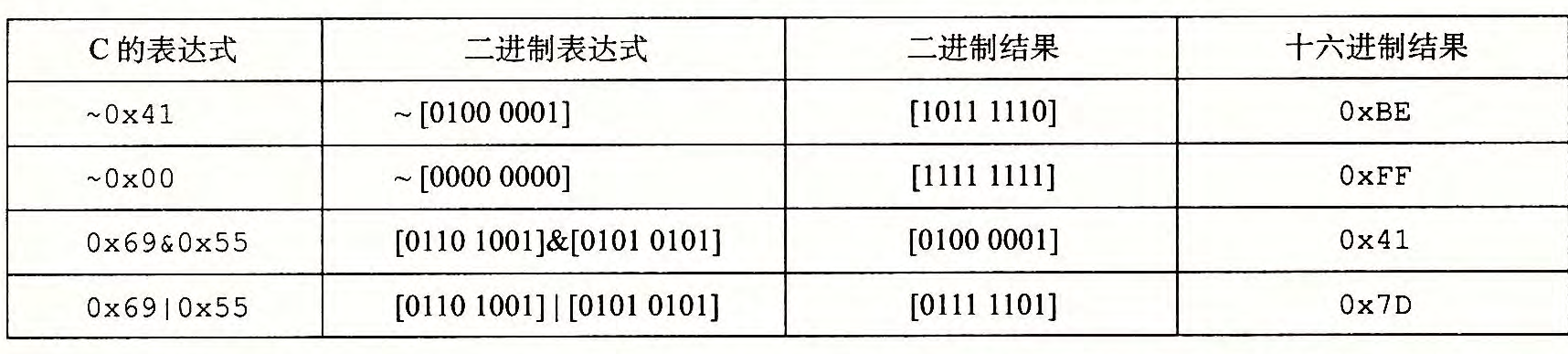
基本逻辑运算

按位与：&

按位或：|

取反：~

异或：^

掩码运算

掩码运算可以将一段二进制数据中的其他位全部抹零，只保留选择部分的数据的信息。就好像把其他信息用黑布遮住，只让你看到你想看的那一段的数据。

具体操作如下：

对于 x= 0x89ABCDAB，我们只想要获取最后两个16进制位的数据。

我们让x进行如下操作：

x & 0x000000FF

对于想要保留的信息，我们让他 与1，想要遮住的信息，让他 与0。我们就得到：0x000000AB

位移运算

位移运算是吧数据的二进制位向左或向右移动k位，新增的数据用0补齐，超位的数据溢出，也可理解为是对数据进行乘或除以2的k次幂。

左移：<<

右移：>>

其中右移有两种移动方式：逻辑右移和算数右移

其区别是，逻辑右移在右侧补0，而算数右移在最高位补原本最高位的数据，例如 10000001，我们将其算数右移两位，则得到 11100000，而逻辑右移则为：00100000.

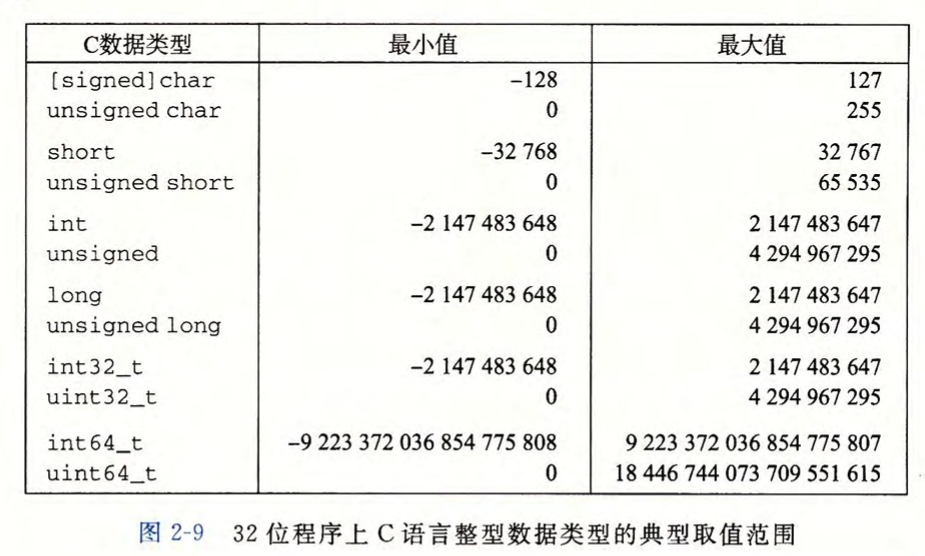
整数表示

c语言中有很多可以表示整数的类型常见类型及其范围如下：

无符号数的编码

对于一个w位的整数类型，其能够表示的范围为：0~$2^w-1$，每个整数对应的编码就是这个数据的二进制编码，例如11的二进制表示为：1011。缺的位在数据前面补0.

无符号数的机器码计算10进制数的公式为：

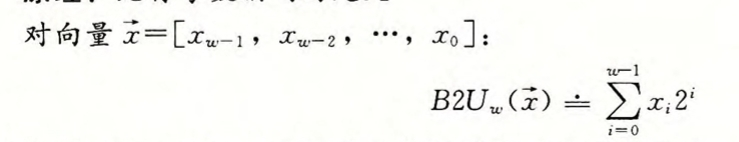
补码编码(two’s-complement)

补码编码常常在计算机中表示负数，我们将字的最高有效位解释为负权(negative weight)。

计算公式为：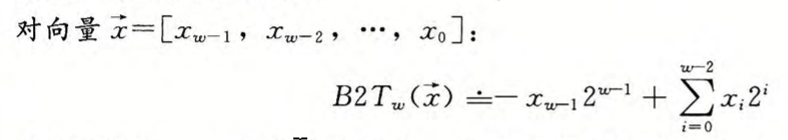

最高位负权我们也常常称为符号位用来表示这个数字是正数还是负数，只有为负数时符号位才为1。

通过定义，我们发现对于w位的类型，能够表达的最小值为 $-2^{w-1}$ ,但是对于最大值为：$2^{w-1}-1$,负数的绝对值为正数+1。

补码转原码

1. 检查最高位（符号位）：
   • 如果符号位是0，表示这是一个正数，补码和原码相同。
   • 如果符号位是1，表示这是一个负数，需要进行转换。
2. 对于负数：
   • 将补码取反（除符号位的所有位取反）。
   • 取反后的结果加1，得到原码。

原码转补码

1. 检查最高位（符号位）：
   • 如果符号位是0，表示这是一个正数，原码和补码相同。
   • 如果符号位是1，表示这是一个负数，需要进行转换。
2. 对于负数：
   • 将原码取反（除符号位的所有位取反）。
   • 取反后的结果加1，得到补码。

有符号数和无符号数之间的转换

c语言允许各种不同的类型相互转化，比如 ：

short int v = -12345;
unsigned short uv = (unsigned short) v; 
printf("v = %d, uv = %u\n", v, uv);

得到结果如下：

V = -12345, UV= 53191 

这两个数据的二进制表示完全相同，我们可以发现，在c程序中进行强制类型转换，程序并不会改变位值，只是改变了解释这些位的方式。

对于大多数C语言的实现，处理同样字长的有符号数和无符号数之间相互转换的一般规
则是：数值可能会改变，但是位模式不变。

同时我们可以发现有以下规律：

12345 + 53191 = 65 536 = 2^16 

所以我们得到如下公式：

对于正数：

x = ux

对于w位的数据类型，其有符号类型和无符号类型的转化公式如下(负数)：x<0

x = ux - 2^w
ux = 2^w + x

C 语言中的有符号数与无符号数

在c语言中，声明一个数据时，默认是作为有符号数来存储，若要声明一个无符号数必须加上后缀字符 ‘u’ 或者 ‘U’，例如， 12345U 或者 0x1A2Bu。

对于print函数，占位符：”%d” “%u” “%x” 分别来表示十进制有符号数，十进制无符号数，16进制数。

在c语言中，若想便捷的表示各个类型变量的MAX和MIN值，可以引用 #include<limits.h>

其中定义了许多类似如下的常变量：

扩展一个数字的位表示

想要将一个较小类型的变量扩展为一个更大的数据类型，就是这节的内容，但是在进行扩位的时候，针对无符号数和补码编码方式有不同的方法。其扩位方法类似于逻辑右移和算数右移的思想。

1. unsigned 类型

   要将一个无符号数转换为一个更大的数据类型，我们只要简单地在表示的开头添加0。这种运算被称为零扩展(zero extension) 。

2. 补码

   补码数字转换为一个更大的数据类型，可以执行一个符号扩展(sign extension), 在表示中添加最高有效位的值。

这里我们可能需要注意一点，在16位的数据中，-12345和53191二进制位相同，但是如果扩位到32位，那么他们 的二进制数则不再相同。

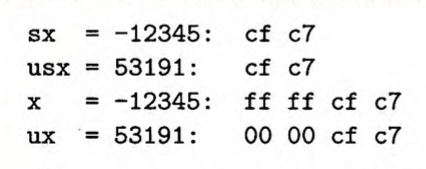
此时二进制位相同的有符号数和无符号数应该满足新的位的规则即：(x<0)

$| x | + ux = 2^{32}$

截断数字

假设我们不用额外的位来扩展一个数值，而是减少表示一个数字的位数。例如下面代码中这种情况：

int x = 53191; 
short sx = (short) x; // -12345
int y = sx; // -12345

将32 位的 x 赋值给 16位的short sx时，我们将x的前16位进行截断然后赋值给了sx，此时16位的位模式就是-12 345 的补码表示，再将s进行扩位，则会在前面补1，从而生成-12345 的 32 位补码表示。

1. 截断无符号数

   

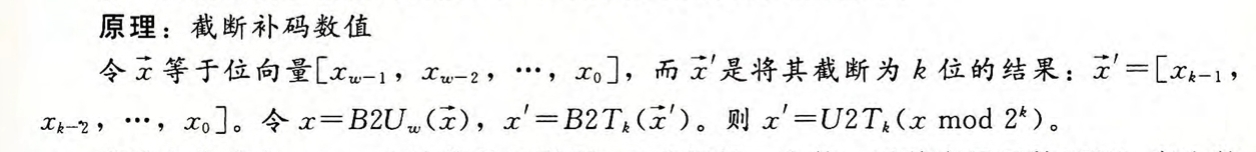
   截断一个无符号数只保留了这个数据的前k个二进制位的数据，其得到的结果与 x mod 2^k是一致的

2. 截断补码

   

   看书上的定义些许晦涩难懂，总结一下，其实就是以下步骤：

   1. 把有符号数的二进制编码以一个无符号数的方式转为10进制
   2. 用无符号数的截断规则进行截断即 x mod 2^k
   3. 将截断后的数据转成k位的有符号数

整数运算

无符号加法

对于无符号数的加法，我们可以进行如下定义：

假设有两个无符号数x, y，他们的数据类型有w个二进制位，则有：

x + y = (x+y) mod 2^w

当x + y < 2^w时，结果就为：x + y；但是当x+y在二进制上产生进位，并且这个进位产生溢出时，我们仅仅保留了数据的2^w位，相当于对于数据进行了取模运算，只保留了低位的数据。

我们再来了解一下书上定义的运算：

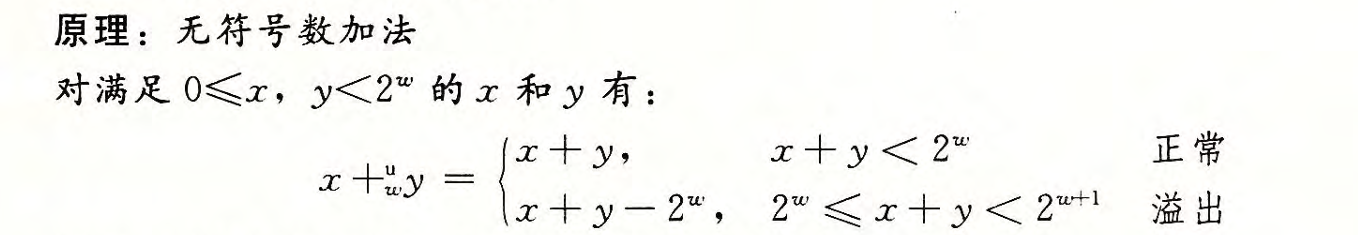
那么我们如何检测x+y是否产生了溢出现象呢？

补码加法

首先我们定义补码加法，与定义无符号加法类似，只不过将u换为了t。

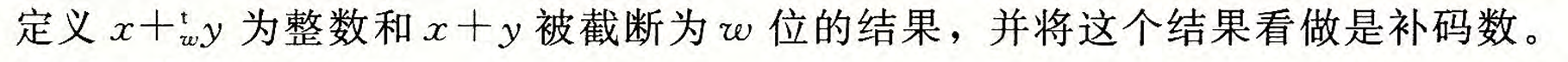
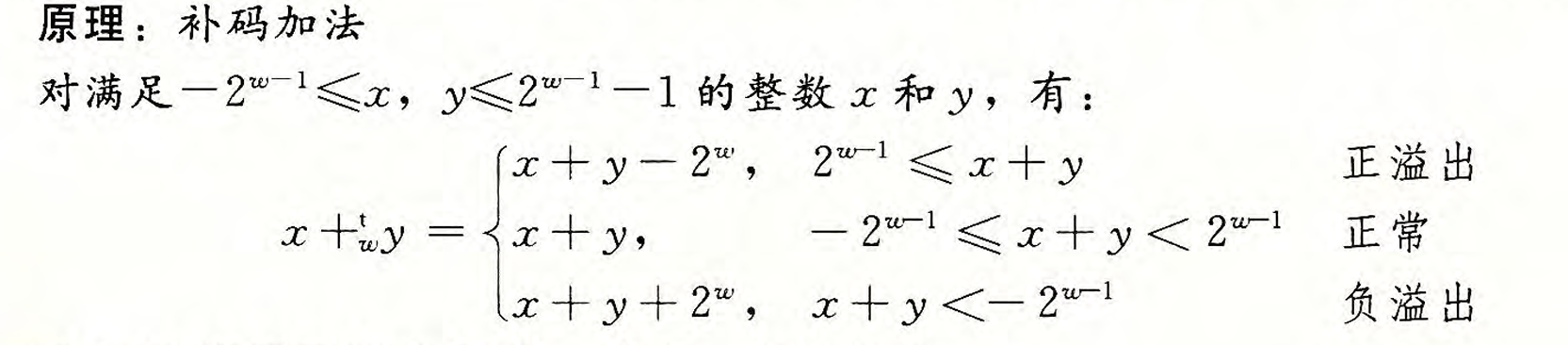
这里我们解释一下当 $x + y \geq 2^{w-1}$ 的情况和 $x + y < -2^{w-1}$ 的情况。

正溢出

对于正溢出的情况我们可以先将其视为无符号数的加法来看待，当 x+y >= $2^{w-1}$时最高位符号位变为1，也就是最高位负权为1。

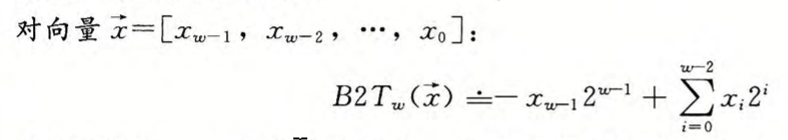
根据补码的编码规则，那么 $x + y = ((x + y) \bmod 2^{w-1} - 2^{w-1})$ 因为这里我们 $x + y \geq 2^{w-1}$,所以 $(x + y) \bmod 2^{w-1} = x + y - 2^{w-1}$

所以最后化简得到： $x + y = x + y - 2^w$

负溢出

负溢出时，我们同样先将有符号数的二进制位当作无符号数来计算，我们同样得到：$x + y = ((x + y) \bmod 2^{w-1})$ 并且当满足 $x + y < -2^{w-1}$ 时，最高位符号位变为0，

所以没有负权变为0，则此时x+y的截断的w位直接当作无符号数编码即可。所以我们根据补码转无符号数编码规则得到：$(x + y) = x + y + 2^w$

溢出检测

对于正溢出和负溢出的检测都很简单，设s = x+y:

1. 正溢出： x >0 , y>0; s<0.
2. 负溢出：x < 0 , y<0;s>0.

补码的非

我们先看定义如下：

补码的非定义为：设一个数为x，若满足：x+y = 0，则y是x补码的非。（TMinw<x,y<Tmaxw）

无符号数乘法

对于范围在 UMinw<x,y<Umaxw 的x,y。他们的范围最高可能需要2w位来表示，C语言中的无符号乘法被定义为产生w位的值，就是2w位的整数乘积的低w位表示的值

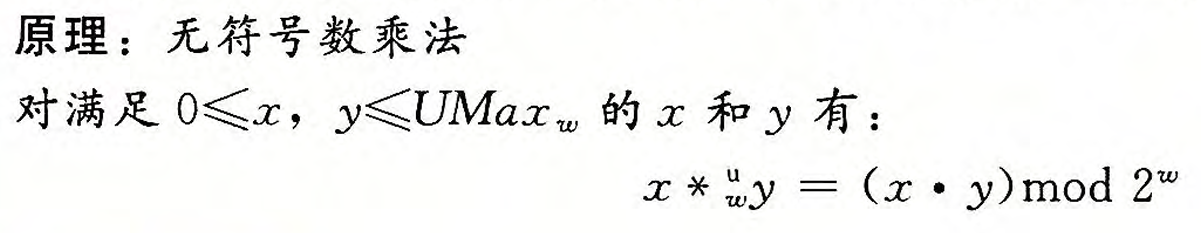
补码乘法

对于补码进行乘法，仍然最高需要2w位来表示，在c语言中，我们同样取前w位作为x*y的值。

无符号和补码乘法的位级等价性

这两种数值表示方式进行乘法操作时，结果在二进制位级上是相同的，即：二进制结果不因有符号或无符号表示的不同而变化。

所以对于无符号数和补码进行乘法时，所运用的方法和规则都是相同的，无需特殊特殊处理，只需要转化处理数据的读取方式。

乘以常数

在大多数计算机中，直接执行乘法运算会运行的相对较慢，但是有一种方法可以让我们通过加减和位移运算来代替乘法运算，我们来了解一下：

乘以 2 的幕

乘以2的幂时，我们可以直接通过位移运算来代替。

比如我们执行 x * 32时，32是2的五次方，我们可以用：x << 5 来替代。

可用2的幂次来表示的数

所有的数都可以用二进制来表示，那么所有的数都可以通过二的次幂的和相加得到，比如14 = 2^3 + 2^2 + 2^1 , 那么我们就可以将x * 14 转化为：

x * 14 = x * 8 + x * 4 + x * 1 = x<<3 + x<<2 + x<<1

编译器为了优化程序的速度，在进行程序编译时，常常进行这样的转化。

除以2的幂

在大多数机器上，整数除法要比整数乘法更慢，所以我们依然使用类似乘法的技巧来进行出发运算，只不过触发我们进行的是右移。

但是在真正来学习除法之前，我们可能需要先了解一个概念

这个定义简单的规定了两种取整方式，一种是向上取整，一种是向下取整。

无符号数的除法

在除法运算中，无法除尽是很常见的，但是int等很多类型，只能保存整数，在这个时候，我们的运算都是取整的。

对于无符号除法，我们右移运算后的结果是向下取整的。这也符合c语言乘法运算的取整方式

我们通过12340 在 16 位表示上执行逻辑右移的结果，以及对它执行除以 1、 2、 16 和 256 的结果。通过对比发现所有结果都是正确的。

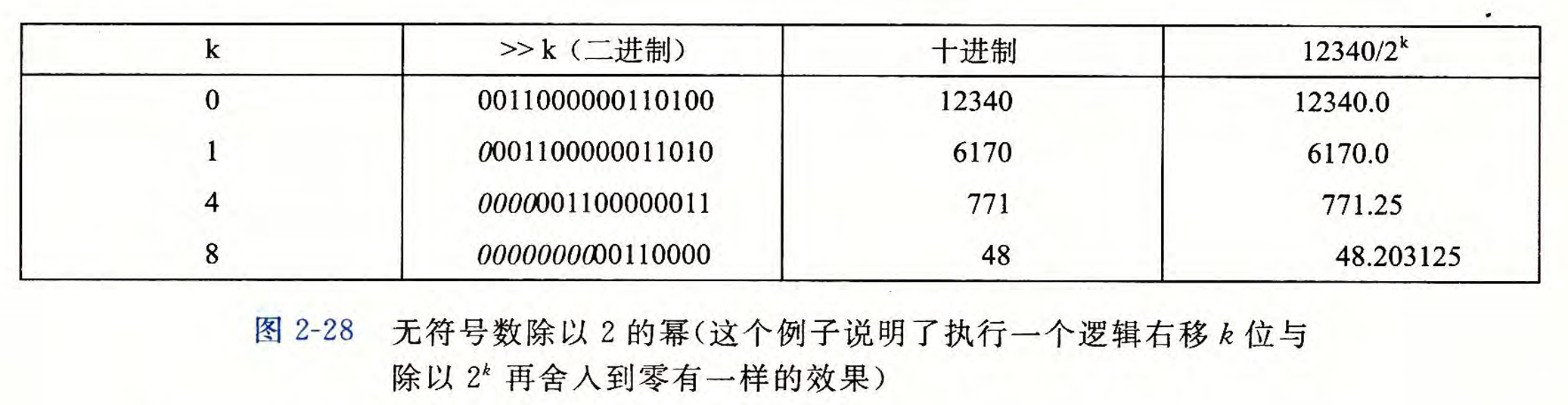
补码除法

对于正数来说，其运算与无符号数相同，我们这里不再赘述，我们重点来看一下负数除法的运算：

我们同样来看一下-12340的 16 位表示进行算术右移不同位数的结果。

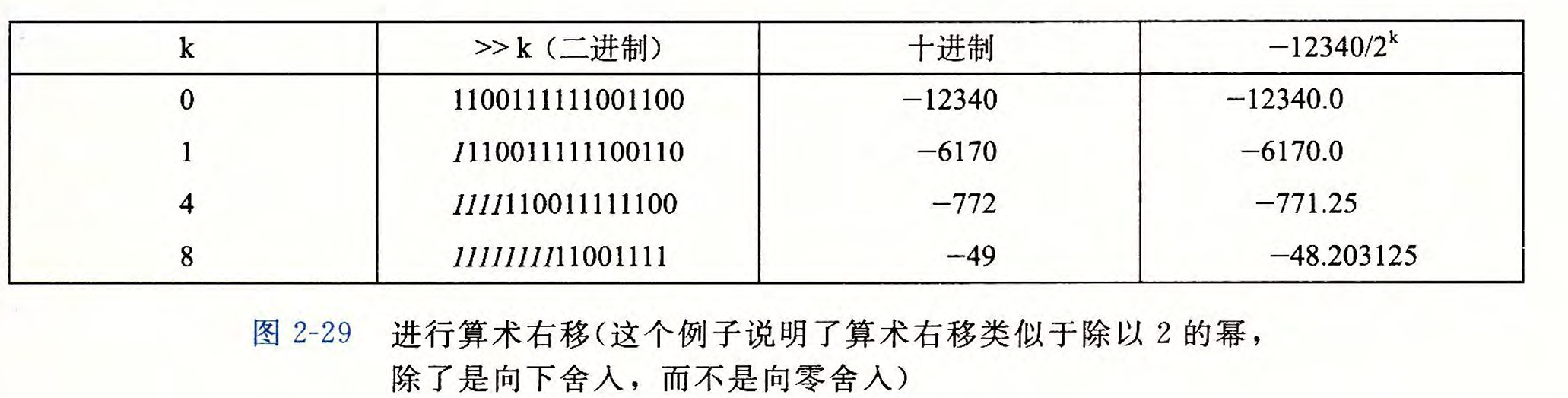
我们可以看到，通过当前的方法来进行运算，仍然是向下取整的，但是我们来看一下c语言实际输出是什么样的：

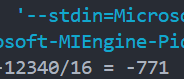
这与我们的方法取整方式产生了不同的结果，c程序在执行负数除法时是向上取整的。我们需要调整在处理负数时的除法。

这个方法就是在负数进行除法时加上一个偏量，这里的偏量是 2^k -1。

我们来看加入偏量后的效果：

浮点数

二进制小数

类似10进制对于小时的编码规则，小数点左侧是10的正幂，小数点右侧是10的负幂，我们对于2进制小数的编码规则也采用类似的方法。

同样和10进制类似，2进制也有很多小数无法精确表示，我们通过近似的方法表示，小数点后的二进制位越多，表示的越精准。

IEEE浮点表示

通过定点表示法不能表示很大的数字，我们通过IEEE浮点表示法来让浮点数既能表示很小，又能表示很大的数，因此才叫浮点数，它的小数点是不固定的。

将小数点左移1位相当于给数乘以1/2，右移1位相当于给数乘以2。所以我们通过给数字乘以一个2的幂次来控制小数点的移动。

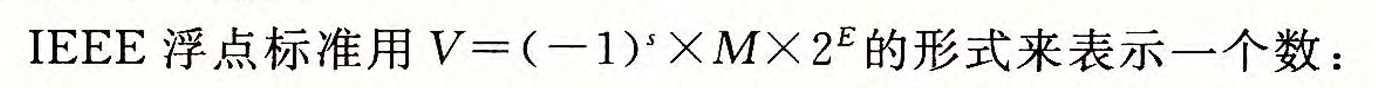
• s 符号位，用来表示正负
• 尾数(significand) M这是一个二进制小数。
• 阶码(exponent) E的作用是对小数点加权，即位移小数点

在c语言中对于单精度（float）和(double) 的编码方式如下：

• float
  • 占用4字节（32位）
  • 1个符号位
  • 8个指数位
  • 23个尾数位（隐含一个1，总共有24位）
• double
  • 占用8字节（64位）
  • 1个符号位
  • 11个指数位
  • 52个尾数位（隐含一个1，总有效位为53）

格式化的值

当exp的位模式既不全为0，也不全为1时。

• 阶码字段E 被解释为以偏置(biased)形势表示的有符号整数，也就是说 $E = \exp - Bias$ ，$Bias = 2^{k-1} - 1$ ，k为exp的位数。由此产生的指数的范围，对于单精度为 -126 ~ +127，双精度为：-1022 ~ +1023
• 而frac被 解释为描述小数值f ，$0 \leq f < 1$ 。而 尾数 M = 1 + f 。

非格式化的值

当阶码（exp）全为0时，所表示的数是非格式化形式。

• E = 1 - Bias
• M = f (不包括隐含开头的1)

特殊值

阶码（exp）全为1时。

• s = 0 , 表示正无穷
• s = 1 ，表示负无穷

当小数域（frac）非零时，结果值被称为“NaN”表示不是一个数。

特殊问题(各类数值转化)

float f == (float)(double)f 吗？

c - Why is the statement "f == (float)(double)f;" wrong? - Stack Overflow

舍入

向偶舍入

向偶舍入大致于四舍五入相同，不过对于中间值的舍入该变了一点规则，就是舍入之后追求偶数，即1.5 舍入为2，2.5也舍入为2，但是除了.5，其他小数舍入于四舍五入相同。向偶舍入(round-to-even) , 也被称为向最接近的值舍入(round-to-nearest) , 是默认的方式。

其他三种舍入方法名字就能直观表示，请直接看图：

c语言中的浮点数

不幸的是，因为C语言标准不要求机器使用 IEEE浮点，所以没有标准的方法来改变舍入方式或者得到诸如-0、+～、-～或者 NaN之类的特殊值。